Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Zinsrechnung

zurück zur Seite der Herta-Lebenstein-Realschule

SEITE IM AUFBAU

1) Wiederholung der Grundbegriffe: Grundwert G, Prozentwert W und Prozentsatz p%
2) Vermehrter und verminderter Grundwert
3) Zinsrechnung

4) Monats- und Tageszinsen

3) Zinsrechnung

3.1 Grundbegriffe der Zinsrechnung

Idee

Zinsen - Wo und in welchem Zusammenhang hast du diesen Begriff schon einmal gehört? Notiere Beispiele in dein Heft.

Info

Schau dir das folgende Video zum Thema Grundbegriffe: Zinsrechnung' an.

Übung 1

Bearbeite die folgenden Online-Übungen zu den Grundbegriffen der Zinsrechnung.

Wenn du Geld bei einer Bank anlegst, so zahlt die Bank dir Zinsen. Den Geldbetrag, den du der Bank zur Verfügung stellst, nennt man Kapital. Du kannst dir bei einer Bank auch Geld leihen. Die Bank legt dann einen bestimmten Zinssatz dafür fest, d.h. sie gibt an, wie viel Prozent des Kapitals du als Zinsen zahlen musst. Häufig bezieht sich der Zinssatz auf ein Jahr. Deshalb nennt man sie auch Jahreszinsen.

Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Ordne zu, welchen Begriffen der Prozentrechnung die folgenden Begriffe und Abkürzungen der Zinsrechnung entsprechen.

Grundwert G	Kapital	K
Prozentwert W	Zinsen	Z
Prozentsatz p%	Zinssatz	p%

Hefteintrag

Zinsformel: Z = K · p%
Das Formeldreieck
Du kennst das Formeldreieck bereits aus der Prozentrechnung. Es ist auch eine Hilfe für das Umstellen der Formeln für die Zinsrechnung. Zeichne das Formeldreieck in dein Heft.

Merke dir die Anordnung der Größen im Dreieck. Halte die gesuchte Größe mit dem Finger zu, dann erhältst du die zugehörige Formel. Notiere die drei Formeln in dein Heft. Kontrolliere die Lösung.

Merkspruch für die Zinsformel:

Übung 2

Bearbeite die folgenden LearningApps.

Übung 3

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

1
2

und auf der Seite realmath die folgende Übung

Übung 1 (realmath)

3.2 Zinsen Z berechnen

Erklärvideo

Schau dir das Video zu Zinsen Z berechnen an.

Zinsen Z berechnen: Beispiel

Samuel hat zu Beginn des Jahres 620€ auf seinem Sparbuch.
Der Zinssatz der Bank beträgt 1,5%.

Übertrage die Aufgabe in dein Heft und berechne die Zinsen (mit Formel und Dreisatz).

gegeben: K = 620€; p% = 1,5% = 0,015
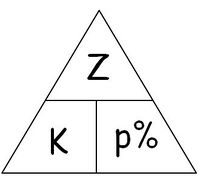
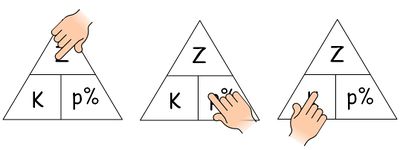
gesucht: Z
Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
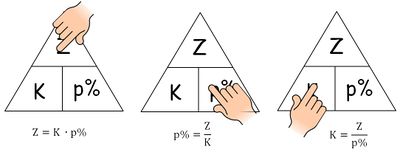
Z = K ⋅ p%

Übertrage folgende Tabelle in dein Heft und fülle sie aus.

%	€
100%	______
1%	______
______	______

|2=Tipps zur Berechnung mit Dreisatz|3=Verbergen

Übung 4

Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.

Übung 5

Bearbeite die folgende Aufgabe im Buch:

S. 110, Nr. 1

Schreibweise:
geg: K = 400€; p% = 2% = 0,02
ges: Z

Z = K ∙ p% |:G
Z = 400 ∙ 0,02
= 8 [€]

neuer Kontostand:
400€ + 8€ = 408€

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 1 bunt gemischt: Höhe der Zinsen

6,88€; 8€; 9,75€; 10,56€
Denke daran, auch den neuen Kontostand zu berechnen, d.h. Kapital + Zinsen.

Übung 6

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

4 - 9

und auf der Seite realmath die folgenden Übungen

3.3 Kapital K berechnen

Erklärvideo

Schau dir das Video zu Kapital K berechnen an.

Kapital K berechnen: Beispiel

Nach einem Jahr hat Anna für ihr Guthaben auf der Bank 18,90€ Zinsen erhalten.
Der Zinssatz beträgt 2,1%.

Übertrage die Aufgabe in dein Heft und berechne das Kapital (mit Formel und Dreisatz).

gegeben: Z = 18,90€; p% = 2,1% = 0,021
gesucht: K
Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle K = {Z \over p%}}

Übertrage folgende Tabelle in dein Heft und fülle sie aus.

%	€
2,1%	______
1%	______
______	______

|2=Tipps zur Berechnung mit Dreisatz|3=Verbergen

Übung 7

Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.

Übung 8

Bearbeite die folgende Aufgabe im Buch:

S. 110, Nr. 2

Schreibweise:
geg: p% = 7% = 0,07; Z = 560,00€
ges: K

K = $\tfrac{Z}{p%}$
K = $\tfrac{560}{0,07}$

= 8000 [€]

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 2 bunt gemischt:

5000€; 8000€;

\approx

1110,64€;

\approx

1295,45€

Übung 9

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

16 - 21

und auf der Seite realmath die folgenden Übungen

3.4 Zinssatz p% berechnen

Erklärvideo

Schau dir das Video zu Zinssatz p% berechnen an.

Zinssatz p% berechnen: Beispiel

Frau Koch hat sich von der Bank 4000€ geliehen. Hierfür muss sie der Bank 208€ Zinsen bezahlen.
Wie hoch ist der Zinssatz?

Übertrage die Aufgabe in dein Heft und berechne den Zinssatz (mit Formel und Dreisatz).

gegeben: Z = 208€; K = 4000€
gesucht: p%
Suche dir mithilfe des Formeldreiecks die passende Formel. Notiere sie, setze die Werte ein und berechne.
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle p% = {Z \over K}}

Übertrage folgende Tabelle in dein Heft und fülle sie aus.

€	%
4000€	______
4€	______
______	______

|2=Tipps zur Berechnung mit Dreisatz|3=Verbergen

Übung 10

Bearbeite die folgende Aufgabe aus der LearningApp im Heft und kontrolliere die Lösung mithilfe der App.

Übung 11

Bearbeite die folgende Aufgabe im Buch:

S. 110, Nr. 3

Schreibweise:
geg: K = 4800€; Z = 288,00€
ges: p%

p% = $\tfrac{Z}{K}$
p% = $\tfrac{288}{4800}$

= 0,06 = 6%

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 3 bunt gemischt:

4,9%; 6%; 6,77%, 7,8%

Übung 12

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

10 - 15

und auf der Seite realmath die folgende Übung

3.5 gemischte Übungen

Übung 13

Bearbeite die folgenden LearningApps.

Übung 14

Bearbeite die folgenden Aufgaben im Buch:

S. 110, Nr. 4, 5, 6, 7

Stelle drei verschiedene Rechnungen auf, um für jede Bank den entsprechenden Zinssatz zu berechnen.
K = 5000€ bleibt immer gleich. Die Zinsen Z betragen bei bei

Bank 1: 212,50€
Bank 2: 150€
Bank 3: 120€

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 4:

4,25%; 3%; 2,4%

geg.: K= 500€, p%= 1,75% = 0,0175

ges.: Z

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 5:

8,75€

Stelle vier verschiedene Rechnungen auf, um für jede Person das Kapital zu berechnen, was sie zu Beginn des Jahres angelegt hat.
p% = 1,5% = 0,015 bleibt immer gleich. Die Zinsen Z betragen bei

S: 6€
M: 4,50€
H: 7,50€
T: 11,37€

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 6:

400€; 300€; 500€; 758€

Hier hast du ein "vermehrtes Kapital" = K+ vorliegen und auch dementsprechend den "vermehrten Zinssatz" = p+%. Versuche dein Wissen aus der Prozentrechnung zum vermehrten Grundwert hier anzuwenden. Wenn du nicht weiterkommst, schaue dir Tipp 2 an.

K+ = 2000€
p+% = 100% + 1,75% = 101,75% = 1,0175.

Verwende die Formel: K+ = K ∙ p+%.
Stelle sie nach K hin um, setze die Werte ein und berechne.

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 7:

1965,60€

Übung 15

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

22 - 30

und auf der Seite realmath die folgende Übung

Angebote vergleichen

Berechne für beide Angebote den jeweiligen Zinssatz p%.

Bank 2 bietet mit einem Zinssatz von 5% ein besseres Angebot. Bank 1 bietet den Kredit mit einem Zinssatz von 5,5% an.

Übung 16: Angebote vergleichen

Bearbeite die folgenden Aufgaben im Buch:

S. 111, Nr. 9, 10

zu a) Vergleiche die Höhe der Zinssätze und des Kapitals. Gibt es zusätzlich feste oder abhängige Gebühren?
zu b) Berechne für beide Angebote die Zinsen. Bei Angebot 2 musst du zusätzlich ebenfalls die Höhe der Bearbeitungsgebühr berechnen. Addiere anschließend die jeweiligen Zinsen und Bearbeitungsgebühren zu dem entsprechenden Angebot. Bei welchem Angebot muss man weniger zurückzahlen?

Bei dem ersten Angebot muss man 11250€ und bei dem zweiten Angebot 11100€ zurückzahlen.

Berechne für alle drei Angebote den jeweiligen Zinssatz.

a) 9%; 8,75%, 8,5% (bunt gemischt)
b) Das Angebot der Bank mit dem geringsten Zinssatz ist am günstigsten.
c) Die Zinsen betragen 850€.

4) Monats- und Tageszinsen

Suche

Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Zinsrechnung

Inhaltsverzeichnis

3) Zinsrechnung

3.1 Grundbegriffe der Zinsrechnung

3.2 Zinsen Z berechnen

3.3 Kapital K berechnen

3.4 Zinssatz p% berechnen

3.5 gemischte Übungen

Navigation

Projekte

ZUM

Hilfen

Suche

Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Zinsrechnung

3) Zinsrechnung

3.1 Grundbegriffe der Zinsrechnung

3.2 Zinsen Z berechnen

3.3 Kapital K berechnen

3.4 Zinssatz p% berechnen

3.5 gemischte Übungen

Navigation

⧼timis-pagehighlighted⧽

⧼timis-pagenamespaces⧽

⧼timis-pagetranslate⧽

Seitenwerkzeuge

Seitenwerkzeuge