Benutzer:Buss-Haskert/Prozent-und Zinsrechnung/Zinsrechnung

Prozent-und Zinsrechnung Startseite

1) Wiederholung der Grundbegriffe: Grundwert G, Prozentwert W und Prozentsatz p%
2) Vermehrter und verminderter Grundwert

3) Zinsrechnung

3) Zinsrechnung

3.1 Grundbegriffe der Zinsrechnung

Idee

Zinsen - Wo und in welchem Zusammenhang hast du diesen Begriff schon einmal gehört? Notiere Beispiele in dein Heft.

Info

Schau dir das folgende Video zum Thema Grundbegriffe: Zinsrechnung' an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1

Bearbeite die folgenden Online-Übungen zu den Grundbegriffen der Zinsrechnung.

Wenn du Geld bei einer Bank anlegst, so zahlt die Bank dir Zinsen. Den Geldbetrag, den du der Bank zur Verfügung stellst, nennt man Kapital. Du kannst dir bei einer Bank auch Geld leihen. Die Bank legt dann einen bestimmten Zinssatz dafür fest, d.h. sie gibt an, wie viel Prozent des Kapitals du als Zinsen zahlen musst. Häufig bezieht sich der Zinssatz auf ein Jahr. Deshalb nennt man sie auch Jahreszinsen.

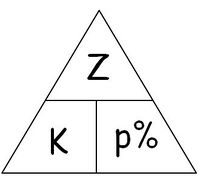
Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Ordne zu, welchen Begriffen der Prozentrechnung die folgenden Begriffe und Abkürzungen der Zinsrechnung entsprechen.

Grundwert G	Kapital	K
Prozentwert W	Zinsen	Z
Prozentsatz p%	Zinssatz	p%

Hefteintrag

Das Formeldreieck
Du kennst das Formeldreieck bereits aus der Prozentrechnung. Es ist auch eine Hilfe für das Umstellen der Formeln für die Zinsrechnung. Zeichne das Formeldreieck in dein Heft.

Merke dir die Anordnung der Größen im Dreieck. Halte die gesuchte Größe mit dem Finger zu, dann erhältst du die zugehörige Formel. Notiere die drei Formeln in dein Heft. Kontrolliere die Lösung.

Übung 2

Bearbeite die folgenden LearningApps.

Übung 3

Bearbeite auf der Seite Aufgabenfuchs die Aufgaben

• 1, 2

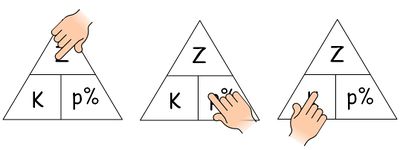
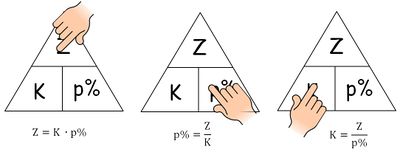
3.2 Zinsen Z berechnen

Zinsen Z berechnen: Formel und Dreisatz

Übertrage das Beispiel in dein Heft.

Übung 4

Bearbeite die folgende Aufgabe im Buch:

• S. 110, Nr. 1

Schreibweise:
geg: K = 400€; p% = 2% = 0,02
ges: Z

Z = K ∙ p%   |:G
Z = 400 ∙ 0,02
    = 8 [€]

neuer Kontostand:
400€ + 8€ = 408€

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 1 bunt gemischt: Höhe der Zinsen

6,88€; 8€; 9,75€; 10,56€
Denke daran, auch den neuen Kontostand zu berechnen, d.h. Kapital + Zinsen.

3.3 Kapital K berechnen

Kapital K berechnen: Formel und Dreisatz

Übertrage das Beispiel in dein Heft.

Übung 5

Bearbeite die folgende Aufgabe im Buch:

• S. 110, Nr. 2

Schreibweise:
geg: p% = 7% = 0,07; Z = 560,00€
ges: K

K = $\tfrac{Z}{p$
K = $\tfrac{560}{0,07}$

    = 8000 [€]

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 2 bunt gemischt:

5000€; 8000€; $\approx$1110,64€; $\approx$1295,45€

3.4 Zinssatz p% berechnen

Zinssatz p% berechnen: Formel und Dreisatz

Übertrage das Beispiel in dein Heft.

Übung 6

Bearbeite die folgende Aufgabe im Buch:

• S. 110, Nr. 3

Schreibweise:
geg: K = 4800€; Z = 288,00€
ges: p%

p% = $\tfrac{Z}{K}$
p% = $\tfrac{288}{4800}$

    = 0,06 = 6%

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 3 bunt gemischt:

4,9%; 6%; 6,77%, 7,8%

3.5 gemischte Übungen

Übung 7

Bearbeite die folgenden LearningApps.

Übung 8

Bearbeite die folgenden Aufgaben im Buch:

• S. 110, Nr. 4, 5, 6, 7

Stelle drei verschiedene Rechnungen auf, um für jede Bank den entsprechenden Zinssatz zu berechnen.
K = 5000€ bleibt immer gleich. Die Zinsen Z betragen bei bei

• Bank 1: 212,50€
• Bank 2: 150€
• Bank 3: 120€.

Tipp zu Nr. 4

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 4:

4,25%; 3%; 2,4%

geg.: K, p%

ges.: Z

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 5:

8,75€

Tipp zu Nr. 6

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösungen zu Nr. 6:

400€; 300€; 500€; 758€

...€

Vergleiche deine Lösungen mit einem andersfarbigen Stift!
Lösung zu Nr. 7:

1965,60€

4) Monats- und Tageszinsen