Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme
In diesem Kapitel kannst du etwas zum Thema Optimierungsprobleme lernen.
In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.
Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.
Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
In diesem Kapitel erklären wir dir zunächst, was Optimierungsprobleme sind. Dabei werden wir wichtige Begriffe wiederholen.
Anschließend kannst du selbstständig Aufgaben bearbeiten.
Viel Erfolg!
Inhaltsverzeichnis
Einführung: Optimierungsprobleme
Optimierungsprobleme , oder auch Extremwertprobleme, beschreiben eine Aufgabenform, bei der nach dem optimalen Wert einer Funktion gefragt wird. Dieser optimale Wert ist oftmals ein Extremwert, also ein Maximum oder ein Minimum.
Die Berechnung erfolgt dabei im Sachzusammenhang, es wird also beispielsweise nach dem minimalen Volumen einer Schachtel gefragt, die man mit einem Blatt Papier falten kann, oder nach dem maximalen Flächeninhalt eines Grundstücks, das man mit einer bestimmten Meterzahl an Zaunteilen einzäunen kann.
Die Funktion, deren Extremwert es zu bestimmen gilt, muss also noch ermittelt werden.Vorgehen beim Lösen von Optimierungsproblemen
Bei Optimierungsproblemen geht es stets darum, dass eine bestimmte Größe optimiert werden soll. So wird z. B. eine optimale Verpackung für Reis oder die optimale Anzahl an Zahnpasten gesucht, die in einen Karton passen - es geht also um eine Anwendungssituation. Das Ergebnis eines Optimierungsproblems ist daher auch meist kein exakter Wert sondern ein Näherungswert. Dieser muss natürlich sinnvoll gewählt sein.
Zur Lösung eines Optimierungsproblems muss man zunächst die Aufgabe genau lesen und verstehen. Hierbei kann man sich die folgenden Fragen stellen: Worum geht es? Welche Größen kommen vor und wie hängen sie zusammen? Welche Größe soll nun optimiert, also maximiert oder minimiert werden?
Der optimale Wert bedeutet mathematisch, den Extremwert einer Funktion zu bestimmen. Du musst also das Optimierungsproblem als Funktion ausdrücken und dabei die anderen Größen miteinbeziehen. Mit dieser Funktion kannst du dann den optimalen Wert bestimmen.
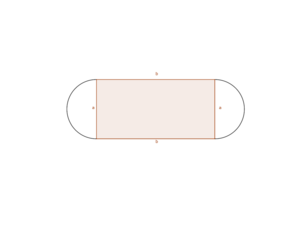
Ein Sportplatz mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. Die seitlichen Kurven des Sportplatzes sollen Halbkreise sein.
a) Für welche Länge und für weiche Breite wird das Fußballfeld im Inneren des Sportplatzes maximal?
b) Wie groß ist das Fußballfeld?
Gegeben ist die Länge der Laufbahn um den Sportplatz herum, also der Umfang des Sportplatzes. Maximiert werden soll die Größe des Fussballfeldes, also der rechteckige Flächeninhalt innerhalb des Sportplatzes. Überlege also zunächst, wie der Flächeninhalt
berechnet wird.
Über die Größen selbst weißt du ebenfalls etwas durch den Umfang: . Stelle die Formel für den Umfang nun nach
um.
Setze nun deine Formel für in den Flächeninhalt ein. So erhälst du deine Zielfunktion.
Deine Zielfunktion ist:
Für die Zielfunktion kann nur zwischen
und
liegen, also
Nun musst du den optimalen Wert berechnen. Gesucht ist hier das Maximum. Bilde dazu die Ableitungen:
Prüfe nun die notwendige und hinreichende Bedingung.
Mit der notwendigen Bedingung erhälst du dann
.
Berechne nun .
Berechne nun durch Einsetzen von und
den Flächeninhalt
:
Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen () her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein:
- Die Länge (
) soll nicht größer als
sein.
- Länge (
) plus Umfang einer quadratischen Seitenfläche soll
groß sein.
a) Ermittle die Abmessungen des Pakets mit dem größten Volumen.
b) Gebe das maximale Volumen an.
Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach um.
Die Definitionsmenge für die Zielfunktion ergibt sich aus der Bedingung für die Länge (
).
Die Länge muss zum einen größer gleich
und zum anderen kleiner gleich
sein. Also gelten die folgenden zwei Ungleichungen, die du einfach nach a auflösen kannst.
und
Zielfunktion aufstellen: Um das Volumen des Paktes zu errechnen, verwenden wir die folgende Funktion, die von den Variablen und
abgängig ist:
.
Nebenbedingung aufstellen: Durch die zweite Bedingung können wir die folgende Gleichung aufstellen.
.
Die Gleichung stellen wir nach
um und erhalten:
.
Nun können wir
in die Zielfunktion
einsetzen, welche dann durch noch von der Variable
abhängt. Wir schreiben dann für die Funktion
und erhalten
.
Definitionsmenge angeben: Wir wollen nun eine Definitionsmenge für die Funktion angeben. Diese erhalten wir, indem wir uns die Bedingung für die Länge (
) anschauen.
Offensichtlich muss die Länge größer gleich
sein. Es gilt also:
.
Durch das Umstellen nach
folgt:
.
Außerdem muss die Länger kleiner gleich
sein. Es gilt also:
<
.
Durch das Umstellen nach
folgt:
.
Insgesamt ergibt das also
.
Nun sollen die Extremstellen von bestimmt werden.
.
Notw. Bedingung: .
(Klammere das
aus und wende den Satz vom Nullprodukt an. Alternativ kannst du auch die pq-Formel anwenden)
oder
.
Da
muss
gelten, also
.
Durch das Einsetzen von in
folgt, dass
an dieser Stelle einen Hochpunkt besitzt.
Breite und Höhe sind also .
Die Länge ergibt sich durch das einsetzen von
in
.
.
Das Volumen bestimmen: Wir berechnen nun das Volumen des optimalen Paketes, indem wir berechnen.
Leon möchte aus einem kreisförmigen Stück Papier mit dem Radius eine Pommestüte formen.
Dazu schneidet er den Kreis längs eines Radius ein. Nun versucht Leon die Pommestüte so zu formen, sodass das Volumen der Pommestüte maximal ist, damit auch möglichst viele Pommes hineinpassen.
Was ist das maximale Volumen der Pommestüte?Leon möchte aus einem kreisförmigen Stück Papier eine Pommestüte formen, in der möglichst viele Pommes hineinpassen. Zu optimieren ist also das Volumen der Pommestüte.
Rollt Leon das Stück Papier nicht, so ist ist das Volumen . Rollte Leon das Stück Papier ganz zusammen, so ist
.
Gegeben ist die Mantellinie mit der Pommestüte. Außerdem ist das Volumen der Pommestüte von den Variablen
(Radius) und
(Höhe) abhängig. Mit dem Satz des Pythagoras ergibt sich
. Stelle diese Gleichung nun nach
um und erhalte
.
Setze diesen Ausdruck nun für in die Formel für das Volumen ein. Du erhälst folgende Zielfunktion:
.
Für diese Funktion kann nur zwischen
und
liegen, also
.
Da es sich um eine Anwendungssituation handelt, reicht ein guter Näherungswert.
Die Ableitungsfunktion lautet .
Globales Extremum und Randextremum
Der größte Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Maximum. Der kleinste Funktionswert unter allen Funktionswerten in der Definitionsmenge heißt globales Minimum.
Ein globales Extremum an einer Randstelle der Definitionsmenge heißt Randextremum.
Gegeben ist der Graph einer Funktion mit
im Intervall
.
Ein achsenparalleles Rechteck wird so gelegt, dass ein Eckpunkt der Koordinatenursprung ist und der gegenüberliegende Eckpunkt auf dem Graphen von g liegt.
Welches der möglichen Rechtecke hat den größten Flächeninhalt?

Mit in
berechnen wir den Flächeninhalt mit der Funktion
.
Die Nebenbedingung ist die angegebene Funktion .
Setzt man nun die Nebenbedingung in die Funktion ein, so erhalten wir
. Die Funktion heißt nun
, da sie nur noch von der Unbekannte
abhängt.
Nun lässt sich mit Hilfe der notwendigen Bedingung und der hinreichenden Bedingung für Hochpunkte
die Stelle des lokalen Hochpunktes bestimmen. Anschließend setzen wir
in die Ausgangsfunktion
ein und erhalten nun den lokalen Hochpunkt
.
Zuletzt prüfen wir noch die Randpunkte.
und
.
Damit liegt der globale Hochpunkt an der Stelle .
Optimierungsprobleme & Funktionenscharen
In bestimmten Fällen kann es vorkommen, dass die erhaltene Funktion nicht nur von einer Variable abhängt, sondern außerdem von einem Parameter
.
Gegeben ist die Funktionenschar .
Für welchen Wert von liegt der Tiefpunkt der Funktionenschar am höchsten?
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von .
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und
.
Minimum
Setze nun in
ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
Die zu optimierende Größe ist der Funktionswert am Tiefpunkt der Funktion.
Berechne also zunächst den Tiefpunkt der Funktion in Abhängigkeit von :
Ableiten der Funktion ergibt:
Für ein Minimum muss gelten: und
.
Minimum
Setze nun in
ein, um den Funktionswert am Minimum zu bestimmen:
Bezeichnen wir den Funktionswert am Tiefpunkt mit einer neuen Gleichung , so ergibt sich also:
.
Gesucht ist das , für das der Funktionswert maximal ist, also das Maximum der Funktion
.
Bilde zunächst wieder die Ableitungen und
:
Bei einem Maximum muss gelten: und
.
Maximum