Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Änderungsrate zum Änderungseffekt
Als Einstieg in das Kapitel findest du eine Herleitung des Integrals aus dem Kontext der Differentialrechnung. Dabei werden dir die zwei Oberbegriffe des Kapitels Änderungsrate und Änderungseffekt erläutert. Anschließend folgen einige Aufgaben zum Integral. Die Aufgaben werden in drei unterschiedliche Schwierigkeitsstufen eingeteilt so dass du jederzeit die Möglichkeit hast auf deinem Leistungsstand zu arbeiten.
In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.
Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit. Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.Inhaltsverzeichnis
Herleitung des Integrals
Konstante und lineare Funktionen
Wir nehmen an, dass ein Jogger im Durchschnitt 3m/s läuft. Dadurch ergibt sich die konstante Funktion , wie in der unteren Abbildung dargestellt. Nun kann man sich die Frage stellen: Wie viel Meter hat er in einer bestimmten Zeit zurückgelegt? Um das herauszufinden, muss lediglich der Flächeninhalt des Rechtecks zwischen dem Graphen f(x) und der x-Achse in einem festgelegten Zeitintervall berechnet werden. Beispielsweise hätte der Jogger innerhalb der ersten 10s eine Strecke von 30m (
) zurückgelegt. Das lässt sich für beliebig große Intervalle
auf der x-Achse fortführen.
Probiere das in der Darstellung aus indem du die Grenze b verschiebst. Vergleiche den Wert der Stammfunktion F(x) mit dem Wert des Flächeninhalts. Was fällt dir auf?

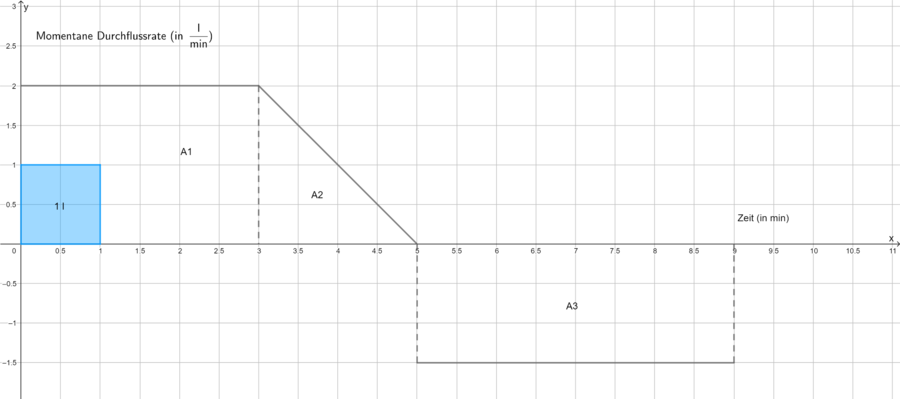
Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur 1 ist die momentane Durchflussrate f der Leitung für das Intervall dargestellt.
Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank?
Im Intervall beträgt der Zufluss
. In diesen 3 Minuten fließen
in den Tank. Im Intervall
beträgt die mittlere Zuflussrate
. In diesen 2 Minuten kommen
dazu. Im Intevall
ist die Durchflussrate negativ. Es fließen
ab. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall
mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser orientierte Flächeninhalt beträgt beim Wassertank:
Allgemeine Herleitung und Definition
Bei konstanten oder linearen Funktionen schafft man es den Änderungseffekt durch Rechtecks- und Dreicksflächen zu ermitteln. Doch wie funktioniert das bei Funktionen zweiten Grades oder höher?
Um den Effekt bei Funktionen zweiten Grades oder höher zu ermitteln nutzt man dasselbe Verfahren. Man versucht sich der Fläche zwischen dem Graphen und der x-Achse mit Rechtecksflächen anzunähern. Aktiviere dazu in der unteren Abbildung die Untersumme. Für einen direkten Vergleich kannst du auch das Integral aktivieren.
Hinweise:
- N markiert die Anzahl der Rechtecke unter dem Graphen.
- Das Δx gibt die Breite der Rechtecke an. Je mehr Rechtecke unterhalb des Graphen desto kleiner wird ihre Breite und damit auch das Δx.
- Die eingeblendete Untersumme gibt den aktuellen Flächeninhalt der Summe aller Rechtecksflächen an.

- Je mehr Unterteilungen desto kleiner wird die Breite der Rechtecke.
- Je mehr Unterteilungen der Untersumme desto größer wird der Flächeninhalt der Summe aller Rechtecke.
- Die Summenformel der Untersumme stellt den Flächeninhalt aller Rechtecke dar.
- Je mehr Unterteilungen und je kleiner das Δx desto eher nähert man sich dem Integral. Geht also die Anzahl der Unterteilungen gegen unendlich so bekommt man das Integral für die Funktion über das jeweilige Intervall.
Die Funktion sei auf dem Intervall
stetig (Graph kann nahtlos gezeichnet werden) und
sei eine beliebige Rechtecksumme zu
über dem Intervall
.
Dann heißt der Grenzwert Integral der Funktion
zwischen den Grenzen
und
.
Man schreibt dafür:
Die Funktion sei stetig (Graph kann nahtlos gezeichnet werden) auf dem Intervall
. Dann gilt:
Stammfunktionen bilden
Eine Funktion heißt Stammfunktion zu einer Funktion
auf einem Intervall
, wenn für alle
in
gilt:
.
Sind
und
Stammfunktionen von
auf einem Intervall
, dann gibt es eine Konstante
, sodass für alle
in
gilt:
Zur Funktion mit
ist
mit
eine Stammfunktion.
Zur Funktion
mit
ist
mit
eine Stammfunktion.
Sind
und
Stammfunktionen von
und
, so gilt für die zusammengesetzten Funktionen:
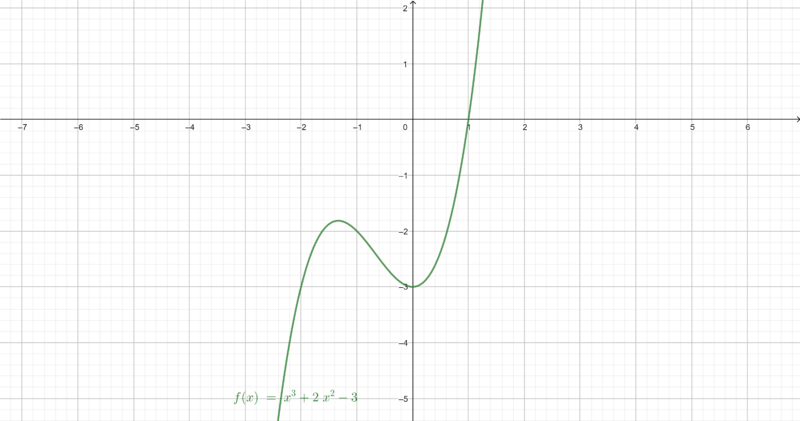
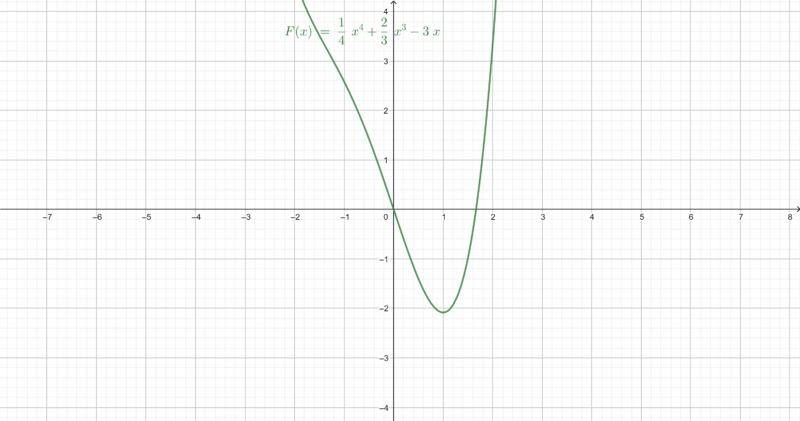
Hier findest du ein paar Beispiel Funktionen und ihre Stammfunktion.
Gelerntes Wiederholen und Vertiefen
Du erkennst, dass der orientierte Flächeninhalt nicht mit dem Wert des Flächeninhalts zwischen Graph und x-Achse übereinstimmt. Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten.
Du kannst die App oben in der rechten Ecke in den Vollbildmodus schalten, damit du alles besser erkennen kannst. Du sollst in der Aufgabe zu jeder Funktion (insgesamt 4 Funktionen) den dargestellten Flächeninhalt A und das entsprechende Integral I zuordnen. Dies machst du, indem du die vorgegebenen Lösungen über das Feld, wo die entsprechende Funktion abgebildet ist, ziehst. Am Ende kannst du überprüfen, ob du alles richtig zugeordnet hast.
- Für den Flächeninhalt A solltet ihr den Flächeninhalt der einzelnen Formen (Rechteck oder Dreieck) bestimmen und anschließend die Flächeninhalte aller addieren.
- Gibt es Rechtecke oder Dreiecke, die die gleiche Form haben und gleich groß sind? Wenn du welche findest, heben sich diese eventuell gegenseitig auf? Dies ist der Fall wenn eine Form oberhalb der x-Achse ist und die zugehörige andere Form unterhalb der x-Achse. Dann wäre das Integral der beiden Formen 0.
- Beachte, dass das Integral I maximal der Flächeninhalt A d.h.
sein kann. Dies kann nur der Fall sein, sofern die Funktion komplett oberhalb der x-Achse verläuft.
- Das Integral I kann auch negativ sein, sofern die Fläche, die zwischen Graph und unterhalb der x-Achse ist, größer als die Fläche, die zwischen Graph und oberhalb der x-Achse ist.
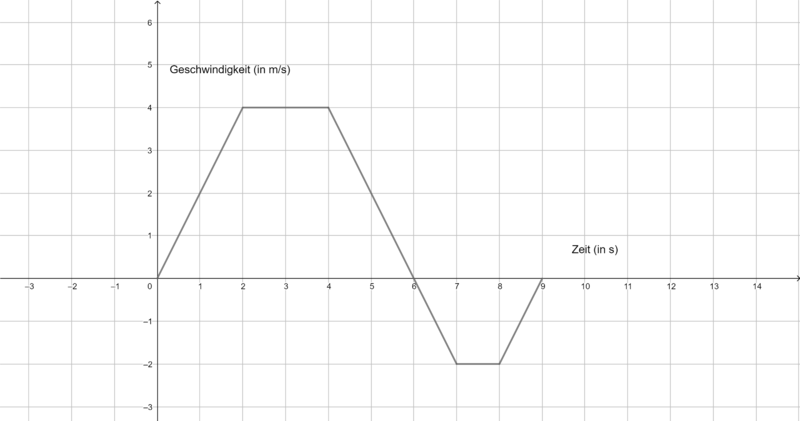
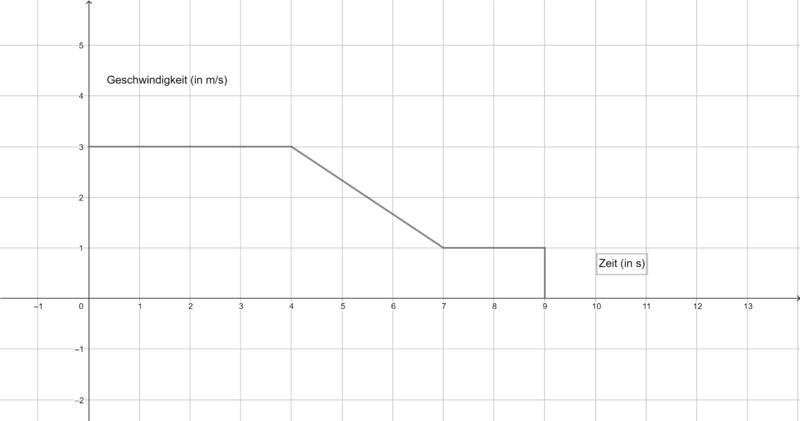
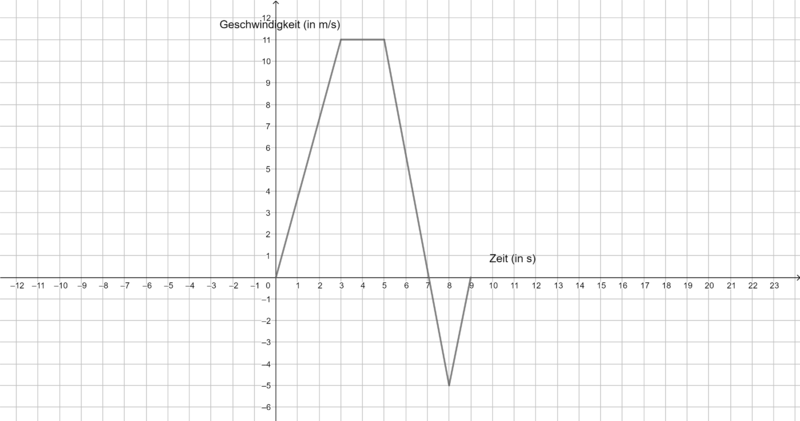
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittle jeweils die vom Startpunkt zurückgelegte Strecke in m nach 9 s. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse zu notieren.
a)- Fläche oberhalb der x-Achse:
- Flächer unterhalb der x-Achse:
- Integral/orientierter Flächeninhalt:
- Der Körper hat eine Strecke von 12 m vom Startpunkt zurückgelegt.
- Fläche oberhalb der x-Achse:
- Flächer unterhalb der x-Achse:
- Integral/orientierter Flächeninhalt:
- Der Körper hat eine Strecke von 20 m vom Startpunkt zurückgelegt.
- Fläche oberhalb der x-Achse:
- Flächer unterhalb der x-Achse:
- Integral/orientierter Flächeninhalt:
- Der Körper hat eine Strecke von 44,5 m vom Startpunkt zurückgelegt.
Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden.

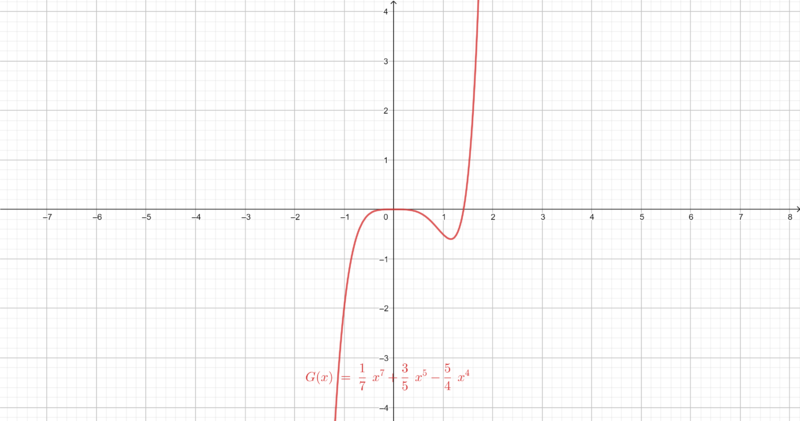
Bearbeite die folgenden Aufgabe. Ordne die Graphen der Funktion mithilfe von charakteristischen Punkten den Graphen der Stammfunktion
zu. Falls du Schwierigkeiten mit der Zuordnung hast, schaue dir Aufgabe 3 an?
Auch hier kannst du den Vollbildmodus in der rechten, oberen Ecke einschalten, sodass du die Graphen der entsprechenden Funktionen besser erkennen kannst.
- Mache dir klar, wie die Funktion f und eine zugehörige Stammfunktion F zueinander stehen. Was bedeutet es, dass F eine Stammfunktion von f ist.
- Was gilt für die Stammfunktion F von f, wenn f an der Stelle a einen lokalen Wendepunkt oder ein lokales Maximum bzw. lokales Minimum besitzt?
- f(x) ist die Ableitung von F(x). Somit gibt die Funktion f die Steigung der Stammfunktion F an.
- Hat F an der Stelle a einen lokalen Wendepunkt (d.h. lokale maximale bzw. lokale minimale Steigung), so hat f an der Stelle a ein lokales Maximum bzw. ein lokales Minimum.
- Hat F an der Stelle a ein lokales Maximum bzw. ein lokales Minimum, so hat f an der Stelle a einen lokalen Wendepunkt.
Aufgaben mittlerer Schwierigkeit
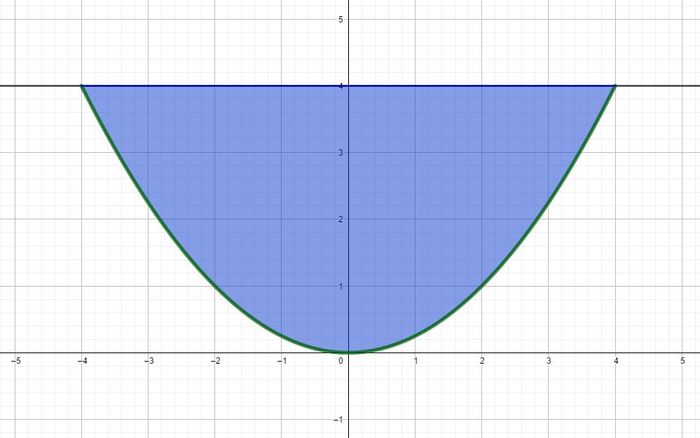
Der Boden eines 2 km langen Kanals hat die Form einer Parabel (siehe Abbildung). Dabei entspricht eine Längeneinheit 1 m in der Wirklichkeit.
a)
Gib den Inhalt der Querschnittsfläche A des Kanals an. Nimm dabei an, dass die Funktion f mit den Grundverlauf des Kanals darstellt.
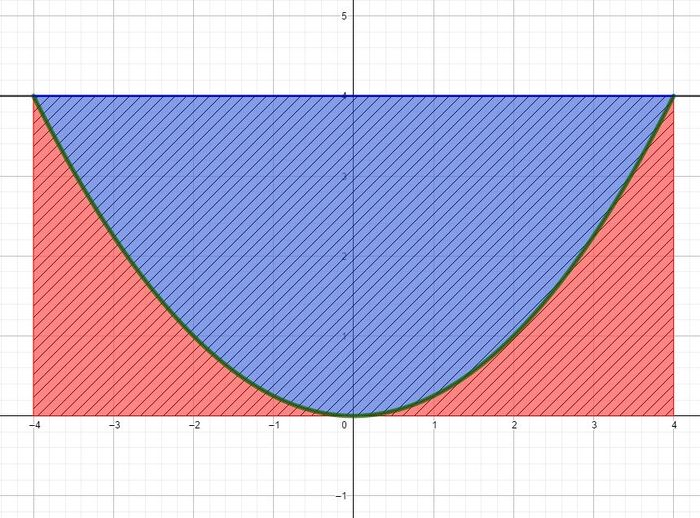
Es gibt mehrere Möglichkeiten, um den Inhalt der Querschnittsfläche des Kanal zu berechnen. Im folgenden werden 3 Möglichkeiten aufgeführt.
- Du berechnest das Integral von der Funktion f mit den Grenzen
. Weiter berechnest du den Flächeninhalt des Rechtecks (schraffiert, siehe nachfolgende Abbildung). Abschließend subtrahierst du die Fläche des Integrals (Rot) von der des Rechtecks.
- Du erstellst eine zweite Funktion
, welche den Wasserstand im Kanal wiederspiegelt. Die Fläche unterhalb des Graphen (das Integral) g mit den Grenzen
entspricht dem Flächeninhalt des Rechtecks aus Möglichkeit 1. Nun kannst du wie in Möglichkeit 1 vorgehen. Du kannst aber auch das Integral von
mit den Grenzen
, also
berechnen, was der gleichen Fläche entspricht.
- Du verschiebst die Funktion um 4 Einheiten nach unten, sodass die x-Achse den Wasserspiegel entspricht. Anschließend berechnest du das Integral. Da dies negativ sein wird, musst du noch den Betrag davon nehmen.
und
b)
Wie viel Wasser [in ] befindet sich im Kanal, wenn er komplett gefüllt ist?
c) Wie viel Prozent der maximalen Wassermenge befindet sich im Kanal, wenn er nur halb gefüllt ist?
,
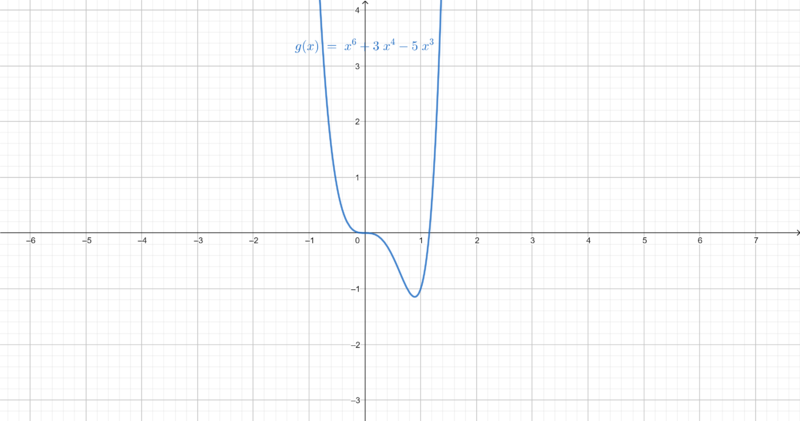
Skizziere eine beliebige Stammfunktion zu folgenden Funktionen auf dem Intervall . Zeichne zunächst die Funktion und dann die Stammfunktion in ein Koordinatensystem auf einen Zettel. Nutze charakteristische Punkte (Nullstellen, Extrempunkte, etc.), um den Graph der Stammfunktion zu zeichnen.
- Um eine Stammfunktion F zu einer Funktion f zu skizzieren, musst du dir klar sein, wie die Funktion f und eine zugehörige Stammfunktion F zueinander stehen. Was bedeutet es, dass F eine Stammfunktion von f ist.
- Was gilt für die Stammfunktion F von f, wenn f an der Stelle a einen lokalen Wendepunkt oder ein lokales Maximum bzw. lokales Minimum besitzt?
- Wenn dir der Zusammenhang klar ist, kannst du diese Punkte einzeichnen und hast schon einen groben "Rahmen" für deine zu skizzierende Stammfunktion.
- f(x) ist die Ableitung von F(x). Somit gibt die Funktion f die Steigung der Stammfunktion F an.
- Hat F an der Stelle a einen lokalen Wendepunkt (d.h. lokale maximale bzw. lokale minimale Steigung), so hat f an der Stelle a ein lokales Maximum bzw. ein lokales Minimum.
- Hat F an der Stelle a ein lokales Maximum bzw. ein lokales Minimum, so hat f an der Stelle a eine Nullstelle.
Ordne den Funktionen ihre passende Stammfunktion zu. Ermittle dabei die Stammfunktion auf einem Zettel und ordne anschließend richtig zu.
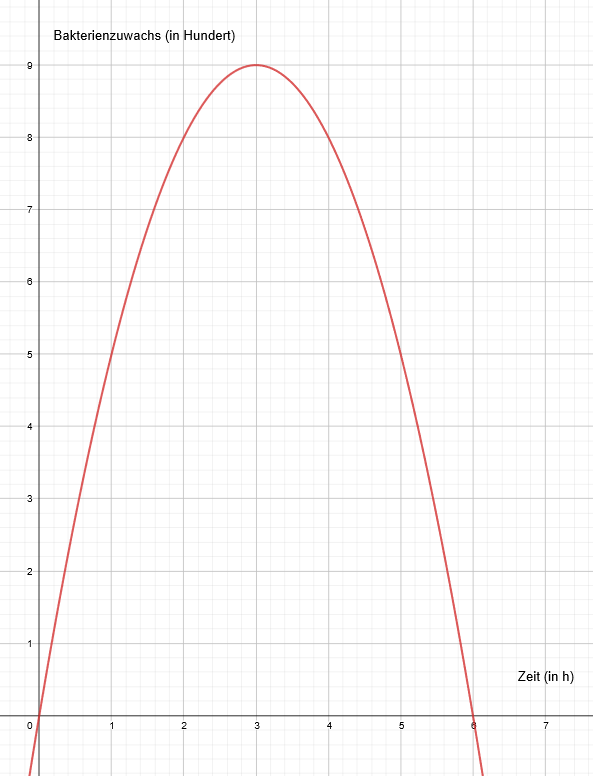
Die Funktion gibt die Wachstumsrate von Bakterien an,
in Stunden,
in Hundert Bakterien (siehe Figur 1). Zu Beginn waren 200 Bakterien vorhanden.
a) Wie lautet die Funktion , die die vorhandene Anzahl von Bakterien zum Zeitpunkt
angibt?
b) Wie viele Bakterien existieren nach 4 Stunden und nach 6 Stunden?
Knobelaufgaben
Die biologische Aktivität in einem Teich kann man durch die Änderungsrate beschreiben, mit der CO₂ dem Wasser zugefügt oder entnommen wird. Pflanzen entnehmen tagsüber dem Wasser im Rahmen der Photosynthese CO₂ und geben Nachts O₂ ab. Tiere geben durch ihre Atmung CO₂ an das Wasser ab. Bei Tagesanbruch werden 2,6ME CO₂ im Teich festgestellt. (ME steht hier für eine nicht so ganz gebräuchliche Mengen-Einheit, in der die Stoffmenge von CO₂ gemessen werden kann.) Biologen haben die Zu- und Abnahmerate über einen ganzen Tag, beginnend mit dem Sonnenaufgang, gemessen. Die Werte werden in der Einheit ME pro Stunde angegeben.
| Zeit t in h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| Änderungsrate z(t) in ME/h | 0,0 | -0,041 | -0,037 | -0,026 | -0,009 | 0,046 | 0,031 | 0,019 | 0,006 |
a) Begründe, dass der Teich Pflanzen enthält.
b) Berechne für jede der angegebenen Zeiten die Gesamtmenge von CO₂ im Wasser und stelle die Ergebnisse tabellarisch dar. Runde jedes Ergebnis auf zwei Nachkommastellen.
- Für
: Bei Tagesanbruch wurden 2,6 ME CO₂ im Teich gemessen (siehe Aufgabe).
- Für
: Wir betrachten die Fläche auf dem Intervall
. Die erste Seite des Dreiecks ist die Länge des Intervalls und beträgt 3. Die zweite Seite des Dreiecks ist der Punkt (3,-0,041) und damit -0,041. Daraus ergibt sich die folgende Gesamtmenge:
≈
(aufgerundet)
- Für
: Wir betrachten die Fläche
auf dem Intervall
. Den Flächeninhalt auf dem Intervall
kennen wir bereits als
. Die Fläche unter dem Graphen auf dem Intervall
besteht aus einer Vierecks- und einer Dreiecksfläche und wird wie folgt berechnet:
≈
(aufgerundet).
- Für
mit dem gleichen Verfahren.
| Zeit t in h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| Gesamtmenge CO₂ in ME | 2,6 | 2,54 | 2,42 | 2,33 | 2,28 | 2,33 | 2,45 | 2,53 | 2,57 |
c) Wann war der CO₂-Gehalt am niedrigsten? Wie groß war er?
d) Welche Bedeutung haben die folgenden Integrale für die vorgegebene Situation?
- Das Integral beschreibt die Durchschnittliche CO₂ Menge im Teich von morgens bis nach 12 Stunden. Die Fläche liegt unterhalb der x-Achse, also wurde im betreffenden Zeitraum mehr CO₂ entnommen als abgegeben, der Gesamtbestand ist gesunken.
- Das Integral beschreibt die Durchschnittliche CO₂ Menge im Teich von 12 bis nach 24 Stunden. Die Fläche liegt oberhalb der x-Achse, also wurde im betreffenden Zeitraum mehr CO₂ abgegeben als entnommen, der Gesamtbestand ist also gestiegen.
- Das Integral beschreibt die Durchschnittliche CO₂ Menge im Teich von morgens bis nach 24 Stunden. Das Integral gibt an, wie viel CO₂ nach 24 Stunden im Vergleich zum Anfangsbestand hinzugekommen ist bzw. entnommen wurde.
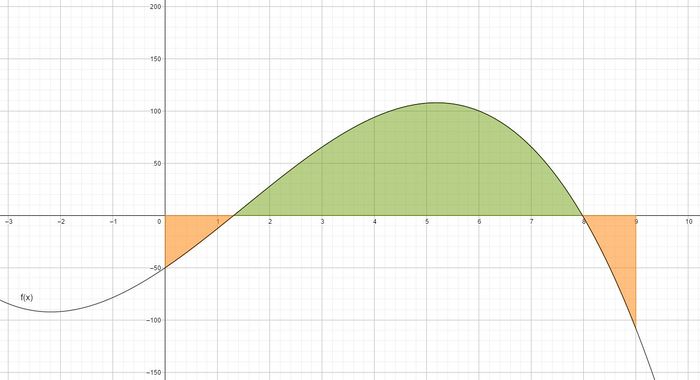
Ein Technik-Unternehmen hat ein neues Smartphone auf den Markt gebracht. Nach 9 Monaten will das Unternehmen prüfen, wie lukrativ das neue Handy in den ersten 9 Monaten war. Der monatliche Gewinn, der durch das Smartphone eingespielt wurde, kann durch die folgende Funktion dargestellt werden:
Die x-Achse gibt die Anzahl der Monate an und die y-Achse den Gewinn in Millionen (€).
a) Berechne den Ertrag, den das Unternehmen in den ersten 2 Monaten, 7 Monaten und nach den kompletten 9 Monaten durch das Smartphone eingespielt hat.
b) In welchem Zeitraum erbringt das Smartphone ausschließlich Gewinn für das Unternehmen? Wie viel wird in dem Zeitraum eingenommen?
c) Interpretiere die Ergebnisse aus der Aufgabe a) und überlege dir mögliche Begründungen für die erzielten Beträge. Sollte das Smartphone weiterhin produziert werden?
Hier sollst du dir Gedanken machen, ob einerseits deine Ergebnisse aus den vorherigen Aufgaben Sinn ergeben (solltest du natürlich nach jeder Aufgabe machen), und anschließend deine eigenen Begründungen der Ergebnisse festhalten. Zum Bespiel, könnte der anfängliche Verlust mit höheren Produktionskosten als Verkaufseinnahmen begründet werden (warum? plausible Begründung).
Zur Überlegung, ob es lukrativ ist, das Smartphone weiterhin zu produzieren, solltest du dir den Gewinn bzw. Verlust der gesamten 9 Monate anschauen und natürlich den Verlauf der Funktion, die die Einnahmen wiederspiegelt.
Bei einem Sprint über 100m treten Lars und René gegeneinander an. Lars sprintet mit der Geschwindigkeitsfunktion .
René sprintet mit der Geschwindigkeitsfunktion
.
ist jeweils die Zeit in Sekunden ab dem Start des Laufes und
die Geschwindigkeit
von Lars und René in Meter pro Sekunde.
a) Gib die Funktionen an, die die zurückgelegte Strecke zum Zeitpunkt angibt.
b) Zeige, dass Lars ungefähr 9,8 Sekunden benötigt.
c) Bestimme den Wert von r so, dass René nach 9,69 Sekunden ins Ziel kommt.
d) Wie viel Meter sind die Lars und René nach 5 s von einander entfernt, wenn r dem in c) ermittelten Wert entspricht?
Bei einer Coronavirusinfektion ergibt sich die Anzahl der Viren (in Milliarden) nach folgender Funktionsgleichung:
(x: Anzahl der Tage)
Wie bei fast allen Virusinfektionen vergeht auch beim derzeitg kursierenden Coronavirus eine gewisse Zeit von der Ansteckung bis zur Erkrankung (Inkubationszeit). Das Robert Koch-Institut schätzt die Inkubationszeit für SARS-CoV-2 auf 3-5 Tage.
Ein halbes Jahr später hat die Forschung das Medikament „Gibcovid19einenkorb“ entwickelt, um der Ausbreitung des Coronavirus entgegenzuwirken. Die Wirkung des Medikaments bzw. die Abnahme der Viren lässt sich mit folgender Funktion beschreiben:
Dieses Medikament kann erst nach 3 Tagen verabreicht werden, da dann die ersten Symptome auftreten können.
a) Ein Patient ist mit dem Coronavirus infiziert und bekommt nach 3 Tagen das Medikament verabreicht. Berechne nach wie vielen Tagen (x = a) alle Viren im Körper des Patienten abgestorben sind (Runde das Ergebnis sinnvoll).
Es handelt sich um eine aus zwei Teilfunktionen zusammengesetzte Funktion:
, für 0 ≤ x ≤ 3 und
, für 3 ≤ x ≤ a.
Bestimme die NST des zweiten Funktionsterms für x≥3:
↔
↔
Anwendung der p/q Formel:
,
≈
,
≈
<
b) Die Fläche zwischen dem Graphen und der x- Achse ist ein Maß für die schädigende Wirkung der Coronaviren, auch Wirkungsfaktor genannt. Gesundheitliche Schäden können auftreten, wenn der Wert 60 WE (Wirkungseinheiten) überschreitet. Berechne den gesamten Wirkungsfaktor bis zum völligen Abklingen der Krankheit, wenn das Medikament nach 3 Tagen eingenommen wird.
Wir berchnen beide Teilintegrale einzeln:
≈