Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Randfunktion zur Integralfunktion

Allgemeine Info

Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du selbständig die Aufgaben bearbeiten. Du benötigst Papier und Stifte, Lineal und Taschenrechner. Zu jedem Kapitel wurden Aufgaben beigefügt, die Dir dabei helfen das Wissen besser zu verstehen und zu vertiefen. Bei diesen Aufgaben handelt es sich um 3 verschiedene Schwierigkeitsstufen, die farblich gekennzeichnet sind:

• Aufgaben mit gelbem Titel sind zum Wiederholen und Vertiefen
• Aufgaben mit blauem Titel sind von mittlerer Schwierigkeit
• Aufgaben mit grünem Titel sind Knobelaufgaben

Die mit einem Sternchen markierten Aufgaben sind insbesondere für den LK gedacht.

Viel Erfolg bei der Bearbeitung dieses Lernpfades!

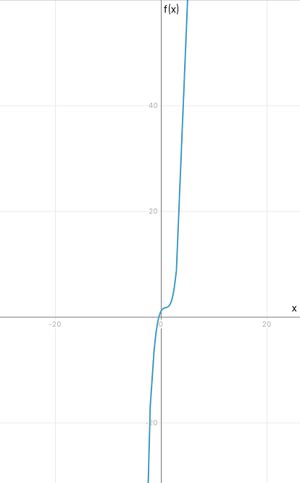
Einführung: Integral

Was ist ein Integral?

Die Fläche unter einem Graphen kann durch den gemeinsamen Grenzwert von Ober- und Untersummenfolgen bestimmt werden. Dies nennt man das Integral von $f$ über das Intervall $[a, b]$ und schreibt dafür $\int_{a}^{b} f(x) dx$.

Die Funktion $f$ heißt dann über $[a, b]$ integrierbar. Dabei ist $a$ die untere und $b$ die obere Integrationsgrenze und $f$ die Rand- oder auch Integrandfunktion.

Betrachtet man die Werte von Integralen in Abhängigkeit von einer festen unteren Grenze $a$ und einer variablen (anstelle einer festen) oberen Grenze $x$ und verwendet deshalb $t$ als Variable der Integrandfunktion $f$, so erhält man eine Integralfunktion $F_a(x) = \int_{a}^{x} f(t) dt, x\in [a, b].$

$F_a$ ist also eine Funktion, die jedem $x \in [a, b]$ das Integral von $f$ über $[a; x]$ zuordnet. $x$ ist dabei die Funktionsvariable, in die eingesetzt werden darf, während $t$ eine gebundene Variable ist, in die nicht eingesetzt werden darf.

Eine Funktion $F$ heißt Stammfunktion zur Funktion $f$, wenn gilt $F'(x) = f(x)$ für alle $x \in (a, b)$.

Rechnen mit Integralen

Aufgabe 1: Rechenregeln

Welche der folgenden Rechenregeln sind richtig und welche falsch?

1 $\int_{a}^{c} f(x) dx = \int_{a}^{b} f(x) dx - \int_{b}^{c} f(x) dx$

	Wahr
	Falsch

2 $\int_{a}^{c} f(x) dx = \int_{a}^{b} f(x) dx + \int_{b}^{c} f(x) dx$

	Wahr
	Falsch

3 $\int_{a}^{c} f(x) dx = \int_{a}^{b} f(x) dx + \int_{a}^{c} f(x) dx$

	Wahr
	Falsch

1 $\int_{a}^{b} c\cdot f(x) dx = c\cdot \int_{a}^{b} f(x) dx$

	Wahr
	Falsch

2 $\int_{a}^{b} c\cdot f(x) dx = c^2\cdot \int_{a}^{b} f(x) dx$

	Wahr
	Falsch

3 $\int_{a}^{b} c\cdot f(x) dx = c + \int_{a}^{b} f(x) dx$

	Wahr
	Falsch

1 $\int_{a}^{b} ( f(x) + g(x) ) dx = \int_{a}^{\frac{b}{2}} f(x) dx + \int_{a}^{\frac{b}{2}} g(x) dx$

	Wahr
	Falsch

2 $\int_{a}^{b} ( f(x) + g(x) ) dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx$

	Wahr
	Falsch

3 $\int_{a}^{b} ( f(x) + g(x) ) dx = \int_{a}^{b} f(x) dx + \int_{b}^{a} g(x) dx$

	Wahr
	Falsch

1 $\int_{a}^{b} ( f(x) - g(x) ) dx = \int_{a}^{\frac{b}{2}} f(x) dx - \int_{a}^{\frac{b}{2}} g(x) dx$

	Wahr
	Falsch

2 $\int_{a}^{b} ( f(x) - g(x) ) dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx$

	Wahr
	Falsch

3 $\int_{a}^{b} ( f(x) - g(x) ) dx = \int_{a}^{b} f(x) dx - \int_{a}^{b} g(x) dx$

	Wahr
	Falsch

1 $\int_{a}^{b} f(x) dx = -\int_{a}^{b} f(x) dx$

	Wahr
	Falsch

2 $\int_{a}^{b} f(x) dx = \int_{a}^{b} \frac{1}{f(x)} dx$

	Wahr
	Falsch

3 $\int_{a}^{b} f(x) dx = -\int_{b}^{a} f(x) dx$

	Wahr
	Falsch

1 $\int_{a}^{b} f(x) dx$ ≤ $\int_{a}^{b} g(x) dx$, wenn $f(x)$ ≤ $g(x)$ für alle $x\in [a; b]$

	Wahr
	Falsch

2 $\int_{a}^{b} f(x) dx$ ≥ $\int_{a}^{b} g(x) dx$, wenn $f(x)$ ≤ $g(x)$ für alle $x\in [a; b]$

	Wahr
	Falsch

3 $\int_{a}^{b} f(x) dx$ ≤ $\int_{a}^{b} g(x) dx$, wenn $f(x)$ ≥ $g(x)$ für alle $x\in [a; b]$

	Wahr
	Falsch

1 $|\int_{a}^{b} f(x) dx| = \int_{a}^{b} f(x) dx$

	Wahr
	Falsch

2 $|\int_{a}^{b} f(x) dx|$ ≥ $\int_{a}^{b} |f(x)| dx$

	Wahr
	Falsch

3 $|\int_{a}^{b} f(x) dx|$ ≤ $\int_{a}^{b} |f(x)| dx$

	Wahr
	Falsch

1 $\int_{a}^{a} f(x) dx = 1$

	Wahr
	Falsch

2 $\int_{a}^{a} f(x) dx = 0$

	Wahr
	Falsch

3 $\int_{a}^{a} f(x) dx = \sqrt{f(x)}$

	Wahr
	Falsch

Der Hauptsatz der Differential- und Integralrechnung

Die Verbindung zwischen Integralen und Differentialen

Der Hauptsatz beschreibt, wie sich Ableitung und Integration umkehren lassen. Durch ihn lassen sich beispielsweise Integrale leichter ausrechnen. Der Hauptsatz besteht aus zwei Teilen, die es zu unterscheiden gilt.

Der erste Teil des Hauptsatzes

Wenn f eine stetige Funktion auf dem Intervall $[a; b]$ ist, so gilt für jede Stammfunktion F auf dem Intervall $[a; b]$ die Formel: $\int_{a}^{b} f(x)\, dx = F(b) - F(a)$, wobei $F'(x) = f(x)$ ist. Mit dieser Variante lässt sich auch die Stammfunktion F (re-)konstruieren, wenn du deren Ableitung und einen Anfangswert a kennst. Dies kannst du mit dieser Formel machen: $F(x) = F(a) + F(x) - F(a) = F(a) + \int_{a}^{x} f(t)\, dt$

Gegeben ist die Funktion $f(x) = x^3 - 6 \cdot x + 11\frac{3}{4} \cdot x - 5\frac{1}{2}$ auf dem Intervall $[1; 3]$

1 Schritt: Ermittle das unbestimmte Integral, also die Stammfunktion F: $F(x) = \int x^3 - 6x^2 +11\frac{3}{4}x - 5\frac{1}{2} = \frac{1}{4}x^4 - 2x^3 + 5\frac{7}{8}x^2 - 5\frac{1}{2}x + C$

2 Schritt: Berechne F(a) und F(b) durch Einsetzen der unteren bzw. oberen Intervallgrenzen in F(x): $F(1) = \frac{1}{4} \cdot 1^4 - 2 \cdot 1^3 + 5\frac{7}{8} \cdot 1^2 - 5\frac{1}{2} \cdot 1 + C = - 1\frac{3}{8} + C$ $F(3) = 2\frac{5}{8} + C$

3 Schritt: Bilde die Differenz $F(b-F(a)$:

$F(3) - F(1) = 2 \frac{5}{8} + C - (- 1\frac{3}{8} + C) = 4$

Der zweite Teil des Hauptsatzes

Die zweite Variante des Hauptsatzes ist sozusagen die Umkehrung der ersten Variante. Nun gehen wir vom Integral, also der Stammfunktion $F$ aus und bestimmen $f(x)$ . Hierbei gilt:

$f(x) = F'(x) = F'(F(a) + \int_{a}^{x} f(t)\, dt = F'(a) + F'(\int_{a}^{x} f(t)\, dt) = F'(\int_{a}^{x} f(t)\, dt) = F'( F(x) - F(a))$

Mittelwerte mithilfe des Integrals bestimmen

Mittelwert

Der Mittelwert einer Funktion lässt sich über das Integral bestimmen. Bezeichnen wir mit $f$ eine Funktion. Der Mittelwert einer Funktion $f$ lässt sich auf dem Intervall $[a, b]$ berechnen. Hierzu benötigst du folgende Formel: $M= \frac{1}{b-a} \cdot \int_{a}^{b} f(x)\,dx$

Ein Auto beschleunigt 40 Sekunden lang. Die Geschwindigkeit zum Zeitpunkt $t$ ist gegeben durch $f(t)= \frac{5}{4} \cdot t$, wobei $t$ in Sekunden und die Funktion $f(t)$ in $m/s$ angegeben wird. Wie groß ist die Durchschnittsgeschwindigkeit?

Vorgehen zur Bearbeitung der Beispielaufgabe

1. Benutzung der Formel: $M= \frac{1}{b-a} \cdot \int_{a}^{b} f(x)\,dx$
2. Einsetzen der Gegebenheiten in die Formel: $M= \frac{1}{40-0} \cdot \int_{40}^{0} \frac{5}{4} \cdot t \,dt$
3. Ausrechnen: $M= \frac{1}{40-0} \cdot \int_{40}^{0} \frac{5}{4} \cdot t \,dt= \frac{1}{30} \cdot [\frac{5}{8} \cdot t^2]_{40}^{0}=\frac{1}{40} \cdot \frac{1}{40} \cdot 40^2 = 25$
4. Antwortsatz formulieren: Die Durchschnittsgeschwindigkeit betrug beim Auto $25 m/s$.

Aufgabe 2: Der Goldpreis

Hierfür benötigst du einen Zettel und einen Stift.

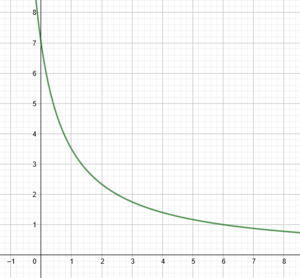
Der Goldpreis wird innerhalb von 4 Tagen durch die Funktion $f(x)= 2 \cdot x^3 - 12 \cdot x^2 + 20 \cdot x + 30$ dargestellt, $x$ in Tagen,$f(x)$ in $\frac{Euro}{g}$ . Berechne den Durchschnittspreis in den ersten 4 Tagen.

Benutze die Formel und setze alles ein was du hast

$= 38$

$M = \frac{3}{4} \cdot \int_{4}^{0} 2 \cdot x^3 - 12 \cdot x^2 + 20 \cdot x + 30 \, dx = \frac{1}{4} \cdot (\frac{4^4}{2} - 4 \cdot 4^3 + 10 \cdot 4^2 + 30 \cdot 4) = 38$

Aufgabe 3: Bakterien

Hierfür benötigst du einen Zettel und einen Stift.

In einem Labor werden Bakterien gezüchtet. Die Anzahl der Bakterien innerhalb von 10 Tagen ist durch die Funktion $f(x) = - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1$ gegeben , wobei $x$in Tagen mit $0 \leq\ x \leq 10$.

a) Wie viele Bakterien gibt es am 8. Tag?

Setze für $x = 8$ ein

$f(8) = 358$

b) Wie viele Bakterien gibt es in den ersten 8 Tagen im Durchschnitt?

Nutze die Formel des Mittelwerts

$= 1635 \frac{13}{100}$

$M = \frac{1}{8 - 0} \cdot \int_{8}^{0} - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1 \,dx = \frac{1}{8} \cdot ( - \frac{1}{5} \cdot 8^5 + 10 \cdot 8^4 - \frac{500}{3} \cdot 8^3 + 1000 \cdot 8^2 + 8 - 0) = 1635 \frac{13}{100}$

c) Wie viele Bakterien werden durchschnittlich zwischen dem 2. und 4. Tag gezüchtet?

Nutze die Formel des Mittelwerts. Bedenke dass du nun ein anderes Intervall als bei b) hast.

$= 2435 \frac{2}{15}$

$M = \frac{1}{4 - 2} \int_{4}^{2} - x^4 + 40 \cdot x^3 - 500 \cdot x^2 + 2000 \cdot x + 1 \,dx = \frac{1}{2} \cdot ( - \frac{1}{5} \cdot 4^5 + 10 \cdot 4^4 - \frac{500}{3} \cdot 4^3 + 1000 \cdot 4^2 + 4 - ( - \frac{1}{5} \cdot 2^5 + 10 \cdot 2^4 - \frac{500}{3} \cdot 2^3 + 1000 \cdot 2^2 + 2 )) = 2435 \frac{2}{15}$

Aufgabe 4: Integrieren mit dem Hauptsatz der Differential- und Integralrechnung

Hierfür benötigst du einen Zettel und einen Stift, um die Aufgabe zu bearbeiten.

Die Abbildung zeigt das Schaubild der Funktion $f$ mit $f(x) = \frac{3}{4}x^3 - 2x^2 + 2x + 1$

Abbildung der Funktion f(x)

a) Welchen Wert erhältst du für das Integral im Intervall $[-1; 3]$?

Berechne zunächst die Stammfunktion

$= 3\frac{1}{3}$

$\int_{3}^{-1} \frac{3}{4}x^3 - 2x^2 + 2x + 1 \,dx = 4\frac{1}{8} - \frac{19}{24} = 3\frac{1}{3}$

b) Wie lautet der Mittelwert?

Nutze das Intervall von Aufgabe a)

$= \frac{25}{12}$

$M =\frac{1}{3 + 1}\int_{3}^{-1} \frac{3}{4}x^3 - 2x^2 + 2x + 1 \,dx = \frac{1}{4} (\frac{147}{16}- \frac{41}{48}) = \frac{25}{12}$

Aufgabe 5: Das Kirchenfenster

Hierfür benötigst du einen Zettel und einen Stift, um die Aufgabe zu bearbeiten.

Ein Kirchenfenster wird oben durch die Funktion $f(x) = - x^2 + 10 \cdot x - 17$ im Intervall $[3; 7]$ begrenzt, $x$ und $f(x)$ in Metern. Wie viel $m^2$ Glas wurde benötigt?

Mache dir eine Skizze

$= \frac{80}{3}$

$\int_{7}^{3} - x^2 + 10 \cdot x - 17 \,dx = ( - \frac{7^3}{3} + 5 \cdot 7^2 - 17 \cdot 7) - ( - \frac{3^3}{3} + 5 \cdot 3^2 - 17 \cdot 3) = \frac{80}{3}$

Partielle Integration

Partielle Integration

Die partielle Integration ist eine Methode, die die Integration von Produkten zweier Funktionen ermöglicht. Sie beruht auf der Produktregel und wird daher auch Produktintegration genannt. Dabei ist es von Vorteil, wenn die eine Funktion leicht abzuleiten und die andere leicht zu integrieren ist.

Allgemein definiert man die Formel der partiellen Integration so:$\int f'(x) \cdot g(x)\,dx = [f(x) \cdot g(x)] - \int f(x) \cdot g'(x)\,dx$

Dabei ist $\int f'(x) \cdot g(x)\,dx$ das ursprüngliche Integral.

$f'(x)$ ist die leicht zu integrierende Funktion.

$g(x)$ ist die leicht abzuleitende Funktion.

Die Beispielfunktion lautet: $h(x) =cos(x) \cdot x$

$cos(x)$ lässt sich leicht integrieren. Also $f(x)=cos(x)$ und $f'(x)=sin(x)$

$x$ lässt sich leicht ableiten. Also $g(x)=x$ und $g'(x)=1$

Nun müssen unsere Funktionen und deren Ableitungen in die oben genannte Formel eingesetzt werden: $\int f'(x) \cdot g(x)\,dx = [f(x) \cdot g(x)] - \int f(x) \cdot g'(x)\,dx$ $\int cos(x) \cdot x\,dx = [sin(x) \cdot x] - \int sin(x) \cdot 1\,dx = [sin(x) \cdot x] - [-(cos(x))] = sin(x) \cdot x + cos(x)$

Die integrierte Funktion bzw. Stammfunktion von $h(x) = cos(x) \cdot x$ lautet somit:$H(x) = sin(x) \cdot x + cos(x)+C$

Integration durch Substitution

Integration durch Substitution

Die Integration durch Substitution ist eine weitere Methode der Integration, welche auf der Kettenregel beruht. Dabei muss eine Verknüpfung zweier Funktionen innerhalb dieses Integrals vorhanden sein. Allgemein wird ihre Formel folgendermaßen definiert:$\int_a^b f(g(x)) \cdot g'(x)\, dx = \int_{g(a)}^{g(b)} f(z)\, dz$

Vorgehen:

1. Zunächst wird die innere Funktion $g(x)$ dieser verknüpften Funktion durch eine Variable $z$ ersetzt. Also $z = g(x)$
2. Die Gleichung wird nach $x$ abgeleitet. Also $z = g(x) \Longrightarrow dz = g'(x) dx$
3. und dann nach $dx$ umgeformt: $dz = g'(x) dx \Longrightarrow dx = \frac{dz}{g'(x)}$
4. Falls im Integral die Grenzen $a$ und $b$ angegeben wurden, müssen diese durch Einsetzen in die Gleichung $g(x)$ angepasst werden: $a \longrightarrow g(a)$ neue untere Grenze $b \longrightarrow g(b)$ neue obere Grenze
5. Die nach $dx$ umgeformte Gleichung und die neuen Grenzen werden nun in das Integral eingesetzt.
6. Nun folgt das normale Integrationsverfahren. Also: $\int_{g(a)}^{g(b)} f(z)\, dx = \left[F(z)\right]^{g(b)}_{g(a)}$
7. Die Resubstitution ist nun der letzte Schritt, in dem das Ersetzen der inneren Funktion $g(x)$ durch die Variable $z$ wieder rückgängig gemacht wird. Das heißt: $\left[F(z)\right]^{g(b)}_{g(a)} = \left[F(g(x))\right]^{b}_{a}$

Die zu integrierende Funktion lautet: $h(x)=sin(2x)$

Zu bestimmen: $H(x) = \int_0^{\frac{1}{2} \pi} sin(2x)\, dx$. Dabei sind die Grenzen $a=0$ und $b= \frac{1}{2} \pi$

1. Die innere Funktion ist $g(x) = 2x = z$.
2. Ableitung der Funktion: $g'(x)=2 \cdot dx=dz$.
3. Umformen nach $dx$: $2 \cdot dx= dz \Longrightarrow dx = \frac{dz}{2}$.
4. Die allgemeine Integration lautet nun: $\frac{1}{2} \cdot \int_{g(a)}^{g(b)} sin(z)\, dz = \frac{1}{2} \left[-cos(z)\right]^{g(b)}_{g(a)}$.
5. Anpassung der alten Grenzen $a \longrightarrow g(a)$ bzw. $b \longrightarrow g(b)$. Das heißt für unsere untere Grenze $a=0$ gilt $g(0)=2 \cdot 0 = 0$ und für die obere Grenze $b=\frac{1}{2} \pi$ gilt $g(\pi)= 2 \cdot \frac{1}{2} \pi = \pi$.
6. Einsetzen in das Integral: $\int_{g(a)}^{g(b)} sin(z)\, \frac{dz}{2} = \frac{1}{2} \int_{0}^{\pi} sin(z)\, dz$.
7. Die Funktion $g(x)$ wird nun für die Variable $z$ ersetzt: $\frac{1}{2} \cdot \int_{0}^{\pi} sin(z)\, dz = \frac{1}{2} \left[-cos(2x)\right]^{\pi}_{0}.$
8. Für die speziellen Grenzen berechnen wir nun die Fläche: $\frac{1}{2} \left[-cos(z)\right]^{\pi}_{0} = \frac{1}{2} (-cos(\pi)-(-cos(0)) = \frac{1}{2} (1+1) = 1$

Die integrierte Funktion bzw. Stammfunktion von $h(x)= sin(2x)$ lautet: $H(x) = - \frac{1}{2} cos(2x)+C$

Aufgaben zu den verschiedenen Integrationsverfahren

Aufgabe 6: Integration von komplexeren Funktionen

Wie lautet die Stammfunktion dieser Funktionen? Hierfür benötigt ihr einen Zettel und einen Stift, um die Funktion schriftlich zu integrieren.

a) $f(x) = x \cdot sin(x)$

Welche der drei eingeführten Integrationsverfahren passt den am besten zu einem Produkt von zwei Funktionen?

Wenn du die partielle Integration verwendest, setze die leicht abzuleitende Funktion $g(x)=x$ und die leicht zu integrierende Funktion $f'(x)=sin(x)$.

$F(x)= \int_a^b x \cdot sin(x) \,dx = \left[x \cdot (-cos(x)) \right] - \int_a^b 1 \cdot (-cos(x)) \, dx = x \cdot (-cos(x)) - (-sin(x)) = - x \cdot cos(x) + sin(x) + C$

b) $f(x)= (x + 2)^2$ im Intervall $[1; 6]$

Nutze den Hauptsatz der Differential- und Integralrechnung

Bilde die Stammfunktion von f(x), betrachte die Grenzen zunächst einzeln und denke an die binomischen Formeln

$= \frac{485}{3}$

$F(x)= \frac{x^3}{3} + 2 \cdot x^2 + 4 \cdot x$ daraus folgt $F(6) - F(1) = (\frac{6^3}{3} + 2 \cdot 6^2 + 4 \cdot 6) - (\frac{1^3}{3} + 2 \cdot 1^2 + 4 \cdot 1) = \frac{216}{3} - \frac{19}{3} = \frac{485}{3}$

c) $j(x)= \frac{cos(4x+1)}{2}$

An welche Integrationsmethode erinnert dich diese verketteten Funktionen?

Hast du die Integration durch Substitution erkannt? Dann setze die innerer Funktion $g(x)=4x+1 = z$ und leite sie nach $x$ ab.

$J(x)= \int \frac{cos(z)}{2}\, \frac{dz}{4} = \int \frac{cos(z)}{8}\, dz = \frac{1}{8} \int cos(z)\, dz$. Wenn du jetzt so weit gekommen bist, was fehlt dann nur noch?

Die integrierte Funktion lautet: $J(x)= \frac{1}{8} \int cos(z)\, dz = \frac{1}{8} \left[ sin(z) \right] = \frac{sin(4x+1)}{8} + C$.

d) $k(x)= cos(x) \cdot sin(x)$

Auf den ersten Blick wirkt zwar die Integralmethode "partielle Integration" passend, aber welche Methode würde vielleicht eher zum Ziel führen?

Was passiert, wenn du die abgeleitete, nach $dx$ umgeformte Funktion $g(x)= sin(x) = z$ in das Integral für $dx$ einsetzt?

Wenn du erkannt hast, dass du $sin(x)$ kürzen kannst, erhälst du das Integral $\int z\, dz$. Den kannst du jetzt ganz leicht integrieren.

Die integrierte Funktion lautet: $K(x)=  \int z\, dz = \left[\frac{1}{2} \cdot z^2 \right] = \frac{(sin)^2(x)}{2} + C$.

e) $f(x)= (4 - x)$ im Intervall $[1; 4]$

Nutze den Hauptsatz der Differential- und Integralrechnung

Bilde die Stammfunktion von f(x) und betrachte die Grenzen zunächst einzeln

$= \frac{9}{2}$

$F(x)= 4 \cdot x - \frac{x^2}{2}$ daraus folgt $F(4) - F(1) = (4 \cdot 4 - \frac{4^2}{2} ) - (4 \cdot 1 - \frac{1^2}{2}) = 8 - \frac{7}{2} = \frac{9}{2}$

Aufgabe 7: Stammfunktionen zuordnen

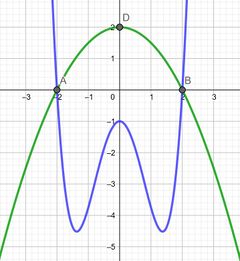
Ordne die Funktionen ihren passenden Stammfunktionen zu!

Flächeninhalte von Integralen

Aufgabe 8: Flächeninhalte berechnen

Berechne den Flächeninhalt der folgenden Integrale! Dafür wirst du für ein paar Aufgaben einen Zettel und einen Stift benötigen.

Aufgabe 9: Zahnlogo

Skizze des Zahn-Logos

In einer Zahnarztpraxis soll ein neues Logo entworfen werden. Dazu wurde die nebenstehende Zeichnung angefertigt, welche durch die Funktionen $f(x)=- \frac{x^2}{2} + 2$ und $g(x)= x^4- \frac{15}{4} \cdot x^2 - 1$ das Zahnlogo bildet. Dabei entspricht eine Längeneinheit in dem Graphen $1 cm$. Nun soll dieses Logo mit einer Dicke von $1 mm$ aus Silber ($1 cm^2$ Silber wiegt $10,5 g$) produziert werden. Wie schwer wird das Logo dann werden?

Bearbeite diese Textaufgabe am besten schriftlich auf einem Zettel.

Zuerst soll die Fläche des Logos berechnet werden. Welche Grenzen gelten dabei für das Integral?

Zur Berechnung der Fläche wird dieses Integral genötigt: $\int_{-2}^2 f(x) + g(x)\, dx$.

Hast du daran gedacht, alle Einheiten einheitlich anzupassen? Die Dicke von $1 mm$ muss auf jeden Fall noch in $cm$ umgerechnet werden.

Wenn du die Fläche des Logos $A_{Logo}$ wie in Tipp 1 berechnet hast, kannst du das $V_{Logo}$ nun durch das Produkt von $A_{Logo}$ und der Dicke (beachte Tipp 2!) berechnen.

Zunächst wird der Flächeninhalt berechnet:

$A_{Logo} = \int_{-2}^2 f(x) + g(x)\, dx = \int_{-2}^2 (- \frac{x^2}{2} + 2) + (x^4- \frac{15}{4} \cdot x^2 - 1 )\, dx = \int_{-2}^2 x^4- \frac{15}{4} \cdot x^2 - \frac{1}{2} \cdot x + 1 \, dx = \left[ \frac{1}{5} x^5 - \frac{5}{4} x^3 - \frac{1}{4} x^2 + x \right] = 3,2 cm^2$

Wenn ihr die Fläche des Logos berechnet habt, könnt ihr mit Hilfe der angegebenen Dicke des Logos das Volumen berechnen:

$V_{Logo}= A_{Logo} \cdot Dicke_{Logo} = 3,2 {cm}^2 \cdot 0,1 cm = 0,32 {cm}^3$

Das Gewicht wird dann wie folgt angegeben:$V_{Logo} \cdot Gewicht_{Silber}= 0,32 [{cm}^3] \cdot 10,5 [g] = 3,36 [g]$ Das fertige Logo aus Silber wiegt $3,36 g$.

Rotationskörper (Zusatz: nur für LK's)

⭐ Rotationskörper und Raumintegrale

Lässt man den Graphen einer Funktion um die x-Achse rotieren, so entsteht ein sogenannter Rotationskörper. Für seinen Rauminhalt gilt $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$.

Als Beispiel betrachten wird das Volumen einer Kugel mit Radius $r$, die durch die Rotation des Graphen der Funktion $f$ mit $f(x) = \sqrt{r^2-x^2}$ im Intervall $[-r; r]$ um die $x$-Achse entsteht. Mit der Formel für den Rotationskörper erhält man nun das Volumen der Kugel: $V = \pi\int_{-r}^{r}(r^2-x^2) dx = \left[\pi(r^2\cdot x - \frac{1}{3}x^3)\right]_{-r}^{r} = \frac{4}{3}\pi\cdot r^3$.

Hier ein weiteres Beispiel einer Sinus-Funktion, das veranschaulicht, wie du dir Rotationskörper vorstellen kannst.

⭐ Aufgabe 10: Rotationskörper und Raumintegrale

Funktionsgraph von $f(x)$

Bearbeite diese Aufgabe am besten schriftlich auf einem Zettel.

Gegeben sei die Funktion $f$ mit $f(x) = \frac{7}{1+x}, x \in\mathbb{R}_+$. Die Fläche von $f$ rotiere um die $x$-Achse.

Berechne den Inhalt des entstehenden Drehkörpers:

a) im Intervall $[0; a]$

Nutze die Formel zur Inhaltsberechnung von Rotationskörpern $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$ und setze die Funktion $f(x)$ sowie die Grenzen $0$ und $a$ ein.

$V_{rot}= \pi \int_{a}^{b} ( f(x) )^2 dx = \pi \int_{0}^{a} ( \frac{7}{1+x} )^2 dx = \pi \int_{0}^{a} \frac{49}{(1+x)^2} dx = 49\pi \int_{0}^{a} (1+x)^{-2} dx = 49\pi \left[ -(1+x)^{-1} \right]_{0}^{a} = -\frac{49\pi}{1+a} + \frac{49\pi}{1} = 49\pi - \frac{49\pi}{1+a}$

b) im Intervall $[0; 6]$

Nutze die Formel zur Inhaltsberechnung von Rotationskörpern $V_{rot} = \pi \int_{a}^{b} ( f(x) )^2 dx$ und setze die Funktion $f(x)$ sowie die Grenzen $0$ und $6$ ein.

$V_{rot}= \pi \int_{a}^{b} ( f(x) )^2 dx = \pi \int_{0}^{a} ( \frac{7}{1+x} )^2 dx = \pi \int_{0}^{a} \frac{49}{(1+x)^2} dx = 49\pi \int_{0}^{a} (1+x)^{-2} dx = 49\pi \left[ -(1+x)^{-1} \right]_{0}^{a} = -\frac{49\pi}{1+a} + \frac{49\pi}{1} = 49\pi - \frac{49\pi}{1+a} = 49\pi - 7\pi = 42\pi$.

⭐ Aufgabe 11: Rotationskörper und Raumintegrale

Funktionsgraphen von $g(x)$ (orange) und $h(x)$ (lila)

Sei eine Funktion $g$ gegeben mit $g(x) = \frac{1}{6} x^2 + 1, x\in\mathbb{R}$ sowie die Funktion $h$ mit $h(x) = -\frac{1}{3} x + 5, x\in\mathbb{R}$.

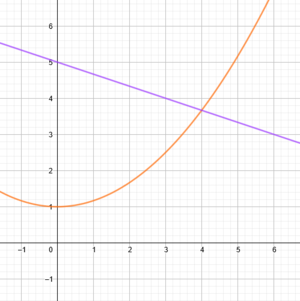
Die Graphen von $g$ und $h$ begrenzen mit der $y$-Achse eine Fläche.

Berechne den Inhalt des Körpers, der entsteht, wenn diese Fläche um die $x$-Achse rotiert.

Bearbeite diese Aufgabe am besten schriftlich auf einem Zettel.

Überlege dir, wie die Formel aussieht, die du zur Berechnung des Inhalts zwischen zwei Funktionen nutzen kannst. Überlege dir außerdem, in welchem Intervall das Integral berechnet werden soll.

Die Formel zur Inhaltsberechnung lautet: $V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx$, wobei $b$ die Schnittstelle von $h(x)$ und $g(x)$ ist. Berechne also zunächst die Schnittstelle.

Die Schnittstelle von $h(x)$ und $g(x)$ ist $4$. Setze dies nun als obere Grenze in deine Formel (siehe Tipp 2) ein und berechne die Integrale. Nutze dafür die Substitution sowie dein Wissen über Potenzregeln und Linearität.

1. Schnittstelle berechnen:

$g(x) = h(x) \Leftrightarrow \frac{1}{6} x^2 + 1 = -\frac{1}{3} x + 5 \Leftrightarrow \frac{1}{6} x^2 + \frac{1}{3} x - 4 = 0 \Leftrightarrow x^2 + 2x - 24 = 0 \Leftrightarrow x_{1,2} = -1 \pm \sqrt{1^2+24} = -1 \pm 5 \Rightarrow x_1 = 4, x_2 = -6$ Für uns interessant ist nur der Wert im positiven $x$-Bereich, da die Fläche links von der $y$-Achse laut Aufgabenstellung nicht betrachtet wird.

2. Integrale berechnen:

$V_{rot} = \pi \int_{0}^{b} ( h(x) )^2 dx - \pi \int_{0}^{b} ( g(x) )^2 dx = V_{rot} = \pi \int_{0}^{4} ( -\frac{1}{3} x + 5 )^2 dx - \pi \int_{0}^{4} ( \frac{1}{6} x^2 + 1 )^2 dx = \pi \int_{0}^{4} ( 5 -\frac{x}{3} )^2 dx - \pi \int_{0}^{4} ( \frac{x^4}{36} + \frac{x^2}{3} + 1 ) dx$

$\rightarrow$ Substituiere $u = 5 - \frac{x}{3} \Rightarrow \frac{du}{dx} = -\frac{1}{3} \rightarrow -3\pi\int u^2 du$

Nun wird die Potenzregel angewendet und resubstitutiert. Im zweiten Term kann zudem die Linearität des Integrals ausgenutzt werden. Insgesamt gilt dann:

$V_{rot} = \pi \left[ \frac{(x-15)^3}{27} \right]_{0}^{4} - \pi \left[ \frac{x^5+20x^3}{180}+x \right]_{0}^{4} \approx 185,05.$