Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der Änderungsrate zum Änderungseffekt
In diesem Kapitel kannst du die Idee und die Anwendung des Integrals wiederholen und durch gezielte Aufgaben üben und verbessern. Die Grundlage hierfür ist, dass du die Eigenschaften von Funktionen erkennst und untersuchen sowie ableiten kannst.
Du sollst hier für dich verinnerlichen, was überhaupt hinter dem Begriff des Integrals steckt und kannst darüber hinaus Grundlagen für die Anwendung mit Integralen wiederholen aber auch vertiefen.
Zum Einstieg findest du eine Herleitung des Integrals aus dem Kontext der Differentialrechnung. Dabei werden dir die zwei Oberbegriffe des Kapitels Änderungsrate und Änderungseffekt erläutert. Anschließend folgen einige Aufgaben zum Integral bei denen es besonders auf den Zusammenhang von Differential- und Integralrechnung ankommt. Die Aufgaben werden in drei unterschiedliche Schwierigkeitsstufen eingeteilt so dass du jederzeit die Möglichkeit hast auf deinem Leistungsstand zu arbeiten.
In Aufgaben, die orange gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.
Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit. Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.Inhaltsverzeichnis
Herleitung des Integrals
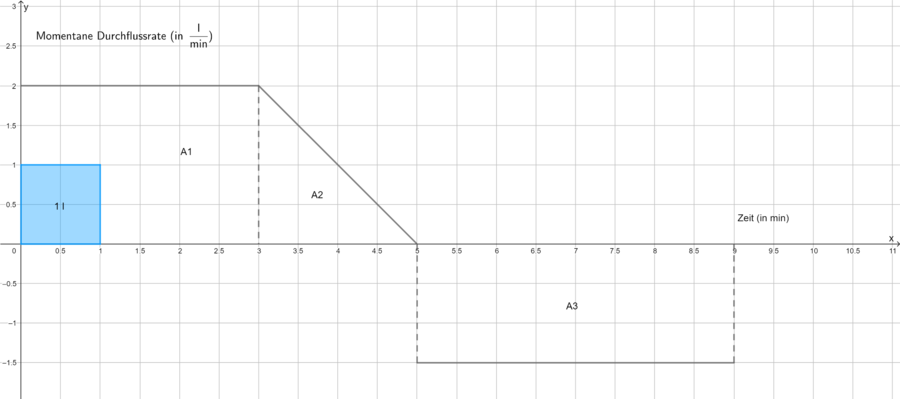
Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur ist die momentane Durchflussrate f der Leitung für das Intervall dargestellt.
Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank?
Im Intervall beträgt der Zufluss
. In diesen 3 Minuten fließen
in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall
beträgt die mittlere Zuflussrate
. In diesen 2 Minuten kommen
dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall
ist die Durchflussrate negativ. Es fließen
ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall
mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser orientierte Flächeninhalt beträgt beim Wassertank:
Die Funktion sei auf dem Intervall
stetig und
sei eine beliebige Rechtecksumme zu
über dem Intervall
.
Dann heißt der Grenzwert Integral der Funktion
zwischen den Grenzen
und
.
Man schreibt dafür:
Die Funktion sei stetig auf dem Intervall
. Dann gilt:
Rechenregeln und Stammfunktionen bilden
Eine Funktion heißt Stammfunktion zu einer Funktion
auf einem Intervall
, wenn für alle
in
gilt:
.
Sind
und
Stammfunktionen von
auf einem Intervall
, dann gibt es eine Konstante
, sodass für alle
in
gilt:
Zur Funktion mit
ist
mit
eine Stammfunktion.
Zur Funktion
mit
ist
mit
eine Stammfunktion.
Sind
und
Stammfunktionen von
und
, so gilt für die zusammengesetzten Funktionen:
Gelerntes Wiederholen und Vertiefen
Du erkennst, dass der orientierte Flächeninhalt nicht mit dem Wert des Flächeninhalt zwischen Graph und x-Achse übereinstimmt. Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten.
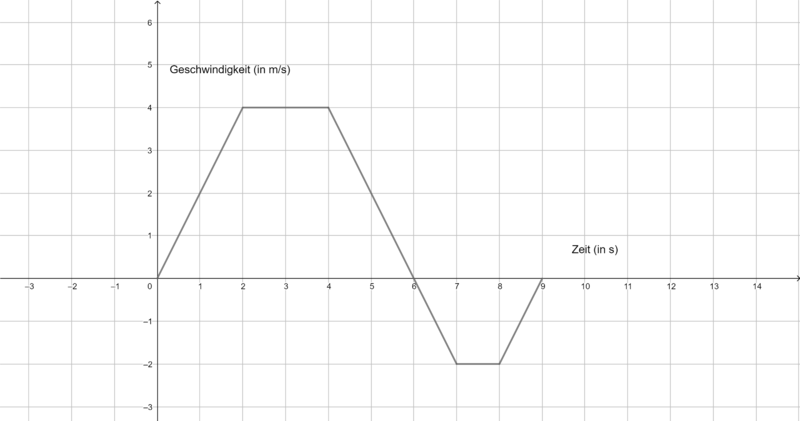
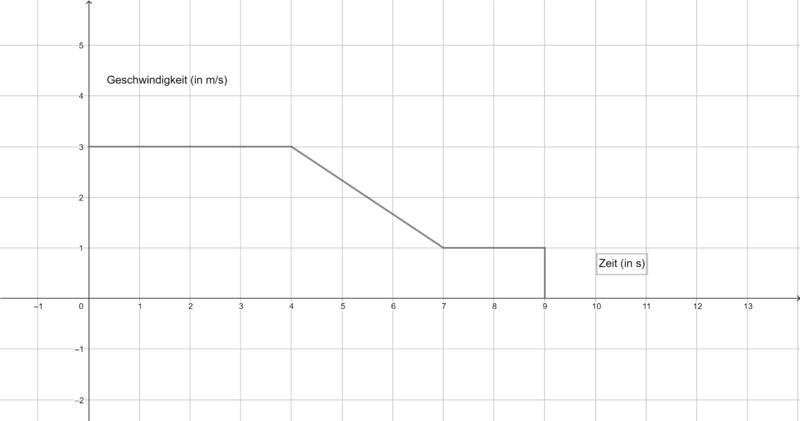
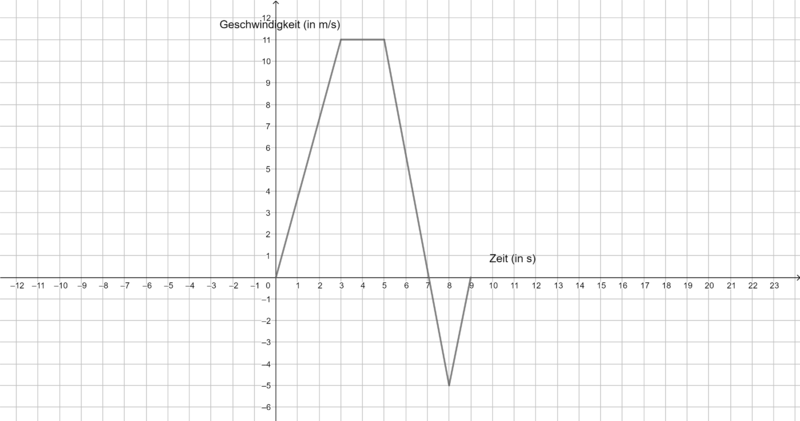
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die vom Startpunkt zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren.
a)Fläche oberhalb der x-Achse:
Flächer unterhalb der x-Achse:
Integral/orientierter Flächeninhalt:
Der Körper hat eine Strecke von 12 m vom Startpunkt zurückgelegt.
Fläche oberhalb der x-Achse:
Flächer unterhalb der x-Achse:
Integral/orientierter Flächeninhalt:
Der Körper hat eine Strecke von 20 m vom Startpunkt zurückgelegt.
Fläche oberhalb der x-Achse:
Flächer unterhalb der x-Achse:
Integral/orientierter Flächeninhalt:
Der Körper hat eine Strecke von 44,5 m vom Startpunkt zurückgelegt.
Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden.

Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten
Aufgaben mittlerer Schwierigkeit
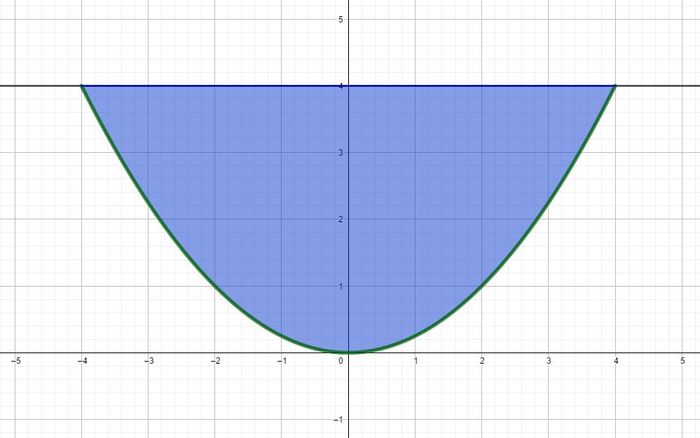
Der Boden eines 2km langen Kanals hat die Form einer Parabel (siehe Abbildung). Dabei entspricht eine Längeneinheit 1m in der Wirklichkeit.
- a) Erstelle eine Funktion f, die den Verlauf des Kanalgrundes angibt.
- b) Berechne den Inhalt der Querschnittsfläche A des Kanals [in
]. Nimm dabei an, dass die Funktion f mit
den Grundverlauf des Kanals darstellt.
- c) Wie viel Wasser [in m^3] befindet sich im Kanal, wenn er komplett gefüllt ist?
- d) Schwer: Wie viel Prozent der maximalen Wassermenge befindet sich im Kanal, wenn er nur halb gefüllt ist?
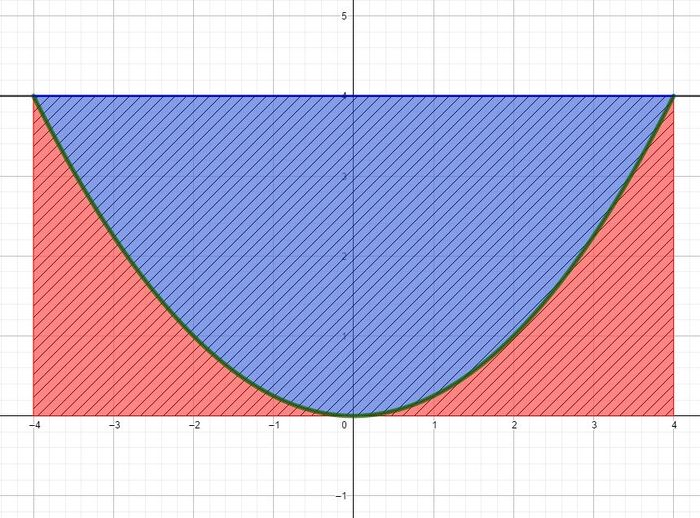
Es gibt 2 Möglichkeiten, um den Inhalt der Querschnittsfläche des Kanal zu berechnen.
- Du berechnest das Integral von der Funktion f mit den Grenzen -4 und 4. Weiter berechnest du den Flächeninhalt des Rechtecks (schraffiert, siehe nachfolgende Abbildung). Abschließend subtrahierst du die Fläche des Integrals (Rot) von der des Rechtecks.
- Du erstellst eine zweite Funktion
, welche den Wasserstand im Kanal wiederspiegelt. Anschließend berechnest du das Integral von g-f mit den Grenzen -4 und 4.
- zu a)
- zu b)
A: Die Querschnittsfläche des Kanals
- zu c)
A: Es befinden sich
Wasser im Kanal, wenn er komplett gefüllt ist.
- zu d)
A: Wenn der Kanal nur halb gefüllt ist, befinden sich ca. 35% der maximalen Wassermenge im Kanal.
Ordne den Funktionen ihre passende Stammfunktion zu. Ermittel dabei die Stammfunktion auf einem Zettel und ordne anschließend richtig zu.
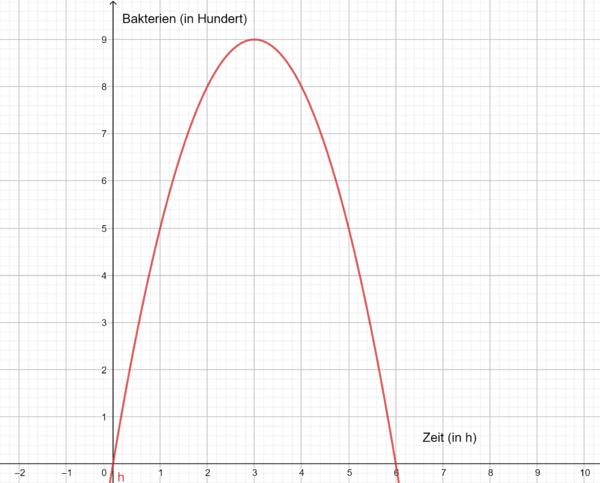
Die Funktion gibt die Wachstumsrate von Bakterien an,
in Stunden,
in Hundert Bakterien (siehe Figur 1). Zu Beginn waren 200 Bakterien vorhanden.
- a) Wie lautet die Funktion
, die die vorhandene Anzahl von Bakterien zum Zeitpunkt
angibt?
- b) Wie viele Bakterien existieren nach 4 Stunden und nach 6 Stunden?
- a)
- b)
Knobelaufgaben
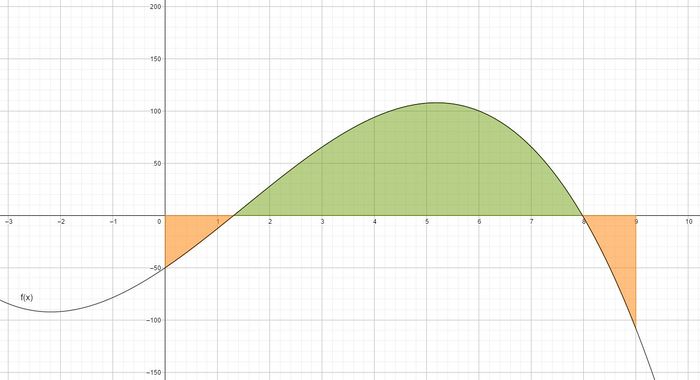
Ein Technik-Unternehmen hat ein neues Smartphone auf den Markt gebracht. Nach 9 Monaten will das Unternehmen prüfen, wie lukrativ das neue Handy in den ersten 9 Monaten war. Der monatliche Gewinn, der durch das Smartphone eingespielt wurde, kann durch die folgende Funktion dargestellt werden:

Die x-Achse gibt die Anzahl der Monate an und die y-Achse den Gewinn in Millionen (€).
- a) Berechne den Ertrag, den das Unternehmen in den ersten 2 Monaten durch das Smartphone einspielt hat.
- b) Berechne den Ertrag nach den ersten 7 Monaten.
- c) Berechne den Ertrag nach den kompletten 9 Monaten.
- d) In welchem Zeitraum erbringt das Smartphone ausschließlich Gewinn für das Unternehmen? Wie viel wird in dem Zeitraum eingenommen?
- e) Interpretiere die Ergebnisse aus den Aufgaben a), b), c) und überlege dir mögliche Begründungen für den erzielten Betrag. Sollte das Smartphone weiterhin produziert werden?
Hier sollst du dir Gedanken machen, ob einerseits deine Ergebnisse aus den vorherigen Aufgaben Sinn ergeben (solltest du natürlich nach jeder Aufgabe machen), und anschließend deine eigenen Begründungen der Ergebnisse festhalten. Zum Bespiel, könnte der anfängliche Verlust mit höheren Produktionskosten als Verkaufseinnahmen begründet werden (warum? plausible Begründung).
Zur Überlegung, ob es lukrativ ist, das Smartphone weiterhin zu produzieren, solltest du dir den Gewinn bzw. Verlust der gesamten 9 Monate anschauen und natürlich den Verlauf der Funktion, die die Einnahmen wiederspiegelt.- zu a)
- zu b)
- zu c)
- zu d)
- zu e) Das Smartphone sollte nicht weiter produziert werden, da durch die gegebene Funktion absehbar ist, dass es schon nach ca. 8 Monaten erneut Verluste für das Unternehmen einspielt.
Bei einem Sprint über 100m treten zwei Läufer gegeneinander an.
Läufer A sprintet mit der Geschwindigkeitsfunktion .
Läufer B sprintet mit der Geschwindigkeitsfunktion
.
ist jeweils die Zeit in Sekunden ab dem Start des Laufes und
die Geschwindigkeit der
Läufer in Meter pro Sekunde.
- a) Geben sie die Funktionen an, die die zurückgelegte Strecke zum Zeitpunkt
angibt.
- b) Zeige, dass Läufer A ungefähr 9,8 Sekunden benötigt.
- c) Bestimme den Wert von c so, dass der Läufer nach 9,69 Sekunden ins Ziel kommt.
- d) Wie viel Meter sind die beiden Läufer nach 5 s von einander entfernt, wenn r dem in c) ermittelten Wert entspricht?
- a)
;
- b)
- c)
- d)
--> Die Läufer sind 4,3 m voneinander entfernt.