Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung

Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Testseite

Monotonie

Merksatz

Das Monotonieverhalten einer Funktion

…beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.

Sei $f(x)$ eine Funktion und $x_1<x_2$

-      Falls auf einem Intervall $f(x_1) < f(x_2)$ gilt, so ist die Funktion streng monoton steigend

-      Falls auf einem Intervall $f(x_1) \leq \ f(x_2)$ gilt, so ist die Funktion monoton steigend

-      Falls auf einem Intervall $f(x_1) > f(x_2)$ gilt, so ist die Funktion streng monoton fallend

-      Falls auf einem Intervall $f(x_1) \geq \ f(x_2)$ gilt, so ist die Funktion monoton fallend

Aufgabe 1

So berechnest du das Monotonieverhalten einer Funktion

1. Erste Ableitung berechnen

2. Nullstellen der ersten Ableitung berechnen

3. Intervalle benennen

4. Monotonietabelle aufstellen

5. Vorzeichen der Intervalle berechnen

6. Ergebnis interpretieren

Beispiel: Monotonieverhalten für $g(x)=x^2$ bestimmen

Zuerst berechnen wir die Ableitung $g'(x)=2x$. Anschließend berechnen wir die Nullstellen der Ableitung ($g'(x)=0$) und erhalten durch Umformungen als Nullstelle $x=0$.

Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten $(-\infty,0)$ und $(0,+\infty)$. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle:

	$-\infty < x < 0$	$f'(0)$	$0 < x < \infty$
$f'(x)$	$< 0$	$= 0$	$> 0$
$G_{f}$	$\searrow$	Tiefpunkt	$\nearrow$

Aus dem Ergebnis können wir schließen, dass die Funktion für $(-\infty,0)$ streng monoton fallend und für $(0,+\infty)$ streng monoton steigend ist.

Aufgabe 2

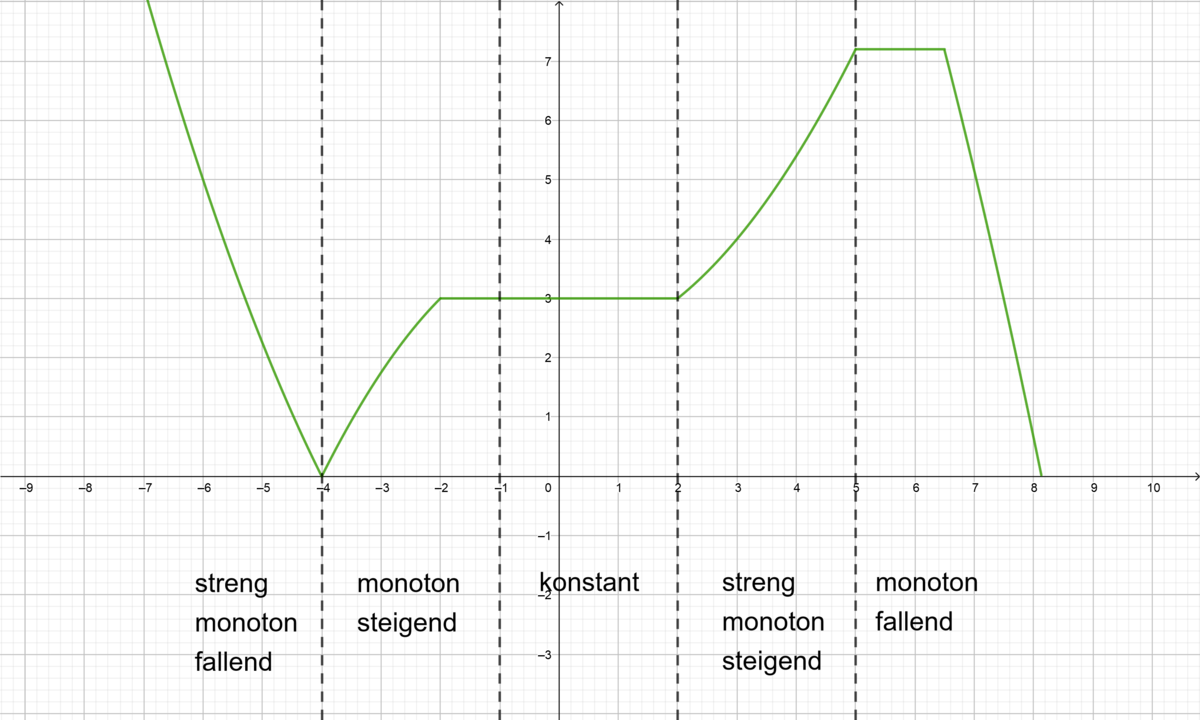
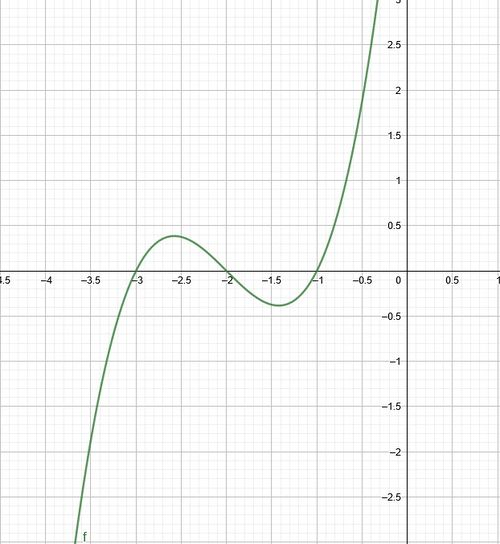
a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion $f'(x)$. Welche Aussagen kannst du über das Monotonieverhalten von $f(x)$ machen?

Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir $f'(x)=0$?

Die Nullstellen von $f'(x)$ definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von $f$ verschieden ist. Nun kannst du betrachten, auf welchen Intervallen $f'(x)$ $<0$ bzw. $>0$ ist. Welche Aussagen kannst du damit über das Monotonieverhalten von $f(x)$ machen?

Die Nullstellen von $f'(x)$ sind $x_1=-3, x_2=-2$ und $x_3=-1$.

Damit sind die zu betrachtenden Intervalle $(-\infty, -3)$, $(-3, -2)$, $(-2, -1)$ und $(-1, +\infty)$. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob $f'(x)$ an diesen $<0$ oder $>0$ ist.

Für $(-\infty, -3)$ ist $f'(x)<0$, somit ist $f(x)$ auf diesem Intervall streng monoton fallend.

Für $(-3, -2)$ ist $f'(x)>0$, somit ist $f(x)$ auf diesem Intervall streng monoton steigend.

Für $(-2, -1)$ ist $f'(x)<0$, somit ist $f(x)$ auf diesem Intervall streng monoton fallend.

Für $(-1, +\infty)$ ist $f'(x)>0$, somit ist $f(x)$ auf diesem Intervall streng monoton steigend.

b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen $f(x)$ mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.

Dein Graph könnte in etwa so aussehen:

Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen.

Verhalten im Unendlichen und nahe Null

Merke

Das Verhalten einer Funktion $f$ im Unendlichen beschreibt, wie sich der Funktionswert $f(x)$ verhält, wenn $x$ gegen $\pm\infty$ geht, also für sehr große positive und negative Werte von $x$. Bei ganzrationalen Funktionen der Form $f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0$ kann man das Verhalten im Unendlichen untersuchen, indem man sich den Summanden des Funktionsterms mit dem größten Exponenten von $x$ anschaut. Betrachte also $g(x)=a_n x^n$. Im Unendlichen verhalten sich $f$ und $g$ gleich, du musst also nur das Verhalten im Unendlichen von $g$ untersuchen. Es gibt vier Fälle, die du dabei unterscheiden musst:

$n$ gerade	$n$ ungerade
$n$ gerade und $a_n>0$: $f$ verläuft "von links oben nach rechts oben", $f(x)\rightarrow \infty$ für $x\rightarrow\pm\infty$	$n$ ungerade und $a_n>0$: $f$ verläuft "von links unten nach rechts oben", $f(x)\rightarrow -\infty$ für $x\rightarrow -\infty$, $f(x)\rightarrow \infty$ für $x\rightarrow\infty$
$n$ gerade und $a_n<0$: $f$ verläuft "von links unten nach rechts unten", $f(x)\rightarrow -\infty$ für $x\rightarrow\pm\infty$	$n$ ungerade und $a_n<0$: $f$ verläuft "von links oben nach rechts unten", $f(x)\rightarrow \infty$ für $x\rightarrow -\infty$, $f(x)\rightarrow -\infty$ für $x\rightarrow\infty$

Merke

Das Verhalten einer Funktion $f$ nahe Null beschreibt, wie sich der Funktionswert $f(x)$ verhält, wenn $x$ gegen Null geht, also für sehr kleine Werte von $x$. Eine ganzrationale Funktion der Form $f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0$ verhält sich nahe Null wie die Summe aus dem absoluten Glied $a_0$ und dem Summanden mit der geringsten Potenz von x, die im Funktionsterm auftaucht.

Beispiel 1

$f(x)=5x^2-3x+4$ verhält sich im Unendlichen wie $g(x)=5x^2$. Für $x\rightarrow -\infty$ geht $f(x)\rightarrow\infty$ und für $x\rightarrow \infty$ geht $f(x)\rightarrow\infty$, da $n=2$ eine gerade Zahl ist und $a_n=5>0$. Nahe Null verhält sich $f$ wie $h(x)=-3x+4$. Wenn man sich ein kleines Intervall um $x=0$ anschaut, sieht der Graph von $f$ dort lokal also aus wie eine Gerade mit der Steigung -3 und dem y-Achsenabschnitt 4. Der y-Achsenabschnitt von $f$ ist daher auch 4.

Beispiel 2

$f(x)=x^5+4x^2-7$ verhält sich im Unendlichen wie $g(x)=x^5$. Für $x\rightarrow -\infty$ geht $f(x)\rightarrow -\infty$ und für $x\rightarrow \infty$ geht $f(x)\rightarrow\infty$, da $n=5$ eine ungerade Zahl ist und $a_n=1>0$ . Nahe Null verhält sich $f$ wie $h(x)=4x^2-7$, also wie eine um den Faktor 4 gestreckte, nach oben geöffnete Parabel mit dem Scheitelpunkt (und y-Achsenabschnitt) bei $(0,-7)$.

Aufgabe 1: Quiz zum Verhalten im Unendlichen

Öffne das Quiz im Vollbildmodus und wähle die jeweils richtigen Antworten aus. Es können eine oder mehrere Antworten richtig sein. Es kann helfen, dir Notizen zu machen.

Aufgabe 2*: Beschreibe das Verhalten

Beschreibe in deinem Heft das Verhalten der nachfolgenden Funktionen und Funktionenscharen im Unendlichen. Gehe dazu vor wie in der Merkbox oben.

a) $f(x)=x^2-\frac{4}{3}x^2-3x+9$

Beachte, dass du manchmal den Funktionsterm erst zusammenfassen musst.

$f$ verhält sich im Unendlichen wie $g(x)=-\frac{1}{3}x^2$. Da $n=2$ eine gerade Zahl ist und $a_n=-\frac{1}{3}<0$, geht $f(x)\rightarrow-\infty$ für $x\rightarrow \pm\infty$. Der Graph von $f$ verläuft also von links unten nach rechts unten.

b) $f_a(x)=-7x^5+ax^3$

Gehe bei Funktionenscharen genau so vor wie bei normalen Funktionen.

$f_a$ verhält sich im Unendlichen wie $g(x)=-7x^5$. Da $n=5$ eine ungerade Zahl ist und $a_n=-7<0$, geht $f(x)\rightarrow\infty$ für $x\rightarrow -\infty$ und $f(x)\rightarrow-\infty$ für $x\rightarrow \infty$. Der Graph von $f$ verläuft also von links oben nach rechts unten.

c) $f_a(x)=-ax^3+2x^2+3x-\frac{4}{7}$ mit $a<0$

Überlege dir zunächst, welches Vorzeichen $a_n$ hat, wenn $a$ negativ ist.

$f_a$ verhält sich im Unendlichen wie $g_a(x)=-ax^3$. Da $n=3$ eine ungerade Zahl ist und $a_n=-a>0$, da $a<0$ ist, geht $f(x)\rightarrow-\infty$ für $x\rightarrow -\infty$ und $f(x)\rightarrow\infty$ für $x\rightarrow \infty$. Der Graph von $f$ verläuft also von links unten nach rechts oben.