Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse

SEITE IM AUFBAU

zurück zur Seite der Herta-Lebenstein-Realschule

1 Quadratische Funktionen entdecken
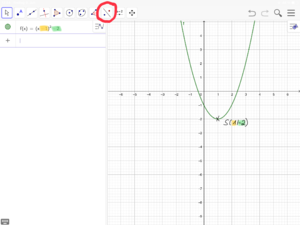
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
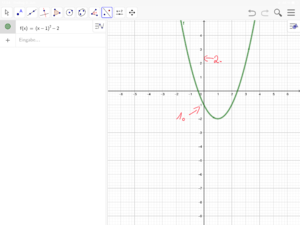
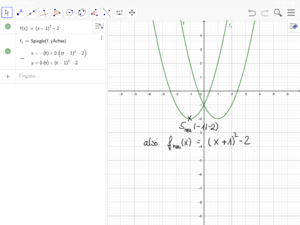
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen

4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c

f(x) = ax² + c Bedeutung des Parameters c

Untersuche die Bedeutung des Parameters c in der Gleichung f(x) = ax² + c mithilfe der Geometriesoftware GeoGebra.

Gib im Algebrafenster die Gleichung f(x) = x² ein. Es wird die Normalparabel gezeichnet.
Erstelle einen Schieberegler a.
Erstelle einen Schieberegler c.
Gib im Algebrafenster die Gleichung f(x) = ax² + c ein. Verändere den Wert von c mithilfe des Schiebereglers. (Die Bedeutung des Parameters a hast du schon erarbeitet.)
Wie verändert sich die Parabel? Notiere deine Beobachtungen.

Link zu GeoGebra

Falls du die Schieberegler nicht erstellen kannst, nutze das nachfolgende Applet.

Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c

Der Graph der Funktion f(x) = ax² + c ist eine Parabel mit dem Scheitelpunkt S(0|c). Der Faktor a bestimmt die Öffnung und Form der Parabel, der Summand c verschiebt den Scheitelpunkt entlang der y-Achse.

Übung 6

Löse die Aufgaben aus dem Buch

S. 13 Nr. 8
S. 14 Nr. 10
S. 14 Nr. 13
S. 14 Nr. 14
S. 14 Nr. 16 (Kontrolliere mit GeoGebra)

"Punktprobe"!

Setze die Koordinaten der Punkte in die Funktionsgleichungen ein und prüfe, ob eine wahre (w) Aussage oder falsche (f) Aussage entsteht. Demnach liegt der Punkt auf der Parabel bzw. nicht auf der Parabel.

Bilderfolge zu GeoGebra: