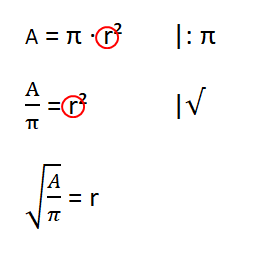Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisfläche
SEITE IM AUFBAU!!
Kreisfläche A
Du hast jeweils den Durchmesser der Pizzen gegeben, damit kannst du den Radius berechnen.
Um die Frage zu beantworten, musst du den Flächeninhalt der Pizzen berechnen können.

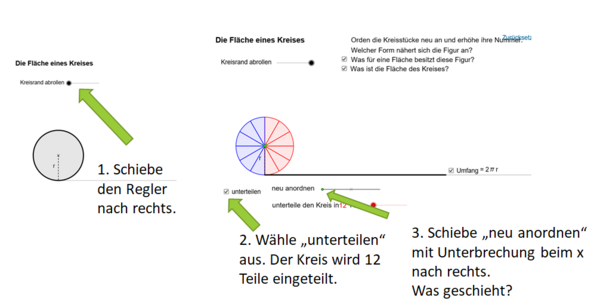
Applet von Anthony Or. Education Bureau
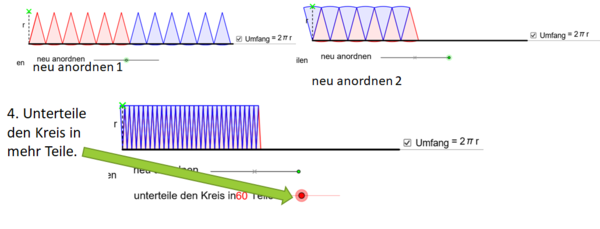
Das Applet ist einfacher dargestellt und gibt bei er neu entstandenen Figur die Längen an. Kannst du nun eine Formel für den Flächeninhalt herleiten?

Die Fläche, die durch das Einteilen des Kreises und das Umlegen entsteht, hat annähernd die Form eines Rechtecks mit den Seitenlängen a= (halber Umfang) und b = r (Radius)
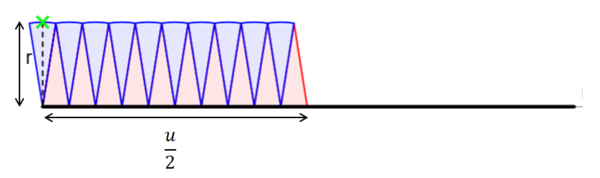

A = a·b | Setze für a den halben Umfang und für b den Radius ein.
= · r | Setze für u die Formel für den Umfang ein: u =2πr.
= · r | Kürze mit 2.
= πr · r | Fasse r·r zusammen.
Das Video fasst die Herleitung der Formel zusammen:
Eine weitere Möglichkeit, den Flächeninhalt eines Kreises abzuschätzen, zeigt das folgende Applet von Pöchtrager:
Beschreibe!

Merke dir die Formel mit dem Lied von Dorfuchs:
Beispiele:
geg: r = 3,0 cm
ges: A
A = π · r² |Wert einsetzen
= π · 3,0²
geg: d = 5,0 cm
ges: A
r = = = 2,5 (cm)
A = π · r² |Wert einsetzen
= π · 2,5²
geg: A = 7,0 cm²
ges: r
A = π · r² |: π
= r2 |
= r &nbap; |Wert einsetzen
= r
1,5 (cm) ≈ r
geg: A = 18,10 cm²
ges: d
d = 2·r; Berechne zunächst r:
A = π · r² |: π
= r2 |
= r &nbap; |Wert einsetzen
= r
2,4 (cm) ≈ r
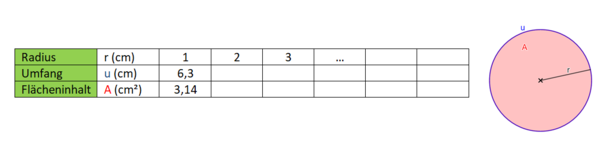
Radius r und Umfang u:
Wenn man den Radius r eines Kreises verdoppelt, verdreifacht, vervierfacht,... dannverdoppelt, verdreifacht, vervierfacht sich der Umfang u.
Radius r und Flächeninhalt A:
Wenn man den Radius r eines Kreises verdoppelt, verdreifacht, vervierfacht,... dannvervierfacht, verneunfacht, versechzehnfacht sich der Flächeninhalt A.