Digitale Werkzeuge in der Schule/Trainingsfeld Ableitungen/Von der mittleren zur lokalen Änderungsrate

Von der mittleren zur lokalen Änderungsrate

Dieser Lernpfad beschäftigt sich mit der mittleren und lokalen Änderungsrate.

• In Aufgabe 1 kannst du die Berechnung der mittlere Änderungsrate anhand von Rechenbeispielen ohne Sachzusammenhang wiederholen. Diese Aufgabe ist eine Förderaufgabe.

• In Aufgabe 2 übst du die Berechnung der mittleren Änderungsrate im Sachkontext. Diese Aufgabe ist eine Förderaufgabe. Wenn du schon sicher bei der Berechnung von mittleren Änderungsraten bist, kannst du Aufgabe 1 und 2 auch überspringen.

• In Aufgabe 3 beschäftigst du dich mit der Unterscheidung der mittleren und lokale Änderungsrate. In den Teilaufgaben a) und b) geht es darum, festzustellen, wie sich die beiden Änderungsraten unterscheiden. Dies ist eine Förderaufgabe.

• In Aufgabe 4 musst du im Sachzusammenhang unterscheiden, welche der beiden Änderungsraten berechnet werden soll. Diese Aufgabe ist eine Förderaufgabe.

• Den Zusammenhang von mittlerer und lokaler Änderungsrate erarbeitest du in Aufgabe 5. Dies ist eine Förderaufgabe.

• In Aufgabe 6 geht es um die geometrischen Zusammenhänge. Dies ist eine Forderaufgabe.

Viel Spaß beim Bearbeiten! :)

Die wichtigsten Begriffe dieses Kapitels

Bevor du mit den Aufgaben beginnst, sind hier schonmal die wichtigsten Begriffe dieses Kapitels in Merkkästchen erklärt. Wenn du dir während der Bearbeitung der einzelnen Aufgaben unsicher bist, kannst du sie dir immer wieder anschauen, um dich zu erinnern. Falls du schon sicher im Umgang mit den folgenden Begriffen bist, kannst du sie zu Anfang auch einfach überlesen und direkt mit den Aufgaben beginnen.

Die mittlere Änderungsrate und wie man sie berechnet

Die mittlere Änderungsrate einer Funktion $f$ in einem Intervall $[x_0, x_1]$ gibt die durchschnittliche Veränderung der Funktionswerte von $f$ in diesem Bereich an. Anders gesagt gibt die mittlere Änderungsrate die Steigung der Sekanten an, die die Punkte $(x_0, f(x_0))$ und $(x_1, f(x_1)))$ verbindet.

Die mittlere Änderungsrate in einem Intervall $[x_0, x_1]$ berechnet man so: $\frac {f(x_1)-f(x_0)} {x_1-x_0}$.

Der Ausdruck $\frac {f(x_1)-f(x_0)} {x_1-x_0}$ wird auch Differenzenquotient genannt.

Die lokale Änderungsrate und wie man sie berechnet

Die lokale Änderungsrate einer Funktion $f$ gibt die Steigung in einem Punkt an. Anders gesagt, gibt die lokale Änderungsrate die Steigung der Tangente an der Stelle $x$ an. Die Steigung der Tangente entspricht der Ableitung der Funktion $f$. Somit lässt sich die lokale Änderungsrate mit Hilfe der Ablteitung $f'(x)$ berechnen. Eine weitere Methode zur Bestimmung der lokalen Änderungsrate ist, den Grenzwert des Differenzenquotienten zu bilden.

Der Grenzwert von $\frac{f(x+h)-f(x)} {h}$ für h gegen 0 heißt Differenzialquotient.

Sekante

Eine Sekante ist eine Gerade zwischen zwei Punkten. Ihre Steigung heißt Sekantensteigung und gibt die mittlere Änderungsrate zwischen diesen beiden Punkten an.

Tangente

Eine Tangente ist eine Gerade, die eine Kurve in einem bestimmten Punkt berührt. Dort haben die Kurve und die Tangente dieselbe Steigung. Diese Steigung entspricht der Ableitung der Funktion in diesem Punkt.

Berechnung der mittleren Änderungsrate

1. Berechnung der mittleren Änderungsrate

Berechne jeweils die durchschnittliche Änderungsrate der Funktionen f, g und h in dem angegebenen Intervall auf einem separaten Blatt Papier. Prüfe im Anschluss die von dir errechneten Werte, indem du sie in die dafür vorgesehenen Kästchen unter der Aufgabe eingibst.

a)$f(x)=4x+2$ im Intervall $[2,5]$

b)$g(x)=x^2$ im Intervall $[2,7]$

c)$h(x)=x^3-2$ im Intervall $[-2,1]$

Wie man die mittlere Änderungsrate in einem Intervall [x₀, x₁] berechnet, schaue einmal oben im Merkkästchen Die mittlere Änderungsrate und wie man sie berechnet nach.

Achte auf die Vorzeichen!

a) Um die mittlere Änderungsrate von f im Intervall $[2,5]$ zu berechen, benötigst du die Funktionswerte von f an den Intervallgrenzen:$f(2)=4\cdot2+2=10$ und $f(5)=4\cdot5+2=22$

Die mittlere Änderungsrate von f berechnet man so: $\frac {f(5)-f(2)} {5-2}=\frac {22-10} {5-2}= \frac{12} {3}= 4$

Bei g(x) und f(x) kannst du bei der Berechnung der mittleren Änderungsrate nach demselben Prinzip vorgehen.

b) $g(2)=2^2=4$ und $g(7)=7^2=49$

Berechnung der mittleren Änderungsrate: $\frac{g(7)-g(2)} {7-2}=\frac{49-4} {7-2}= \frac{45} {5}= 9$

c) $h(-2)=(-2)^3-2=(-10)$ und $h(1)=1^3-2=(-1)$

Berechnung der mittleren Änderungsrate:$\frac{h(1)- h(-2)} {1-(-2)}= \frac{(-1)-(-10)} {1-(-2)}= \frac{9} {3}= 3$

Berechnung der mittleren Änderungsrate im Sachkontext

2. Berechnung der mittleren Änderungsrate im Sachkontext

Dein Sportverein feiert dieses Jahr seinen 25. Geburtstag. Zu diesem Anlass wird eine Tabelle mit den Mitgliederzahlen der letzten Jahre veröffentlicht (leider gab es vor dem Jahr 2010 keine Statistik über die Anzahl der Mitglieder):

Datei:Diwerspng.PNG

Leider ist der Vorstand wegen der Vorbereitung der Jubiläumsfeier sehr beschäftigt und bittet dich, ihm bei der Beantwortung einiger Fragen zu helfen. Du kannst diese zunächst am besten auf einem separaten Blatt Papier lösen und sie anschließend mit den gegebenen Lösungen vergleichen.

a) Wie viele Mitglieder sind seit 2010 im Durchschnitt pro Jahr in deinem Verein hinzugekommen?

In dieser Aufgabe wird die mittlere Änderungsrate im Intervall $[2010, 2018]$ gesucht. Wenn du nicht mehr weißt, wie du diese berechnen kannst, lies im Merkkästchen Die mittlere Änderungsrate und wie man sie berechnet nach.

Um herauszufinden, wie viele Mitglieder seit 2010 in deinem Verein durchschnittlich pro Jahr hinzugekommen sind, musst du die mittlere Änderungsrate im Intervall [2010, 2018] bestimmen. Wir können sagen, dass f(x) die Funktion ist, die jeder Jahreszahl ab 2010 die Anzahl der Mitglieder in diesem Jahr zuordnet. Dann ist f(2010)=210 und f(2018)=418. Mit diesen Werten kannst du jetzt die mittlere Änderungsrate bestimmen:

$\frac {f(2018)-f(2010)} {2018-2010}= \frac {418-210} {2018-2010}= \frac {208} {8}= 26$

Aus der mittleren Änderungsrate kannst du nun ablesen, dass seit 2010 im Durchschnitt pro Jahr 26 Mitglieder in deinem Verein hinzugekommen sind.

b) Der aktuelle Vorstand arbeitet seit 2016 zusammen. Sein Ziel war eine Steigerung der Mitgliedszahlen. Diese sollte im Mittel größer sein als der durchschnittliche Mitgliederzuwachs in den Jahren davor (also von Beginn der Mitgliedererfassung bis zur Wahl des neuen Vorstands 2016). Ist es Ihnen gelungen ihr Ziel zu erreichen?

Vergleiche die mittlere Änderungsrate in den Jahren vor der Wahl des neuen Vorstands (2010-2016) und nach der Wahl des neuen Vorstands (2016-2018). Wenn du nicht mehr weißt, wie du die mittlere Änderungsrate berechnen kannst, schaue im Merkkästchen Die mittlere Änderungsrate und wie man sie berechnet nach.

Ja, ihnen ist es knapp gelungen ihr Ziel zu erreichen.

Um auf diese Lösung zu kommen, musst du die mittleren Änderungsraten in den Jahren vor und nach der Wahl des neuen Vorstands vergleichen.

durchschnittliche Änderungsrate vor der Wahl: $\frac{f(2016)-f(2010)} {2016-2010}=\frac {365-210} {2016-2010}=\frac {155} {6}=25,83$

durchschnittliche Änderungsrate nach der Wahl: $\frac{f(2018)-f(2016)} {2018-2016}=\frac {418-365} {2016-2010}=\frac {53} {2}=26,5$

Die mittlere Änderungsrate der letzten zwei Jahren ist also höher als die der Jahre davor. Daraus lässt sich schließen, dass der durchschnittliche Mitgliedszuwachs im Verein pro Jahr seit 2016 ein wenig höher ist als es in den Jahren davor der Fall war.

Unterscheidung der Änderungsraten

3. Mittlere Änderungsrate und lokale Änderungsrate

a) Ordne die Karten jeweils richtig zu, indem ihr sie entweder zur mittleren oder lokalen Änderungsrate zieht.

Sieh dir oben das Merkkästchen zur mittleren Änderungsrate nochmal an.

Schau dir das oben aufgeführte Merkkästchen zur lokalen Änderungsrate an.

b) Fertige in deinem Heft eine Tabelle zur mittleren und lokalen Änderungsrate mit den Karten aus Teilaufgabe a) an. Stelle die zueinander passenden Begriffe gegenüber, zum Beispiel Sekante und Tangente.

Hier sollst du Begriffspaare bilden. Das Paar soll aus einem Begriff zur mittleren Änderungsrate und einem Begriff zur lokalen Änderungsrate bestehen. Die Begriffe sollen inhaltlich zueinander passen, wie zum Beispiel das Begriffspaar Sekante (mittlere Änderungsrate) und Tangente (lokale Änderungsrate).

mittlere Änderungsrate	lokale Änderungsrate
Sekante	Tangente
Differenzenquotient	Differenzialquotient
die Steigung zwischen zwei Punkten	die Steigung im Punkt P
die durchschnittliche Steigung	die Ableitung an der Stelle x0
Durchschnittsgeschwindigkeit	die Momentangeschwindigkeit

Änderungsraten im Sachzusammenhang

4. Änderungsraten im Sachzusammenhang

Tim fährt mit dem Fahrrad zur Schule und muss an einer roten Ampel abbremsen. Für den in der Zeit t (in Sekunden) zurückgelegten Weg s(t) (in Metern) gilt:

$s(t)=10t-t^2$ für $t\in [0;5]$

a) Berechne den zurückgelegten Weg nach 3 und 5 Sekunden.

Nach 3 Sekunden hat Tim einen Weg von 21 Metern zurückgelegt, denn $s(3)=10\cdot3-3^2=30-9=21$. Nach 5 Sekunden hat er 25 Meter zurückgelegt, denn es gilt $s(5)=10 \cdot 5-5^2=50-25=25$.

b) Berechne die Geschwindigkeit, die Tim nach 3 Sekunden bzw. nach 5 Sekunden mit seinem Fahrrad erreicht hat.

Gesucht wird die momentane/lokale Geschwindigkeit.

Zur Berechnung der momentanen/lokalen Geschwindigkeit musst du die Ableitung der Funktion bilden.

Die lokale Änderungsrate $s'(t)=10-2t$ entspricht der Geschwindigkeit. $s'(3)=10-2\cdot3=10-6=4$ und $s'(5)=10-2\cdot5=10-10=0$.

c) Warum hat die oben genannte Funktion im vorliegenden Sachzusammenhang für $t=6$ keinen Sinn?

Die angegebene Funktion kann nicht für t=6 gelten, da die gegebene Funktion nur für den Definitionsbereich $t\in [0;5]$ gilt. In der Realität bedeutet es, dass Tim nach 5 Sekunden an der Ampel stehen geblieben ist. Somit ist der Weg, der durch die genannte Funktion beschrieben wird, zu Ende.

Zusammenhang von mittlerer und lokaler Änderungsrate

5. Zusammenhang von mittleren und lokalen Änderungsrate

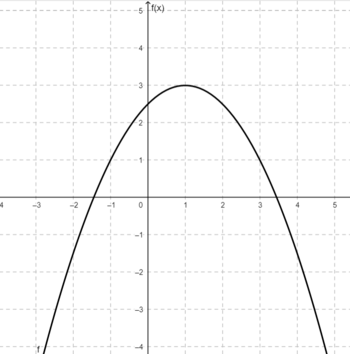
Die Funktion $f(x) = -1/2\cdot(x-1)^2+3$ ist in der folgenden Abbildung dargestellt:

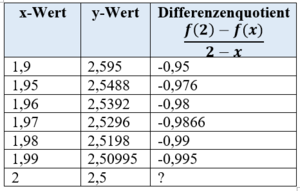
In der folgenden Tabelle siehst du einige Funktionswerte der Funktion f aufgelistet. Außerdem wurden die Differenzenquotienten vom Punkt $P = (2|2,5)$ mit Punkten in der Umgebung ausgerechnet.

a) Beschreibe, was mit dem Differenzenquotient passiert, wenn sich die x-Werte 2 annähern.

Je näher man den x-Wert an 2 annähert, desto kleiner wird der Wert des Differenzenquotienten. Er nähert sich von anfänglich -0,95 immer näher an -1 an. So liegt der Wert des Differenzenquotienten bei 1,99 bei -0,995.

b) Erkläre, warum in der letzten Zeile unter "Differenzenquotient" ein "?" eingetragen ist.

Überlege, welche Werte im Zähler und im Nenner des Differenzenquotienten in dieser Zeile stünden.

In dieser Zeile müsste man durch 0 teilen, da man $\frac {f(2)-f(2)} {2-2} = \frac {f(2)-f(2)} {0}$ rechnen würde. Dies ist keine zulässige Rechenoperation, also nicht berechenbar.

c) Was bedeutet das Ergebnis aus 1) für die durchschnittliche Änderungsrate und was bedeutet es für die momentane Änderungsrate im Punkt $P = (2|2,5)$? Wie hängen diese beiden Begriffe miteinander zusammen? Löse dazu den Lückentext. Dabei beziehen sich die Lücken immer auf $\frac {f(2)-f(x)} {2-x}$.

Der Grenzwert des Differenzenquotienten ist der Differentialquotient $\frac{f(2)-f(x)} {2-x}$ für x gegen 2.

Wenn der Differenzenquotient einen bestimmten Wert, z.B. -0,95 bei x=1,9, annimmt, entspricht der Wert der mittleren Änderungsrate der Funktion im Intervall [1,9;2]. Wenn man kleinere Intervalle betrachtet, nähert sich der Differenzenquotient -1 an. Das bedeutet, in der Umgebung von x=2 liegt die Änderungsrate nahe bei -1. Da die Änderungsrate in einem Punkt von dem Differenzialquotient angegeben wird, entspricht der der Grenzwert des Differenzenquotienten →$\frac{f(2)-f(x)} {2-x}$ dem Differenzialquotienten. Letzterer gibt die lokale Änderungsrate im Punkt $P = (2|2,5)$ an.

Geometrischer Zusammenhang von mittlerer und lokaler Änderungsrate

6. Geometrischer Zusammenhang von mittleren und lokalen Änderungsrate (Forder-Aufgabe)

Im folgenden Applet ist die Funktion $f(x) = 0,2x^2+0,5$ dargestellt. Sieh dir zunächst die Formeln und die Abbildung in der Darstellung an. Durch Verschieben des x₁-x₀-Schiebereglers verändern sich die Werte in den Formeln und die Abbildung. Probier einmal aus, was sich verändert.

a) Was gibt die Variable m_s an?

m ist dir als Steigung einer Geraden bekannt. Wie nennt man die Gerade, deren Steigung hier mit m_s benannt ist?

m_s gibt die Steigung der Sekante durch die Punkte A und B an.

b) Fülle nun den folgenden Lückentext aus.

Verschieben den "x₁-x₀"-Schieberegler in der oberen Darstellung und lies die gesuchten Werte in der Formel zum Differenzenquotienten ab.

Sieh dir oben das Merkkästchen zum Thema Sekante an.

Sieh dir oben das Merkkästchen zum Thema Tangente an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

3)Sekante

4)sinkt

5)die Steigung der Funktion im Punkt $x_0$

6)dem Differentialquotienten

7)0,8