Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
- Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.
Inhaltsverzeichnis
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Gegeben sind eine Ebene und eine Gerade
. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.
1. Schritt: Setze die Geraden- und Ebenengleichung gleich.
2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf.
3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner.
4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene und die Gerade
nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.
5. Schritt: Da sich die Ebene und die Gerade
schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter
in die Geradengleichung ein.
Gegeben ist eine Ebene .
1. Setze die Geradengleichung mit der Ebenengleichung gleich.
2. Stelle ein LGS auf.
3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.
4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.
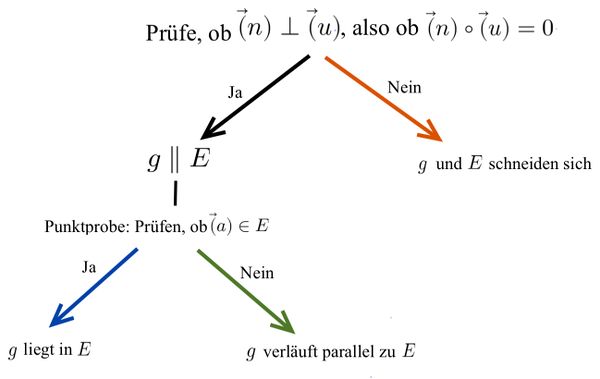
Gegeben sind eine Ebene und eine Gerade
. Bestimme die Lagebeziehung von Gerade und Ebene.
1. Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt:
2. Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt: Der Stützvektor liegt nicht in der Ebene. Daher verlaufen die Gerade
und die Ebene
parallel zueinander.
Gegeben ist eine Ebene .
Bestimme
und
in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist.
a) Die Gerade soll parallel zur Ebene
verlaufen.
.
b) Die Gerade soll in der Ebene
liegen.
Finde zuerst m: .
Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt
sein:
.
c) Die Gerade soll die Ebene
schneiden.
Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene dargestellt. Der Strahl des Laserpointes wird durch die Gerade <
modelliert.
Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft.
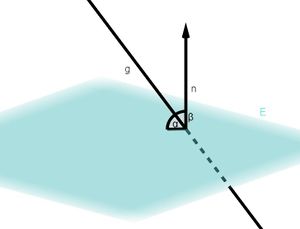
⭐Berechnung des Winkels zwischen Gerade und Ebene
Sei eine Ebene mit dem Normalenvektor
und
eine Gerade mit dem Richtungsvektor
. Der Schnittwinkel
zwischen
und
kann mit folgender Formel berechnet werden:
Wenn du wissen möchtest, warum du nicht wie beim Winkel zwischen zwei Geraden den Kosinus benutzt, kannst du das hier nachlesen:
Gegeben sind die Gerade und die Ebene
. Bestimme den Winkel unter dem sich die Gerade
und die Ebene
schneiden.
1. Schritt: Notiere den Richtungvektor der Gerade und den Normalenvektor
der Ebene.
und
.
2. Schritt: Setze die Vektoren in die Formel ein.
3. Schritt: Umformen der Gleichung
Eine Gerade soll die
in einem Winkel von
schneiden. Über die Gerade
ist nur bekannt, dass sie im Punkt
beginnt und sie in Richtung des Vektors
verläuft. Stelle die Gerade
auf.
Lagebeziehung Ebene-Ebene
Basiswissen
Seien E und F zwei Ebenen im Raum. Um die Lagebeziehung dieser Ebenen zu untersuchen, müssen eine Reihe bestimmter Rechenschritte durchgeführt werden:
Schritt 1: Die beiden Ebenengleichungen gleichsetzen
Schritt 2: LGS interpretieren
Schritt 3: Schnittgerade bestimmen
Interpretiere die jeweilige Situation geometrisch.
a)
b)
c)
Untersuche die Lagebeziehung der jeweiligen Ebenen.
a)
b)
c)
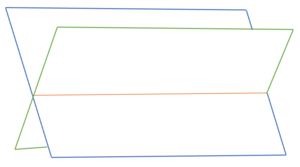
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen und
. Berechne die Geradengleichung der oberen Zeltkante.
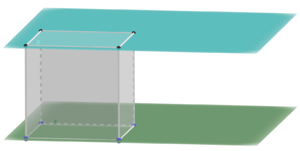
⭐Berechnung des Winkels zwischen Ebene und Ebene
Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene und die Rückenlehne durch die Ebene R
beschrieben werden kann.
a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob die auf die neue Bank zutrifft.
Als Normalenvektor der Ebene erhält man
und als Normalenvektor der Ebene
.
Einsetzen in die Formel liefert:
Umstellen der Formel ergibt:
b) Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene und die Rückenlehne der Ebene
Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen.
Es soll der Winkel zwischen den beiden Rückenlehnen und
berechnet werden.
Die Normalenvektoren der Ebenen lauten und
.
Einsetzen in die Formel liefert:
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle cos(\beta)=\frac{ | \left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right) \ast \left( \begin{matrix} 0\\ -1\\ -0,4 \end{matrix} \right)|}{|\left( \begin{matrix} 0\\ -1\\ 0,4 \end{matrix} \right)| \cdot | \left( \begin{matrix} 0\\ -1\\ -0,4 \end{matrix} \right)|} \Leftrightarrow cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow cos(\bata)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow cos(\beta)=\frac{21}{29}}
Umstellen der Formel ergibt: