Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Zinseszins

Info

In diesem Abschnitt lernst du mit dem Zinseszins umzugehen. Der Zinseszins tritt auf, wenn du dein Geld mehrere Jahre auf deinem Konto lässt und jedes Jahr aufs Neue Zinsen bekommst und diese Zinsen auch auf deinem Konto lässt. Dann erhältst du nämlich auf das Geld, dass du durch die Zinsen bekommst wieder neue Zinsen - den Zinseszins.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg!

Beispiel

Hervorhebung1

Aufgabe 1: Vergleich Zins und Zinseszins

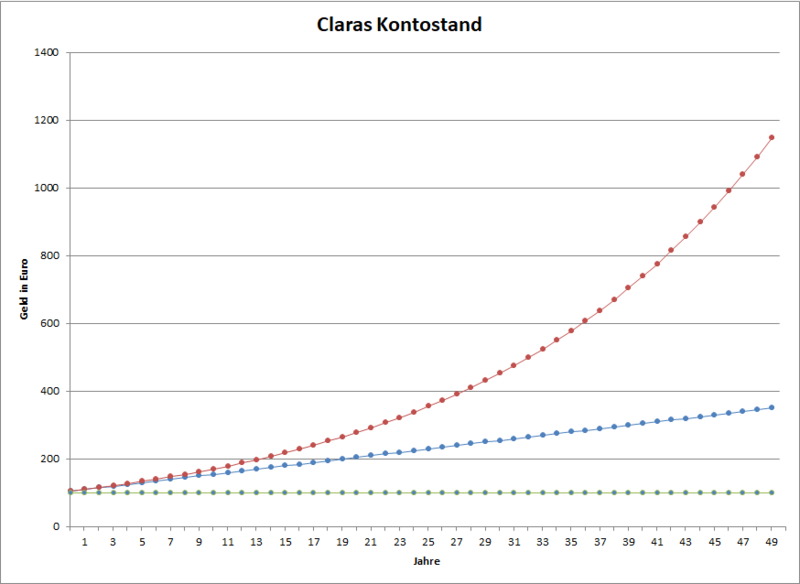
Hier ist ein Diagramm von der Entwicklung von Claras Kontostand aus dem Beispiel für $50$ Jahre dargestellt. 

a) Ordne den Graphen die verschiedenen Entwicklungen zu.

b) Was fällt dir bei der Betrachtung der verschiedenen Verläufe der Graphen auf? Was bedeuten diese Auffäligkeiten für Claras Kontostand?

roter Graph	Entwicklung mit Zinseszins
blauer Graph	Entwicklung mit Zinsen ohne Zinseszins
grüner Graph	Entwicklung ohne Zinsen

Schaue dir vor allem die Unterschiede zwischen der Entwicklung mit Zinseszinsen und der Entwicklung mit Zinsen, aber ohne Zinseszinsen an. Was bedeuten die Abstände zwischen den Graphen für Claras Kontostand?

Hier gibt es kein richtig oder falsch. Dir ist bestimmt viel Unterschiedliches aufgefallen.

Hier sind nur einige Auffälligkeiten:

Am Anfang sind der rote und der blaue Graph fast gleich, erst ab etwa $10$ Jahren gibt es nennenswerte Unterschiede. Das bedeutet, dass es für die ersten Jahre fast keinen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfache Zinsen.

Ab $10$ Jahren wird der Unterschied zwischen dem blauen und den roten Graphen immer größer. Das bedeutet, dass es langfristig einen erheblichen Unterschied macht, ob Clara Zinseszins bekommt oder nur einfachen Zins.

Der Unterschied zwischen dem blauen und roten Graphen wird mit den Jahren immer schneller größer. Das bedeutet: Je länger Clara spart, desto mehr Gewicht hat der Zinseszins gegenüber dem einfachen Zins.

Aufgabe 2: Rechnen mit und ohne Zinseszins

Maja hat inzwischen $900$€ gespart. Sie ist 13 Jahre alt und möchte dieses Geld für ihren Führerschein anlegen. Sie bekommt von der Bank 6% Zinsen pro Jahr. Ein Führerschein kostet ungefähr $1125$ €.  

a) Hat Maja mit 17 Jahren genügend Geld auf ihrem Konto, um den Führerschein zu bezahlen?

Du kannst die Zinsen des ersten Jahres ausrechnen und dann das Geld, dass Maja jetzt hat als neues Startkapital nehmen und so die Zinsen für das zweite Jahr ausrechnen. Dann kannst du das wiederholen bis du in dem Jahr angekommen bist, wo du hin möchtest.

Ein schrittweises Vorgehen hilft.

Du kannst damit beginnen auszurechnen wieviel Geld Maja nach einem Jahr hat. Dieses errechnete Geld ist dann das Kapital für das zweite Jahr, so kannst du das zweite Jahr berechnen und bekommst dann das Kapital für das dritte Jahr raus. Du kannst das so lange fortführen, bis Maja $17$ Jahre alt ist.

Maja hat mit 17 Jahren genügend Geld auf ihrem Konto für den Führerschein. Nach einem Jahr hat sie $954$€, nach zwei Jahren $1011{,}24$€, nach drei Jahren$1071{,}94$€ und nach vier Jahren dann $1136{,}23$ €.

b) Wieviel Geld hätte Maja mit 17 Jahren, wenn sie statt $6$% nur $4$% Zinsen bekommen würde?

Wo liegt der Unteschied zu Aufgabe 2 a)?

Diese Aufgabe kannst du genauso Lösen wie Aufgabe 2 a), nur der Wert für $p$ und damit auch der für $Z$ ist anders.

Maja hätte nach einem Jahr $936$€, nach zwei Jahren $973{,}44$€, nach drei Jahren$1012{,}38$€ und nach vier Jahren dann $1052{,}87$ € auf ihrem Konto.

c) Wie lange müsste Maja warten, bis sie ihren Führerschein bei $4$% Zinsen bezahlen könnte?

Reicht ihr Geld mit $17$ Jahren? Wie ist es mit $18$ oder $19$ Jahren?

Du kannst dein Ergebnis aus Aufgabe 2 b) verwenden und dann wie in der Aufgabe 2 b) weiterrechnen bis Maja genügend Geld für ihren Führerschein beisammen hat.

Maja hätte mit $17$ Jahren erst $1052{,}87$ € auf ihrem Konto. Mit$18$ Jahren hätte sie dann $1094{,}99$€ und mit $19$ Jahren dann $1138{,}79$ € auf ihrem Konto. Der Führerschein kostet ungefähr $1125$ €, somit müsste Maja $6$ Jahre lang warten bis sie genügend Geld für den Führerschein beisammen hat.

d) Maja überlegt, ob sie das Geld, das sie jedes Jahr an Zinsen bekommt immer abheben soll und in ihre Spardose wirft. Was würdest du ihr raten?

Ändert das etwas an den Zinsen, die Maja bekommt?

Auf welches Geld bekommt Maja dann jedes Jahr Zinsen? Wieviel Zinsen würde sie dann jedes Jahr bekommen? Was bedeutet das für ihren Führerschein?

Es gibt hierfür keine eindeutige Lösung. Hier ist eine mögliche Argumentation. Du hast jedoch möglicherweise eine andere gute Argumentation gefunden: Wenn Maja das so macht, dann würde sie jedes Jahr nur auf ihre $900$ € Zinsen bekommen und keine Zinseszinsen. Sie würde bei Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 6%} dann jedes Jahr $54$ € bekommen. Nach vier Jahren hätte Maja $1116$€. Das würde nicht für den Führerschein reichen.

Erweiterung der Zinsformel

Die Zinsformel kann auch für die Berechnung des Zinseszins genutzt werden: $K=100$ € werden mit einem Zinssatz $p=5$ % vier Jahre lang gespart. $K_1$ bezeichnet das Kapital nach einem Jahr, $K_2$ nach zwei Jahren und so weiter. Damit ist $K_n$ das Kapital nach $n$ Jahren.

Für das erste Jahr gilt $K\cdot(1 + 1\cdot \frac{z}{100}) = K_1$ Für $K = 100$€ folgt dann $100$€$\cdot(1 + 1\cdot \frac{z}{100}) = 105$€.

Für das zweite Jahr gilt dann $K_1\cdot(1 + 1\cdot \frac{z}{100}) = K_2$ $= 105$€$\cdot(1 + 1\cdot \frac{z}{100}) = 110{,}25$€.

Das kann auch in einem Rechenschritt vereinfacht werden:

Jetz setzen wir für das Kapital nach einem Jahr $K_1$. die Formel für das erste Jahr $K\cdot(1 + 1\cdot \frac{z}{100}) = K_1$ ein: $(K_1)\cdot(1 + 1\cdot \frac{z}{100}) = (K\cdot(1 + 1\cdot \frac{z}{100}))\cdot(1 + 1\cdot \frac{z}{100}) = K_2$

Für das dritte Jahr ergibt sich dann

$K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100}) = K_3$

Du kannst für jedes weitere Jahr einmal die Formel mit $\cdot(1 + 1\cdot \frac{z}{100})$ multiplizieren.

Noch kürzer lässt sich das als Potenz schreiben: $K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^2= K_2$

oder für das dritte Jahr

$K\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})\cdot(1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^3= K_3$.

Für ein beliebiges Jahr, das Jahr Nummer $n$ wird dann $K$ insgesamt $n$-mal mit dem Faktor $1 + 1\cdot \frac{z}{100}$ multipliziert:

$K\cdot(1 + 1\cdot \frac{z}{100})\cdot$ ... $n$- mal ...$\cdot (1 + 1\cdot \frac{z}{100})= K\cdot(1 + 1\cdot \frac{z}{100})^n= K_n$.

{{Box | Aufgabe 4: Coronabonus | Detlef arbeitet als Krankenpfleger. Daher hat er einen Corona-Bonus von $1000\euro$ erhalten. Seine Frau ist Professorin, deshalb sind sie als Familie finanziell gut abgesichert. Er möchte deswegen $800\euro$ des Corona-Bonuses sparen.

a) Seine Bankberaterin bei der SparBank sagt ihm: "Bei uns bekommen Sie so viel Zinsen, dass Sie nach vier Jahren schon ungefähr 136 Euro mehr haben." Wie hoch liegt der Zinssatz bei der SparBank?

Manchmal hilft es abzuschätzen und dann auszuprobieren

Die Zinsen bei einer Bank liegen irgendwo zwischen $2$ % und $7$ %. Du kannst dich durch Ausprobieren an die Lösung rantasten.

mögliche Rechnung: $800\cdot(1 + 1\cdot \frac{4}{100})^4= 935{,}89$

Detlef erhällt vier Prozent Zinsen pro Jahr.

b) Detlef entscheidet sich sein Geld bei der SparBank anzulegen. Er erhällt durch den zweiten Lockdown eine weitere Bonuszahlung, sodass er nach vier Jahren schon ungefähr $1170\euro$ hätte. Wie groß ist diese Bonuszahlung?

Wie groß ist der Unterschied zwischen dem Geld nach vier Jahren mit und ohne Bonuszahlung? Was sagt dieser Unterschied über die Bonuszahlung aus?

Aus dem Unterschied zwischen dem Geld nach vier Jahren mit und ohne Bonuszahlung kannst du errechnen wie hoch diese Bonuszahlung ist. Der Unterschied setzt sich nur aus der Bonuszahlung und den Zinsen und Zinseszinsen dieser zusammen.

Mögliche Rechnung: $(800+x)\cdot(1 + 1\cdot \frac{4}{100})^4= 1170$

umstellen nach $x$: $(800+x)= 1170:(1 + 1\cdot \frac{4}{100})^4$ Daraus folgt $x= 1170:(1 + 1\cdot \frac{4}{100})^4-800=200{,}121$

Der zweite Bonus beträgt ungefähr $200$€.

c) Detlef ruft danach noch bei der GrünBank an. Die Bankberaterin der GrünBank unterbreitet ihm folgendes Angebot:" Bei uns können Sie zwischen zwei Angeboten auswählen. Wir können ihnen einerseits das kurzsparer Angebot, bei dem Sie jedes halbe Jahr zwei Prozent Zinsen erhalten anbieten. Sie können alternativ das langsparer Angebot annehmen, bei dem Sie nach 5 Jahren $22$ Prozent Zinsen erhalten, wenn das ihr Geld die vollen fünf Jahre auf ihrem Konto verweilt." Zu welchem Angebot würdest du Detlef raten, um seine $1000$ € bestmöglichst anzulegen? Zur Auswahl stehen das von der Sparbank, das kurzsparer Angebot und das langsparer Angebot der Grünbank?

Wo bekommt er mehr Geld? Gibt es noch andere Aspekte die wichtig sein können?

Du kannst gucken wie groß der Unterschied des Geldes nach einem, zwei und fünf Jahren ist. Was passiert, wenn Detlef das Geld nach 4 Jahren abhebt?

Es gibt nicht die eine richtige Lösung. Hier sind einige mögliche Argumente, aber du hast vielleicht auch andere gute Argumente gefunden:

Bei zwei Prozent Zinsen halbjährlich ist Detlef am flexibelsten, da er nicht ein ganzes bzw. fünf Jahre warten muss um die Zinsen zu bekommen.

Bei zwei Prozent Zinsen alle 6 Monate bekommt er mehr Geld als bei vier Prozent Zinsen jährlich, weil er dann jedes Jahr zwei mal zwei Prozent (also vier Prozent) auf sein Startkapital und dazu am Ende des Jahres schon die die Zinseszinsen des ersten Halbjahres bekommt.

Rechnerischer Vergleich nach fünf Jahren: SparBank:$1000\cdot(1 + 1\cdot \frac{4}{100})^5= 1216{,}65$ GrünBank kurzsparer:$1000\cdot(1 + 1\cdot \frac{2}{100})^{5*2}= 1218{,}99$

GrünBank langsparer:$1000\cdot(1 + 1\cdot \frac{22}{100})= 1220$

d) Die Pflegekräfte leisten sowohl in der Pandemie, als auch in Zeiten ohne Pandemie Herausragendes und werden schlecht bezahlt. Deswegen gibt es zusätzlich zu den Bonuszahlungen eine längst überfällige Lohnerhöhung. Da Detlef nur eine halbe Stelle hat, weil er sich um die Tochter kümmert, bekommt er $15$ Euro zusätzlich im Monat. Diese $15$ Euro spart er zusätzlich zu den $1000$ €. Wieviel Geld hat er jetzt insgesamt nach drei Jahren auf seinem Konto, wenn er bei der SparBank spart?

Aus welchen Teilen setzt sich Detlefs Kontostand am Ende jeden Jahres zusammen?

Detlef zahlt jedes Jahr zusätzliches Geld auf sein Konto zum Sparen ein. Auch für dieses Geld erhält er ab dann Zinsen.

Mögliche Rechnung: nach einem Jahr: $(1000+15\cdot12)\cdot(1 + 1\cdot \frac{4}{100})= 1227{,}2$ nach zwei Jahren: $(1227{,}2+15\cdot 12)\cdot(1 + 1\cdot \frac{4}{100})= 1463{,}49$ nach drei Jahren: $(1463{,}49+15\cdot 12)\cdot(1 + 1\cdot \frac{4}{100})= 1709{,}23$

Detlef hat nach drei Jahren mit der Lohnerhöhung <1709{,}23> € auf seinem Konto

Link zum nächsten Kapitel:

Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung/Abschlussvideo

Link zurück zur Übersicht:

Digitale Werkzeuge in der Schule/Fit für VERA-8/Zinsrechnung