Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Lineare Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 152: | Zeile 152: | ||
{{Lösung versteckt|1 = '''Behälter A: ''' | {{Lösung versteckt|1 = '''Behälter A: ''' | ||
Wir haben die Punkte <math> (0|500)</math> und <math>(15|0)</math> und die allgemeine Funktionsgleichung <math> f(x) = m | Wir haben die Punkte <math> (0|500)</math> und <math>(15|0)</math> und die allgemeine Funktionsgleichung <math> f(x) = m\cdot x+b</math>. In diese setzten wir die beiden Punkte jeweils ein: | ||
'''<math> (0|500)</math>:''' <math> f(0) = m | '''<math> (0|500)</math>:''' <math> f(0) = m\cdot 0+b = 500</math>, wodurch <math>b=500</math> folgt. | ||
'''<math>(15|0)</math>:''' <math>f(15) = m | '''<math>(15|0)</math>:''' <math>f(15) = m\cdot 15+b=0</math>. Da wir schon wissen, dass <math>b=500</math> ist, folgt hieraus, dass <math>m=-\frac{100}{3}</math> ist. | ||
Setzt man nun <math>m</math> und <math>b</math> in die Funktionsgleichung ein, erhalten wir <math> f(x) = -\frac{100}{3} | Setzt man nun <math>m</math> und <math>b</math> in die Funktionsgleichung ein, erhalten wir <math> f(x) = -\frac{100}{3} \cdot x + 500</math>|2=Lösung für Behälter A|3=Lösung für Behälter A}} | ||
{{Lösung versteckt|1 = '''Behälter B: ''' | {{Lösung versteckt|1 = '''Behälter B: ''' | ||
Wir haben die Punkte <math> (0|300)</math> und <math>(20|0)</math> und die allgemeine Funktionsgleichung <math> g(x) = n | Wir haben die Punkte <math> (0|300)</math> und <math>(20|0)</math> und die allgemeine Funktionsgleichung <math> g(x) = n\cdot x+a</math>. In diese setzten wir die beiden Punkte jeweils ein: | ||
'''<math> (0|300)</math>: ''' <math> g(0) = n | '''<math> (0|300)</math>: ''' <math> g(0) = n\cdot 0+a = 300</math>, wodurch <math>a=300</math> folgt. | ||
'''<math>(20|0)</math>:''' <math>g(20) = n | '''<math>(20|0)</math>:''' <math>g(20) = n\cdot 20+a=0</math>. Da wir schon wissen, dass <math>a=300</math> ist, folgt hieraus, dass <math>n=-15</math> ist. | ||
Setzt man nun <math>n</math> und <math>a</math> in die Funktionsgleichung ein, erhalten wir <math> g(x) = -15 | Setzt man nun <math>n</math> und <math>a</math> in die Funktionsgleichung ein, erhalten wir <math> g(x) = -15 \cdot x + 300</math>|2=Lösung für Behälter B|3=Lösung für Behälter B}} | ||
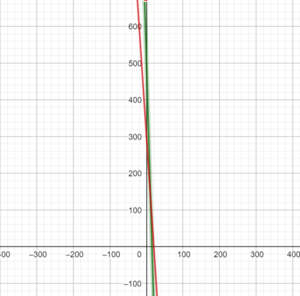
{{Lösung versteckt|1 =[[Datei:Funktionsgraphen.png|mini|Grün: Behälter A, Rot: Behälter B]]|2=Lösung für die Funktionsgraphen|3=Lösung für die Funktionsgraphen}} | {{Lösung versteckt|1 =[[Datei:Funktionsgraphen.png|mini|Grün: Behälter A, Rot: Behälter B]]|2=Lösung für die Funktionsgraphen|3=Lösung für die Funktionsgraphen}} | ||
| Zeile 182: | Zeile 182: | ||
{{Lösung versteckt|1 = Die Variable <math>x</math> steht für unsere Stundenzahl, also setzten wir für <math>x</math> <math> 5</math> ein. | {{Lösung versteckt|1 = Die Variable <math>x</math> steht für unsere Stundenzahl, also setzten wir für <math>x</math> <math> 5</math> ein. | ||
'''Behälter A: ''' Wir berechnen also <math>f(5)=-\frac{100}{3} | '''Behälter A: ''' Wir berechnen also <math>f(5)=-\frac{100}{3} \cdot 5 + 500 =\frac{1000}{3}</math>. Dieser Wert gibt an, wie viel Wasser nach den fünf Stunden noch im Behälter A ist. Um zu berechnen, welche Menge im Napf ist, müssen wir von der Anfangsmenge <math> 500ml </math> die <math> \frac{1000}{3} ml</math> abziehen und erhalten somit, dass ca. <math>167ml</math> in dem Napf sind. Dieser läuft also über. | ||
'''Behälter B: ''' Wir berechnen also <math>g(5)=-15 | '''Behälter B: ''' Wir berechnen also <math>g(5)=-15 \cdot 5 + 300 =225</math>. Dieser Wert gibt an, wie viel Wasser nach den fünf Stunden noch im Behälter B ist. Um zu berechnen, welche Menge im Napf ist, müssen wir von der Anfangsmenge <math> 300ml </math> die <math> 225ml</math> abziehen und erhalten somit, dass ca. <math>75ml</math> in dem Napf sind. Dieser läuft also '''nicht ''' über.|2=Lösung|3=Lösung}} | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
Version vom 29. Mai 2019, 10:06 Uhr
Lineare Funktionen - ein Überblick
Lineare Funktionen erkennen
Lineare Funktionen - Bestimmung von Geradengleichungen
Prüfen, ob Punkte auf einer Geraden liegen
Eine lineare Gleichung einer Geraden zuordnen
Den Schnittpunkt zweier Geraden bestimmen
Lineare Funktionen im Anwendungskontext