Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren/Quadratische Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 28: | Zeile 28: | ||
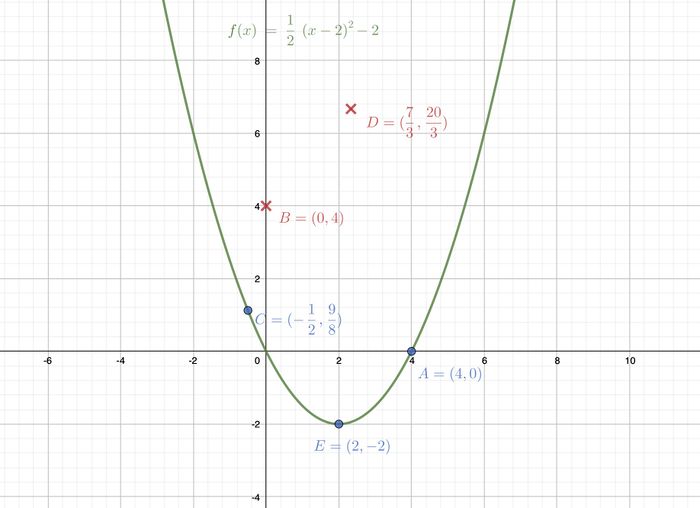
<math>E=(2,-2)</math>. | <math>E=(2,-2)</math>. | ||
a) Überprüfe rechnerisch, ob die Punkte A, B, C, D und E auf dem Graphen von f liegen.<br /><br /> | '''a)''' Überprüfe rechnerisch, ob die Punkte A, B, C, D und E auf dem Graphen von f liegen.<br /><br /> | ||
b) Zeichne den Graphen der Funktion f und die Punkte A-E in dein Heft. Vergleiche anschließend die Ergebnisse aus a) mit deiner Zeichnung<br> | '''b)''' Zeichne den Graphen der Funktion f und die Punkte A-E in dein Heft. Vergleiche anschließend die Ergebnisse aus a) mit deiner Zeichnung<br> | ||
Version vom 19. Mai 2019, 11:41 Uhr
Scheitelpunktform
Wir schauen uns die Funktion an. Funktionen dieser Art heißen qua dra tisch e Funktionen. Der Graph einer solchen Funktion ist eine Pa ra bel. Der höchste bzw. der tiefste Punkt eines solchen Funktionsgraphen heißt Schei tel punkt. Liegt die Funktionsgleichung in der Scheitelpunktform vor, wie es hier der Fall ist, dann kann der Scheitelpunkt S direkt aus der Funktionsgleichung abgelesen werden. Der Parameter d ist die x-Koordinate und der Parameter e ist die y-Koordinate des Scheitelpunkts. S(d,e).
Ist der Parameter a kleiner als Null (a<0), dann ist der Graph der Funktion g nach un ten geöffnet.
Ist a größer als Null (a>0), dann ist der Graph von g nach o ben geöffnet.
Ist a größer als Eins (a>1) oder kleiner als minus Eins (a<-1), dann sieht der Graph von g schma ler aus. Man sagt, dass in diesem Fall der Graph ge streckt wird.
Liegt a zwischen minus Eins und Eins (-1<a<1), dann sieht der Graph von g brei ter aus. Man sagt, dass in diesem Fall der Graph ge staucht wird.
Ist d größer als Null (d>0), dann wird der Graph von g nach rechts verschoben.
Ist d kleiner als Null (d<0), dann wird der Graph von g nach links verschoben.
Ist e kleiner als Null (e<0), dann wird der Graph von g nach un ten verschoben.
Ist e größer als Null (e>0), dann wird der Graph von g nach o ben verschoben.
Umwandlung Scheitelpunktform und Normalenform