Benutzer:Buss-Haskert/Trigonometrie/Sinusfunktion: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 96: | Zeile 96: | ||
auf die Graphen der Funktionen | auf die Graphen der Funktionen | ||
:f(x) = | :f(x) = a·sin x | ||
</div> | </div> | ||
| Zeile 108: | Zeile 108: | ||
auf die Graphen der Funktionen | auf die Graphen der Funktionen | ||
: f(x) = sin ( b | :f(x) = sin ( b · x ) | ||
| Zeile 120: | Zeile 120: | ||
auf die Graphen der Funktionen | auf die Graphen der Funktionen | ||
: f(x) = sin ( x + c ) | :f(x) = sin ( x + c ) | ||
| Zeile 132: | Zeile 132: | ||
auf die Graphen der Funktionen | auf die Graphen der Funktionen | ||
: | : f(x) = sin x + d | ||
| Zeile 141: | Zeile 141: | ||
Alternativ kannst du den Lernpfad weiter durcharbeiten, dort sind jeweils die Applets gegeben und die Beobachtungen in den Lösungen notiert. | Alternativ kannst du den Lernpfad weiter durcharbeiten, dort sind jeweils die Applets gegeben und die Beobachtungen in den Lösungen notiert. | ||
====Die Bedeutung des Parameters a in | ====Die Bedeutung des Parameters a in f(x) = a·sin x ==== | ||
Wir betrachten nun den Einfluss von <math> a </math> in | Wir betrachten nun den Einfluss von <math> a </math> in | ||
:<math> x \rightarrow a\cdot \sin x </math>. | :<math> x \rightarrow a\cdot \sin x </math>. | ||
{{Box|1= | {{Box|1=Die Bedeutung von a in f(x) = a · sin x|2= | ||
<ggb_applet height="450" width="900" id="yye6hqbw" /> <br> | <ggb_applet height="450" width="900" id="yye6hqbw" /> <br> | ||
# Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von <math> a </math> ändern. <br> | # Öffne dieses GeoGebra-Applet. Mit dem Schieberegler kannst du den Wert von <math> a </math> ändern. <br> | ||
| Zeile 164: | Zeile 164: | ||
}} | }} | ||
====Die Bedeutung der Parameters b in | ====Die Bedeutung der Parameters b in f(x) = sin ( b · x ) ==== | ||
Wir betrachten nun den Einfluss von <math> b </math> in | Wir betrachten nun den Einfluss von <math> b </math> in | ||
| Zeile 170: | Zeile 170: | ||
{{Box|1= | {{Box|1=Der Parameter b in f(x) = sin (b·x)|2= | ||
<ggb_applet height="450" width="900" id="e7wkrhyj" /> <br> | <ggb_applet height="450" width="900" id="e7wkrhyj" /> <br> | ||
| Zeile 192: | Zeile 192: | ||
}} | }} | ||
====Die Bedeutung des Parameters c in | ====Die Bedeutung des Parameters c in f(x) = sin ( x + c ) ==== | ||
Wir betrachten nun den Einfluss von <math> c </math> in | Wir betrachten nun den Einfluss von <math> c </math> in | ||
:<math> x \rightarrow \sin ( x + c ) </math>. | :<math> x \rightarrow \sin ( x + c ) </math>. | ||
{{Box|1= | {{Box|1=Der Parameter c in f(x) = sin (x + c)|2= | ||
<ggb_applet height="450" width="900" id="ypthxjcu" /> <br> | <ggb_applet height="450" width="900" id="ypthxjcu" /> <br> | ||
| Zeile 216: | Zeile 216: | ||
}} | }} | ||
====Die Bedeutung des Parameters d in | ====Die Bedeutung des Parameters d in f(x) = sin x + d ==== | ||
Wir betrachten nun den Einfluss von <math> d </math> in | Wir betrachten nun den Einfluss von <math> d </math> in | ||
:<math> x \rightarrow \sin x + d </math>. | :<math> x \rightarrow \sin x + d </math>. | ||
{{Box|1= | {{Box|1=Der Parameter d in f(x) = sin x + d|2= | ||
<ggb_applet height="450" width="900" id="jr7hupnz" /> <br> | <ggb_applet height="450" width="900" id="jr7hupnz" /> <br> | ||
| Zeile 246: | Zeile 246: | ||
{{Box|1= | {{Box|1= Zusatz 1|2= | ||
Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von diesem [http://www.gymnasium-walldorf.de/mathematik/trigo_otto/trigo.html Applet] und betrachte sie! Was fällt dir auf? | Welcher Zusammenhang besteht zwischen der Sinus- und der Kosinusfunktion? Zeichne dazu die Graphen der Funktionen <math>\,\!x \rightarrow \sin\left(x+\frac{\pi}{2}\right)</math> und <math>\,\!x \rightarrow \cos(x)</math> in dein Heft oder mit Hilfe von diesem [http://www.gymnasium-walldorf.de/mathematik/trigo_otto/trigo.html Applet] und betrachte sie! Was fällt dir auf? | ||
{{Lösung versteckt|Überlege dir zunächst die Lage der Nullstellen und die Größe der Amplitude!|Tipp zum Zeichnen ins Heft|Tipp ausblenden}} | {{Lösung versteckt|Überlege dir zunächst die Lage der Nullstellen und die Größe der Amplitude!|Tipp zum Zeichnen ins Heft|Tipp ausblenden}} | ||
| Zeile 257: | Zeile 257: | ||
<span style="background-color:yellow;"> Man erhält den Graphen der Kosinusfunktion, indem man z.B. den Graphen der Sinusfunktion um <math>\frac{\pi}{2}</math> nach links verschiebt. | <span style="background-color:yellow;"> Man erhält den Graphen der Kosinusfunktion, indem man z.B. den Graphen der Sinusfunktion um <math>\frac{\pi}{2}</math> nach links verschiebt. | ||
Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion.|3=Merksatz}} | Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion.|3=Merksatz}} | ||
|2=Lösung zu | |2=Lösung zu Zusatz 1|3=Ausblenden}} | ||
| Zeile 274: | Zeile 274: | ||
{{Box|1= | {{Box|1=Zusatz 2|2= | ||
Bringe den Smily zum Lachen! Variiere dazu die verschiedenen Parameter der allgemeinen Sinusfunktion und beobachte die Auswirkungen auf den Graphen. | Bringe den Smily zum Lachen! Variiere dazu die verschiedenen Parameter der allgemeinen Sinusfunktion und beobachte die Auswirkungen auf den Graphen. | ||
| Zeile 280: | Zeile 280: | ||
<ggb_applet width="690" height="517" version="4.2" id="dtyeqjsn" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> <br> | <ggb_applet width="690" height="517" version="4.2" id="dtyeqjsn" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> <br> | ||
</center>|3=Arbeitsmethode}} | </center>|3=Arbeitsmethode}} | ||
Version vom 5. April 2023, 14:40 Uhr
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3) Berechnungen in allgemeinen Dreiecken
4) Berechnungen in beliebigen Figuren
5 Sinusfunktion und Kosinusfunktion
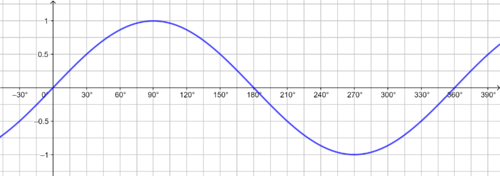
Die Zuordnung der Sinuswerte zu einem Winkel ist eindeutig, d.h. es handelt sich um eine Funktion, die Sinusfunktion.
Auf dieser Seite lernst du die verschiedenen Darstellungen (Text, Wertetabelle, Gleichung und Graph) zur Sinusfunktion kennen. Auch die Sinusfunktion enthält die Parameter a, b, c und d und du erforscht deren Bedeutung.
Erinnerst du dich an die Bedeutung der Parameter m und b bei den linearen Funktionen f(x) = mx + b bzw. an die Bedeutung von a, d und e bei den quadratischen Funktionen f(x) = a(x + d)² + e?
Ebenso erforscht du die Sinusfunktion.
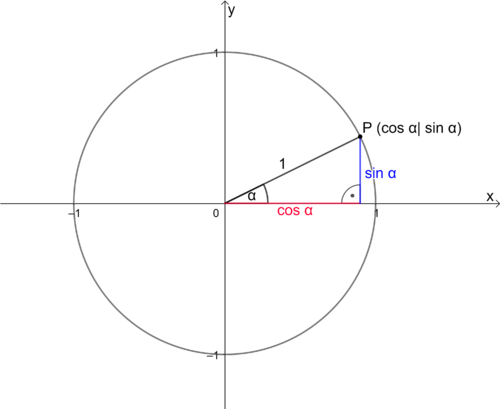
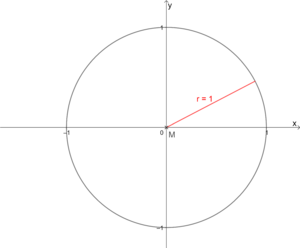
5.1 Der Einheitskreis
Der Einheitskreis ist ein besonderer Kreis: Sein Mittelpunkt liegt im Ursprung M(0|0) und sein Radius beträgt r = 1 LE (Längeneinheit).
Auf den Kreisrand liegen also alle Punkte, die vom Ursprung den Abstand 1 haben.
Am Einheitskreis lassen sich die Streckenverhältnisse Sinus, Kosinus und Tangens gut verdeutlichen:
Originallink https://www.geogebra.org/m/p2hcjn3f

Applet von Buß-Haskert
5.2 Sinusfunktion und Kosinusfunktion

Applet von Reinhard Schmidt Originallink https://www.geogebra.org/m/tjt2hhs2
Stellst du dir den Punkt P des Einheitskreises als eine Gondel an einem Riesenrad vor und trägst die Höhe der Gondel zu einem bestimmten Zeitpunkt dar, ergibt sich der Graph der Sinusfunktion.

Applet nach Matthias Heinitz Originallink https://www.geogebra.org/m/drb6q4ry

Applet von Buß-Haskert (nach chje) Originallink: https://www.geogebra.org/m/stgatxum
5.3 Die allgemeinen Sinusfunktion: Bedeutung der Parameter für den Verlauf des Graphen
Dieses Kapitel orientiert sich am Lernpfad "Trigonometrische Funktionen" von Silvia Joachim, Karl Haberl und Franz Embacher. Er wurde erstellt unter der Lizenz CC BY SA (https://unterrichten.zum.de/wiki/Trigonometrische_Funktionen/Einfluss_der_Parameter). Herzlichen Dank!
Untersuche den Einfluss von
auf die Graphen der Funktionen
- f(x) = a·sin x
Untersuche den Einfluss von
auf die Graphen der Funktionen
- f(x) = sin ( b · x )
Untersuche den Einfluss von
auf die Graphen der Funktionen
- f(x) = sin ( x + c )
Untersuche den Einfluss von
auf die Graphen der Funktionen
- f(x) = sin x + d
Alternativ kannst du den Lernpfad weiter durcharbeiten, dort sind jeweils die Applets gegeben und die Beobachtungen in den Lösungen notiert.
Die Bedeutung des Parameters a in f(x) = a·sin x
Wir betrachten nun den Einfluss von in
- .
Die Bedeutung der Parameters b in f(x) = sin ( b · x )
Wir betrachten nun den Einfluss von in
- .
Die Bedeutung des Parameters c in f(x) = sin ( x + c )
Wir betrachten nun den Einfluss von in
- .
Die Bedeutung des Parameters d in f(x) = sin x + d
Wir betrachten nun den Einfluss von in
- .
Jetzt noch was zum Knobeln!!!
Ja genau, die Graphen der beiden angegebenen Funktionen sind identisch. Genauer gesagt:
Du hast eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen herausgefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.