Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Gleichungen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 68: | Zeile 68: | ||
===1.3 Quadratische Gleichungen lösen=== | ===1.3 Quadratische Gleichungen lösen=== | ||
{{#ev:youtube|ypYxTOgDetQ|800|center}} | {{#ev:youtube|ypYxTOgDetQ|800|center}} | ||
====1.3.1) Rein quadratische Gleichungen lösen==== | |||
{{Box|1=Rein quadratische Gleichungen|2=Eine quadratische Gleichung heißt rein quadratisch, wenn die Variable ausschließlich in der zweiten Potenz vorkommt:<br> | |||
'''ax² = c'''|3=Arbeitsmethode}} | |||
{{Box|Übung: Rein quadratische Gleichungen lösen|Löse die nachfolgende App.|Üben}} | |||
{{LearningApp|app=p88cbqzo320|width=100%|heigth=300px}} | |||
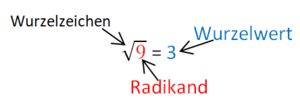
{{Box|1=Anzahl der Lösungen quadratischer Gleichungen|2=Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel):<br> | |||
Die Gleichung hat <span style="color:red">zwei</span> Lösungen, <span style="color:green">eine</span> oder <span style="color:blue">keine</span> Lösung, wenn der Radikand <span style="color:red">positiv</span>, <span style="color:green">null</span> oder <span style="color:blue">negativ</span> ist.|3=Arbeitsmethode}} | |||
{{Lösung versteckt|[[Datei:Begriff Radikand.png|rahmenlos]]|Begriff Radikand|Verbergen}} | |||
====1.3.2) Gemischt quadratische Gleichungen lösen==== | |||
Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.<br> | |||
===== Lösen durch Ausklammern: Gleichungen der Form x² + bx = 0 ===== | |||
Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.<br> | |||
Beginnen wir mit dem besonderen Fall, dass die Gleichung die Form x² + bx = 0 hat, es also keinen Term "ohne" Variable gibt und eine Seite den Wert 0 hat. | |||
{{Box|1=Gemischt quadratische Gleichungen lösen durch Ausklammern|2=Hat die Gleichung die Form '''x² + bx = 0''', so kannst du '''x ausklammern''':<br> | |||
x² + bx = 0 <br> | |||
x(x + b) = 0 Dieses Produkt wird nur 0, wenn einer der beiden Faktoren 0 ist (Satz vom Nullprodukt), also<br> | |||
x = 0 oder x + b = 0 |-b<br> | |||
x<sub>1</sub> = 0 oder x<sub>2</sub> = -b.|3=Arbeitsmethode}} | |||
{{LearningApp|app=pt87u3ef520|width=100%|heigth=600px}}<br> | |||
=====Lösen durch quadratische Ergänzung: Gleichungen der Form x² + bx + c = 0===== | |||
{{Box|1=Gemischt quadratische Gleichungen lösen durch quadratische Ergänzung|2=Hat die Gleichung die Form x² + bx + c = 0, löst du die Gleichung mithilfe der quadratischen Ergänzung:<br> | |||
Stelle die Gleichung um: x² + bx = -c.<br> Mithilfe der quadratischen Ergänzung <math>\left ( \frac{b}{2} \right )^2</math> auf beiden Seiten der Gleichung, wird dann der Term x² + bx zu einem Binom umgeformt. Dann wird auf beiden Seiten der Gleichung die Wurzel gezogen.|3=Arbeitsmethode}} | |||
Schau das Video zur Beispielaufgabe an. Schreibe das Beispiel in dein Heft und mache dir Notizen zu jedem Schritt der Lösung. | |||
{{#ev:youtube|Ok73gEoo1j4|800|center}} | |||
<br> | |||
{{LearningApp|app=pcse2ekgt20|width=100%|height=600px}} | |||
{{LearningApp|app=pcse2ekgt20|width=100%|height=600px}} | |||
=====Lösen mit der Lösungsformel: p-q-Formel===== | |||
Mit der quadratischen Ergänzung kannst du gemischt quadratische Gleichungen lösen. Eine weitere Möglichkeit ist die Anwendung der Lösungsformel: Die p-q-Formel.<br> | |||
Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten '''Normalform''' gegeben sein:<br> | |||
'''x² + px + q = 0'''<br> | |||
{{Lösung versteckt|1=Die Struktur muss also so sein, dass die Zahl 1 der Koeffizient von x² ist (also "nichts" vor x² steht, die 1 können wir uns denken) und die andere Seite der Gleichung 0 ist. Dann ist p der Koeffizient von x (also die Zahl vor x) und q ist die Zahl ohne Variable.|2=Was muss ich für die Normalform beachten?|3=Verbergen}} | |||
{{Box|1=Lösen mit der Lösungsformel: p-q-Formel|2=Jede quadratische Gleichung lässt sich mit der p-q-Formel lösen. Dazu muss die Gleichung zunächst in die Normalform x² + px + q = 0 umgeformt werden. Dann werden die Werte für p und q bestimmt und in die Formel eingesetzt:<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}</math><br> | |||
Achte dabei auf die Vorzeichen von p und q.|3=Arbeitsmethode}} | |||
<br> | |||
Präge dir die Lösungsformel ein mit dem Lied von Dorfuchs. Höre es so oft, bis es ein Ohrwurm wird: | |||
{{#ev:youtube|tRblwTsX6hQ|800|center}} | |||
<br> | |||
Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q. | |||
{{LearningApp|app=p887tapq520|width=100%|heiht=600px}} | |||
<br> | |||
Löse die nächsten Aufgaben mit der Lösungsformel. Schreibe wie im Beispiel: | |||
x² - 22x + 72 = 0 |Setze ein: p=-22; <math>\tfrac{p}{2}</math>=-11; -<math>\tfrac{p}{2}</math>=11; q=72 <br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{11^2-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{121-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{49}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm</math>7<br> | |||
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br> | |||
Kurzschreibweise:<br> | |||
x² - 22x + 72 = 0 |Setze ein: p=-22; <math>\tfrac{p}{2}</math>=-11; -<math>\tfrac{p}{2}</math>=11; q=72 <br> | |||
x<sub>1/2</sub> = 11<math>\pm\sqrt{11^2-72}</math><br> | |||
x<sub>1/2</sub> = 11<math>\pm</math>7<br> | |||
x<sub>1</sub> = 18; x<sub>2</sub> = 4<br> | |||
{{LearningApp|app=p5430i34t20|width=100%|height=600px}}<br> | |||
{{LearningApp|app=p53v9bz7220|width=100%|height=600px}}<br> | |||
=====Allgemein quadratische Gleichungen lösen===== | |||
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.<br> | |||
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a. | |||
Ordne in der nachfolgenden LearningApp, ob es sich um die Normalform oder die allgemeine Form quadratischer Gleichungen handelt. | |||
{{LearningApp|app=pb85ajz4k20|width=100%|height=400px}} | |||
Jede quadratische Gleichung lässt sich in die Normalform x² + px + q = 0 umformen. Dann können wir wieder die p-q-Formel zur Lösung anwenden. | |||
{{Box|1=Allgemein quadratische Gleichungen lösen|2=Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0. <br>Alle quadratischen Gleichungen lassen sich umformen in die Normalform x² + px + q = 0. Dann kann wieder die p-q-Formel zur Lösung angewendet werden.<br> | |||
1. Schritt: Forme in die Normalform x² + px + q = 0 um.<br> | |||
2. Schritt: Wende die p-q-Formel x<sub>1/2</sub> = -<math>\tfrac{p}{2}\pm\sqrt{\left ( \frac{p}{2} \right )^2-q}</math> an.|3=Arbeitsmethode}} | |||
Übe zunächst das Umwandeln in die Normalform: | |||
{{LearningApp|app=p5ut2b9xc20|width=100%|height=400px}} | |||
Ein Video zur Zusammenfassung: | |||
{{#ev:youtube|UXYYntGcyY4|600|center}} | |||
{{Box|1=Anzahl der Lösungen quadratischer Gleichungen|2=Die Anzahl der Lösungen quadratischer Gleichungen hängt vom Radikand ab(vom Wert unter der Wurzel). Der Radikand <math>\left ( \frac{p}{2} \right )^2-q</math> wird '''Diskriminante D''' genannt.<br>Die Anzahl der Lösungen ist abhängig von D.<br> | |||
Die Gleichung hat <span style="color:red">zwei</span> Lösungen, <span style="color:green">eine</span> oder <span style="color:blue">keine</span> Lösung, wenn die Diskriminante D <span style="color:red">positiv</span>, <span style="color:green">null</span> oder <span style="color:blue">negativ</span> ist.|3=Arbeitsmethode}} | |||
Beispiele:<br> | |||
<div class="grid"> | |||
<div class="width-1-3">'''D > 0''', <span style="color:red">zwei</span> Lösungen:<br> | |||
1. x² + 6x + 5 = 0 |<math>\tfrac{p}{2} = 3; q = 5</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{3^2-5}</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{4}</math> D = 4 (positiv)<br> | |||
x<sub>1/2</sub> = -3<math>\pm</math>2 | |||
x<sub>1</sub> = -1 ; x<sub>2</sub> = -5<br> | |||
</div> | |||
<div class="width-1-3">'''D = 0''',<span style="color:green">eine</span> Lösung:<br> | |||
2. x² + 6x + 9 = 0 |<math>\tfrac{p}{2} = 3; q = 9</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{3^2-9}</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{0}</math> D = 0 <br> | |||
x<sub>1/2</sub> = -3<math>\pm</math>0 | |||
</div> | |||
<div class="width-1-3"> '''D < 0''',<span style="color:blue">keine</span> Lösung:<br> | |||
3. x² + 6x + 10 = 0 |<math>\tfrac{p}{2} = 3; q = 10</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{3^2-10}</math><br> | |||
x<sub>1/2</sub> = -3<math>\pm\sqrt{-1}</math> D < 0 (negativ)<br> | |||
<math>\sqrt{-1}</math> ist nicht lösbar, da das Quadrat einer Zahl niemals negativ ist, also die Wurzel nie aus einer negativen Zahl gezogen werden kann.</div> | |||
</div> | |||
{{LearningApp|app=2626415|width=100%|height=600px}} | |||
{{Box|Übung 11: Vermischte Übungen|Wähle Aufgaben auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/quadratischeGleichung.shtml '''Aufgabenfuchs'''] Nr. 1 - 19 .|Üben}} | |||
{{Box|Übung: Quadratische Gleichungen lösen|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch. | {{Box|Übung: Quadratische Gleichungen lösen|Löse die Aufgaben aus dem Buch. Vergleiche deine Lösungen mit denen hinten im Buch. | ||
* S. 121, P34 - P37|Üben}} | * S. 121, P34 - P37|Üben}} | ||
Version vom 29. Dezember 2022, 12:10 Uhr
SEITE IM AUFBAU!!
Gleichungen lösen
1.1 Lineare Gleichungen lösen
1.2 Lineare Gleichungssysteme (LGS)
1.3 Quadratische Gleichungen lösen
1.3.1) Rein quadratische Gleichungen lösen
1.3.2) Gemischt quadratische Gleichungen lösen
Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.
Lösen durch Ausklammern: Gleichungen der Form x² + bx = 0
Eine Gleichung heißt "gemischt quadratisch", wenn die Variable in der zweiten Potenz (z.B. x²) und in einfacher Potenz (z.B. x) vorkommt.
Beginnen wir mit dem besonderen Fall, dass die Gleichung die Form x² + bx = 0 hat, es also keinen Term "ohne" Variable gibt und eine Seite den Wert 0 hat.
Lösen durch quadratische Ergänzung: Gleichungen der Form x² + bx + c = 0
Schau das Video zur Beispielaufgabe an. Schreibe das Beispiel in dein Heft und mache dir Notizen zu jedem Schritt der Lösung.
Lösen mit der Lösungsformel: p-q-Formel
Mit der quadratischen Ergänzung kannst du gemischt quadratische Gleichungen lösen. Eine weitere Möglichkeit ist die Anwendung der Lösungsformel: Die p-q-Formel.
Damit diese Formel angewendet werden darf, muss die gemischt quadratische Gleichung in der sogenannten Normalform gegeben sein:
x² + px + q = 0
Präge dir die Lösungsformel ein mit dem Lied von Dorfuchs. Höre es so oft, bis es ein Ohrwurm wird:
Übe zunächst das Umstellen der Gleichung ein die Normalform und die Bestimmung von p und q.
Löse die nächsten Aufgaben mit der Lösungsformel. Schreibe wie im Beispiel:
x² - 22x + 72 = 0 |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 11
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4
Kurzschreibweise:
x² - 22x + 72 = 0 |Setze ein: p=-22; =-11; -=11; q=72
x1/2 = 11
x1/2 = 117
x1 = 18; x2 = 4
Allgemein quadratische Gleichungen lösen
Allgemein quadratische Gleichungen sind Gleichungen in der Form ax² + bx + c = 0.
Im Unterschied zur Normalform ist hier der Koeffizient von x² eine beliebige Zahl a.
Ordne in der nachfolgenden LearningApp, ob es sich um die Normalform oder die allgemeine Form quadratischer Gleichungen handelt.
Jede quadratische Gleichung lässt sich in die Normalform x² + px + q = 0 umformen. Dann können wir wieder die p-q-Formel zur Lösung anwenden.
Übe zunächst das Umwandeln in die Normalform:
Ein Video zur Zusammenfassung:
Beispiele:
1. x² + 6x + 5 = 0 |
x1/2 = -3
x1/2 = -3 D = 4 (positiv)
x1/2 = -32
x1 = -1 ; x2 = -5
2. x² + 6x + 9 = 0 |
x1/2 = -3
x1/2 = -3 D = 0
x1/2 = -30
3. x² + 6x + 10 = 0 |
x1/2 = -3
x1/2 = -3 D < 0 (negativ)