Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden kennenlernen: Unterschied zwischen den Versionen
(Aufgabe 6) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 73: | Zeile 73: | ||
==Besondere Pyramiden?== | ==Besondere Pyramiden?== | ||
{{Box|1=Aufgabe 6: Ecken, Kanten und Flächen|2=Wir haben bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen. Wechsle für die nächste Aufgabe zu deinem Arbeitsblatt und bearbeite Aufgabe 6: Ecken, Kanten und Flächen. | <nowiki>{{Box|1=Aufgabe 6: Ecken, Kanten und Flächen|2=Wir haben bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen. Wechsle für die nächste Aufgabe zu deinem Arbeitsblatt und bearbeite Aufgabe 6: Ecken, Kanten und Flächen.</nowiki> | ||
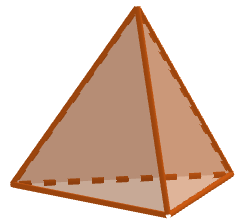
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Dreieck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei:Dreieck zuschnitt.png|mini|Pyramide mit Dreieck als Grundfläche]] |2=Tipp zu a)|3=Tipp zu a)}} | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Dreieck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei:Dreieck zuschnitt.png|mini|Pyramide mit Dreieck als Grundfläche]] |2=Tipp zu a)|3=Tipp zu a)}} | ||
| Zeile 87: | Zeile 87: | ||
Die Pyramide hat eine Grundfläche und 4 Seitenflächen. Insgesamt hat die Pyramide somit '''5 Flächen'''.|2=Lösung zu b)|3=Lösung zu b)}} | Die Pyramide hat eine Grundfläche und 4 Seitenflächen. Insgesamt hat die Pyramide somit '''5 Flächen'''.|2=Lösung zu b)|3=Lösung zu b)}} | ||
{{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Sechseck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei: | {{Lösung versteckt|1=Hier siehst du eine Pyramide mit einem Sechseck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung. [[Datei:Pyramide mit Sechseck als Grundfläche.png|mini|Pyramide mit Sechseck als Grundfläche]]|2=Tipp zu c)|3=Tipp zu c)}} | ||
{{Lösung versteckt|1=Die Grundfläche der Pyramide hat 6 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''7 Ecken'''. | {{Lösung versteckt|1=Die Grundfläche der Pyramide hat 6 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit '''7 Ecken'''. | ||
Die Grundfläche der Pyramide hat 6 Kanten. Dazu kommen 6 Seitenkanten, also insgesamt '''12 Kanten'''. | Die Grundfläche der Pyramide hat 6 Kanten. Dazu kommen 6 Seitenkanten, also insgesamt '''12 Kanten'''. | ||
Version vom 19. November 2022, 13:05 Uhr
Körper
Als Start in die Welt der Pyramiden wiederholen wir noch einmal ein paar andere Körper, die du schon aus dem Mathematikunterricht kennst.
Pyramiden im Alltag
Jetzt konzentrieren wir uns aber auf unser heutiges Thema, die Pyramiden. Zum Start überlegen wir, wo Pyramiden in unserem Alltag auftauchen können.
Pyramide oder keine Pyramide?
Nun haben wir schon einen ersten Eindruck gewonnen, wie Pyramiden in der echten Welt aussehen können.Im folgenden Schritt wollen wir uns mathematischen Besonderheiten des Körpers Pyramide nähern.
Wie sieht eine Pyramide aus?
Wir wollen uns nun Pyramiden genauer anschauen und die wichtigsten Begriffe erlernen.
Im nächsten Schritt erarbeiten wir die Definition einer Pyramide.
Besondere Pyramiden?
{{Box|1=Aufgabe 6: Ecken, Kanten und Flächen|2=Wir haben bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen. Wechsle für die nächste Aufgabe zu deinem Arbeitsblatt und bearbeite Aufgabe 6: Ecken, Kanten und Flächen.
Die Grundfläche der Pyramide hat 3 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 4 Ecken. Die Grundfläche der Pyramide hat 3 Kanten. Dazu kommen 3 Seitenkanten, also insgesamt 6 Kanten.
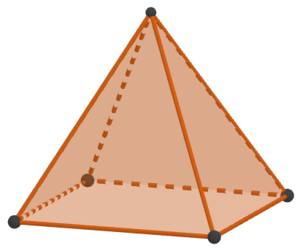
Die Pyramide hat eine Grundfläche und 3 Seitenflächen. Insgesamt hat die Pyramide also 4 Flächen.Hier siehst du eine Pyramide mit einem Viereck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
Die Grundfläche der Pyramide hat 4 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 5 Ecken. Die Grundfläche der Pyramide hat 4 Kanten. Dazu kommen 4 Seitenkanten, also hat die Pyramide insgesamt 8 Kanten.
Die Pyramide hat eine Grundfläche und 4 Seitenflächen. Insgesamt hat die Pyramide somit 5 Flächen.Die Grundfläche der Pyramide hat 6 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 7 Ecken. Die Grundfläche der Pyramide hat 6 Kanten. Dazu kommen 6 Seitenkanten, also insgesamt 12 Kanten.
Die Pyramide hat eine Grundfläche und 6 Seitenflächen. Insgesamt hat die Pyramide also 7 Flächen.
Nun solltest du Pyramiden von anderen Körpern unterscheiden und diese genauer charakterisieren können. Falls du das Gefühl haben solltest, dass dir dies noch schwer fällt, wiederhole das Kapitel gerne, bis du dich sicherer fühlst. Wenn du schon ein Pyramiden-Profi bist, kannst du zum nächsten Kapitel wechseln!