Buss-Haskert/Gleichungen (mit Klammern)/Anwendungsaufgaben

zurück zur Seite der Herta-Lebenstein-Realschule

Gleichungen (mit Klammern) Startseite
1) Gleichungen mit Klammern
2) Anwendungsaufgaben
3) Formeln
4) Checkliste

Anwendungsaufgaben zu Gleichungen mit Klammern

Es gibt verschiedene Bereiche, in denen Gleichungen mit Klammern Anwendung finden:

Bist du fit? Vorübungen

Vorübung 1: Mathematische Texte

Um Zahlenrätsel lösen zu können, musst du die Fachbegriffe kennen. Übe dies im nachfolgenden Quiz

Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten

Addition	addieren	vermehren	plus
Subtraktion	subtrahieren	vermindern	minus
Multiplikation	multiplizieren	verdoppeln	vervielfachen	mal
Division	dividieren	halbieren	teilen	geteilt

Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme.

Vorübung 2: Geometrische Anwendungen

Anwendungsaufgaben aus dem Bereich Geometrie erfordern Kenntnisse über verschiedene Figuren. Löse das nachfolgende Quiz zur Wiederholung.

Quadrat		u = 4·a	A = a²
Rechteck		u = 2a + 2b	A = a·b
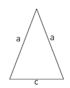
gleichschenkliges Dreieck		u = 2a + c	2 gleich lange Seiten	α+β+γ=180°
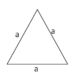
gleichseitiges Dreieck		u = 3a	3 gleich lange Seiten	α+β+γ=180°

Vorübung 3: Sachsituationen

Ordne in der nachfolgen den Termen die passende Bedeutung zu.

In allen Anwendungsbereichen ist es wichtig, dass du den Text genau liest, dir die Situation vorstellst und mit eigenen Worten beschreibst.

6-Schritte-Verfahren für Anwendungsaufgaben

6-Schritte-Verfahren

Eine Hilfe zur Lösung von Anwendungsaufgaben ist das 6-Schritte-Verfahren. Übertrage die Beispielaufgabe in dein Heft. Notiere auch die Bemerkungen zu den Schritten.

Diese 6 Schritte helfen dir beim Lösen der Anwendungsaufgaben. Beachte vor allem die Schritte 1 und 2. Notiere genau, welche Bedeutung die Variable hat und stelle die Terme passend zum Text auf. Dann schaffst es es sicherlich auch, eine Gleichung aufzustellen und diese zu lösen.

Mathematische Texte

Bei mathematischen Texten ist die Variable immer die gesuchte Zahl. Gehe schrittweise vor (6-Schritte-Verfahren).

Übung 1: Mathematische Texte

Ordne in den LearningApps den mathematischen Texten die passenden Gleichungen zu.

Übung 2: Mathematische Texte

Löse die Aufgaben aus dem Buch. Wende das 6-Schritte-Verfahren an.

• S. 34 Nr. 9
• S. 39 Nr. 11

Lösungen (bunt gemischt) 3; 10; 16; 25. Denke an einen Antwortsatz: Die gesuchte Zahl ist ___.

Hinweis: Beim Subtrahieren steht die Zahl, von der etwas abgezogen wird, vorne.
Ein Term lautet also 51-5x.
Schreibe das Divisionszeichen als Bruchstrich, dann ist der Term übersichtlicher.
Der zweite Term heißt also $\frac{2x}{3}$.

Löse die Gleichung nun auf, indem du als erstes mit dem Nenner 3 multiplizierst.
51 - 5x = $\frac{2x}{3}$ |·3 Multipliziere jeden Summanden mit 3!
153 - 15x = 2x

...

Sprinteraufgaben zu mathematischen Texten

• Löse einige Aufgaben von Nr. 39-58 Aufgabenfuchs.
• Löse einige Aufgaben: Text in eine Gleichung übersetzen.

Notiere die Lösung in deinem Heft.

Geometrische Anwendungen

Bei geometrischen Anwendungen zeichne immer eine Skizze! Sie hilft dir, die Bedeutung der Variablen festzulegen und die Terme passend aufzustellen.

Übung 3: Geometrische Anwendungen

Wende in den LearningApps das 6-Schritte-Verfahren an. Denke an eine Skizze!

Übung 4: Geometrische Anwendungen

Löse die Aufgaben aus dem Buch. Wende das 6-Schritte-Verfahren an. Denke an eine Skizze!

• S. 27 Nr. 8
• S. 34 Nr. 3
• S. 34 Nr. 4
• S. 34 Nr. 5
• S. 34 Nr. 6.

Der Flächeninhalt eines Rechtecks: A = Länge · Breite oder A = a·b.

Flächeninhalt rotes Rechteck: A = 9·(x+4)
Flächeninhalt schwarzes Rechteck: A = 15·x
Wenn die Rechtecke flächengleich sind, muss also gelten

9(x+4) = 15x
Löse diese Gleichung nach x auf.

rotes Rechteck: Länge x+2; Breite x
schwarzes Rechteck: Länge x+2-5 = x-3 Breite x+8.
Gleichung: (x+2)x = (x-3)(x+8) Klammern auflösen:"Jeder gibt jedem die Hand"

Winkelsumme im Dreieck: α + β+ γ = 180°
Vielleicht hilft es dir, α=x zu nennen, dann kannst du die Variable x in der Gleichung verwenden (statt α)

Gleichung:α + β+ γ = 180° also
α + (α + 15°) + (α + 30°)= 180°
bzw. mit der Variabel x

x + (x + 15) + (x + 30) = 180   |"Plusklammer auflösen"

Wähle z.B. γ=x
Dann sind die Terme für α und β
α=2x
β=3x

Es gilt wieder, dass die Winkelsumme 180° beträgt. Stelle die Gleichung auf.

x Breite des Recktecks
x+8 Länge des Rechtecks
u = 84cm Erinnerung: Umfang ist drum herum ("Kalle läuft").

Bestimme zunächst x mithilfe der Flächeninhalte. Diese sind gleich groß. Stelle eine passende Gleichung auf und löse sie nach x auf. Lösung: x=6

Bestimme nun die jeweiligen Seitenlängen, indem du für x den Wert 6 einsetzt und berechne dann den Umfang.

(Lösung: A 46m; B 38m

Sprinteraufgaben zu geometrischen Anwendungen

• Löse einige Aufgaben von Nr. 59-64 Aufgabenfuchs.
• Löse einige Aufgaben: Flächen von Rechtecke vergleichen.

Notiere die Lösung in deinem Heft.

Sachsituationen

Übung 5: Altersaufgaben

Wende in den LearningApps das 6-Schritte-Verfahren an. Es handelt sich hier um Aufgaben rund um das Alter.

Übung 6: Altersaufgaben

Löse die Aufgaben aus dem Buch. Wende das 6-Schritte-Verfahren an.

• S. 33 das Beispiel
• S. 34 Nr. 8
• S. 34 Nr. 11

Es wir von drei Personen gesprochen: von Erna, Lisa und Karin. Da Erna doppelt so alt ist wie Karin, empfiehlt es sich, die Bedeutung der Variablen mit
x = Alter von Karin
festzulegen. Stelle damit die Terme für das Alter von Erna und Lisa auf.

Bedeutung der Variblen: Alter von Karin = x
Terme aufstellen: Alter von Erna = 2x

                             Alter von Lisa = 2x-50

Das Alter der Band-Mitglieder bezieht sich oft auf das von Mike. Wähle x=Alter von Mike. Stelle dann im zweiten Schritt die Terme für das Alter der anderen Bandmitglieder auf. (Natürlich kannst du auch das Alter eines anderen Bandmitgliedes als x festlegen, probiere es aus.)

Übung 7: Sachsituationen

Löse die Aufgaben aus dem Buch. Wende das 6-Schritte-Verfahren an.

• S. 34 Nr. 7
• S. 34 Nr. 10
• S. 39 Nr. 13.

gesucht: Wie viele Kisten können die beiden Personen mit in den Aufzug nehmen?
Entnimm die entsprechenden Werte dem Bild. (Lösung x=20)

Bedeutung der Variablen: x zurückgelegte Strecke am ersten Tag
Stelle nun Terme für die übrigen Tage auf.
(Lösung x=52)

Es sind 4 Geschwister. Wähle x=Betrag des jüngsten Kindes. Dann erhält das nächst ältere Kind x+600, das darauf folgende x+600+600 usw.

Übung 8: Sachsituationen

Erfinde selbst eine Anwendungsaufgabe und löse sie. Erstelle dann dazu eine LearningApp (Lückentext) unter deinem Schüleraccount. Deine Lehrerin wird diese prüfen und dann in den Klassenordner hochladen.

Wenn du Schwierigkeiten bei der Erstellung der App hast, schicke ein Bild deiner Aufgabe an deine Lehrerin.

Sprinteraufgaben zu Sachsituationen

Löse einige Aufgaben von Nr. 65-81 Aufgabenfuchs. Notiere die Lösung in deinem Heft.

Test 2

Bist du fit?

Hast du alle Hefteinträge abgeschrieben und alle Aufgaben gelöst? Dann bearbeite den Test 2. Du erhältst ihn von deiner Lehrerin.
Bearbeite den Test allein. Kontrolliere dein Ergebnis mit der Musterlösung.

Wie viele Punkte hast du erreicht? Wähle den passenden Link unten aus.

0-15 Punkte: Bearbeite weitere Aufgaben auf der Seite Aufgabenfuchs ab Nr. 39 passend zu deinen Fehlerschwerpunkten. Aufgabenfuchs

16-24 Punkte: 3) Formeln

3) Formeln