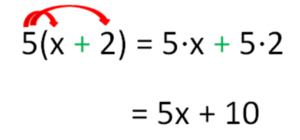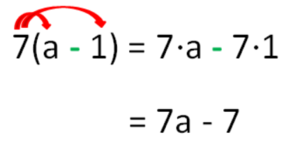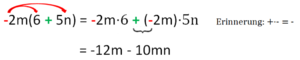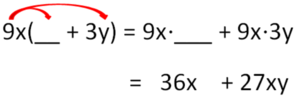Benutzer:Buss-Haskert/Terme(mit Klammern): Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 113: | Zeile 113: | ||
{{Box|Übung 2|Bearbeite die Aufgabe aus dem Buch. | {{Box|Übung 2|Bearbeite die Aufgabe aus dem Buch. | ||
* S. 11 Nr. 1 |Üben}} | * S. 11 Nr. 1 |Üben}} | ||
{{Lösung versteckt|Um die Gesamtfläche als Summe auszudrücken, addiere die Flächeninhalte der einzelnen kleinen Rechtecke. Um die Gesamtfläche als Produkt auszudrücken, bestimme die gesamten Seitenlängen und berechne den Flächeninhalt mit "Länge ⋅ Breite".|Tipp 1 zu Nr. 1|Verbergen}} | |||
{{Lösung versteckt|Um die Gesamtfläche als Summe auszudrücken, addiere die Flächeninhalte der einzelnen kleinen Rechtecke. Um die Gesamtfläche als Produkt auszudrücken, bestimme die gesamten Seitenlängen und berechne den Flächeninhalt mit "Länge ⋅ Breite".|Tipp 1 zu Nr. 1|Verbergen}} | |||
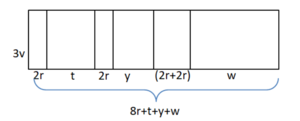
{{Lösung versteckt|Summe: Die Figur lässt sich in drei Teilrechtecke zerlegen, mit jeweils der Breite x und den verschiedenen Längen r, s und t. Die Gesamtfläche setzt sich zusammen aus der Summe von x⋅r + x⋅s + x⋅t. | {{Lösung versteckt|Summe: Die Figur lässt sich in drei Teilrechtecke zerlegen, mit jeweils der Breite x und den verschiedenen Längen r, s und t. Die Gesamtfläche setzt sich zusammen aus der Summe von x⋅r + x⋅s + x⋅t. | ||
Produkt: Die Figur ist ein Rechteck mit der Breite x und der Länge (r + s + t), die Gesamtflächen berechnen wir mit "Länge⋅Breite", also (r + s + t)⋅x [oder x⋅(r + s + t)].|Tipp 2 zu Nr. 1b|Verbergen}} | Produkt: Die Figur ist ein Rechteck mit der Breite x und der Länge (r + s + t), die Gesamtflächen berechnen wir mit "Länge⋅Breite", also (r + s + t)⋅x [oder x⋅(r + s + t)].|Tipp 2 zu Nr. 1b|Verbergen}} | ||
{{Box|Übung 3|Löse die Aufgabe aus dem Buch, eine Skizze kann dir helfen. Info: Der Buchstabe M steht für "Mantelfläche". So wird die Summe der Seitenflächen eines Quaders bezeichnet. | {{Box|Übung 3|Löse die Aufgabe aus dem Buch, eine Skizze kann dir helfen. Info: Der Buchstabe M steht für "Mantelfläche". So wird die Summe der Seitenflächen eines Quaders bezeichnet. | ||
* S. 12 Nr. 13a,b und d. |Üben}} | * S. 12 Nr. 13a,b und d. |Üben}} | ||
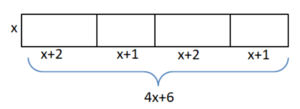
{{Lösung versteckt|1=Skizze zu a)[[Datei:Mantel a.png|mini]] | |||
Summe: M = x⋅(x+2) + x⋅(x+1) + x⋅(x+2) + x⋅(x+1)<br> | Summe: M = x⋅(x+2) + x⋅(x+1) + x⋅(x+2) + x⋅(x+1)<br> | ||
Produkt: M = x⋅(4x+6)|2=Tipp zu Nr. 13a)|3=Verbergen}} | Produkt: M = x⋅(4x+6)|2=Tipp zu Nr. 13a)|3=Verbergen}} | ||
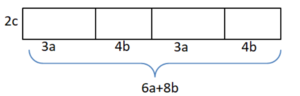
{{Lösung versteckt|Skizze zu b) [[Datei:Mantel b.png|mini]]|Tipp zu Nr. 13b)|Verbergen}} | |||
{{Lösung versteckt|Skizze zu b) [[Datei:Mantel b.png|mini]]|Tipp zu Nr. 13b)|Verbergen}} | {{Lösung versteckt|Skizze zu d) [[Datei:Mantel d.png|mini]]|Tipp zu Nr. 13d)|Verbergen}} | ||
{{Box|Übung 4|Erstelle selbst eine LearningApp, in der die Gesamtfläche als Summe und als Produkt ausgedrückt werden kann.|Üben}} | {{Box|Übung 4|Erstelle selbst eine LearningApp, in der die Gesamtfläche als Summe und als Produkt ausgedrückt werden kann.|Üben}} | ||
| Zeile 177: | Zeile 171: | ||
* S. 12, Nr. 11<br> | * S. 12, Nr. 11<br> | ||
|Üben}} | |Üben}} | ||
{{Lösung versteckt|Die Malpunkte zwischen der Zahl bzw. der Variablen und der Klammer wurden teilweise weggelassen, du musst sie im Kopf ergänzen. Hier also: 5(x+ 2) ist dasselbe wie 5⋅(x+2)|Tipp 1 zu Nr. 2|Verbergen}} | |||
{{Lösung versteckt|Die Malpunkte zwischen der Zahl bzw. der Variablen und der Klammer wurden teilweise weggelassen, du musst sie im Kopf ergänzen. Hier also: 5(x+ 2) ist dasselbe wie 5⋅(x+2)|Tipp 1 zu Nr. 2|Verbergen}} | {{Lösung versteckt|Ausmultiplizieren: Jedem die Hand geben! Notiere als Hilfe Bögen über die Zahlen bzw. Variablen, die du multiplizierst.[[Datei:Ausmultiplizieren Bsp 1a.png|mini]]|Tipp 2 zu Nr. 2a|Verbergen}} | ||
{{Lösung versteckt|Vorsicht mit den Vorzeichen und Rechenzeichen: Das Zeichen in der Klammer wird übernommen und mit der Zahl vor der Klammer multipliziert[[Datei:Ausmultiplizieren Bsp 2.png|mini]]|Tipp 3 zu Nr. 2c|Verbergen}} | |||
{{Lösung versteckt|Ausmultiplizieren: Jedem die Hand geben! Notiere als Hilfe Bögen über die Zahlen bzw. Variablen, die du multiplizierst.[[Datei:Ausmultiplizieren Bsp 1a.png|mini]]|Tipp 2 zu Nr. 2a|Verbergen}} | {{Lösung versteckt|Vorsicht mit den Vorzeichen und Rechenzeichen: Hat der Term außerhalb der Klammer ein Minuszeichen, wird dies mit multipliziert[[Datei:Ausmultiplizieren Bsp 3a.png|mini]]|Tipp 4 zu Nr. 2d|Verbergen}} | ||
{{Lösung versteckt|1=Welcher Term muss jeweils ergänzt werden, damit beim Ausmultiplizieren die vorgegebene Lösung entsteht? In Aufgabe a) ist es die "4", denn 9x(4+3y) = 36x + 27xy[[Datei:Ausmultiplizieren Bsp 4.png|mini]]|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Lösung versteckt|Vorsicht mit den Vorzeichen und Rechenzeichen: Das Zeichen in der Klammer wird übernommen und mit der Zahl vor der Klammer multipliziert[[Datei:Ausmultiplizieren Bsp 2.png|mini]]|Tipp 3 zu Nr. 2c|Verbergen}} | {{Lösung versteckt|Das Distributivgesetz gilt auch für die Division (Nr. 10) und für mehrere Summanden (Nr. 11)|Tipp zu Nr. 10 und 11|Verbergen}} | ||
{{Lösung versteckt|Vorsicht mit den Vorzeichen und Rechenzeichen: Hat der Term außerhalb der Klammer ein Minuszeichen, wird dies mit multipliziert[[Datei:Ausmultiplizieren Bsp 3a.png|mini]]|Tipp 4 zu Nr. 2d|Verbergen}} | |||
{{Lösung versteckt|1=Welcher Term muss jeweils ergänzt werden, damit beim Ausmultiplizieren die vorgegebene Lösung entsteht? In Aufgabe a) ist es die "4", denn 9x(4+3y) = 36x + 27xy[[Datei:Ausmultiplizieren Bsp 4.png|mini]]|2=Tipp zu Nr. 5|3=Verbergen}} | |||
{{Lösung versteckt|Das Distributivgesetz gilt auch für die Division (Nr. 10) und für mehrere Summanden (Nr. 11)|Tipp zu Nr. 10 und 11|Verbergen}} | |||
{{Box|Zusätzliche Übungen zum Ausmultiplizieren (bei Bedarf)|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-vereinfachen.shtml '''Aufgabenfuchs'''] die Aufgaben | {{Box|Zusätzliche Übungen zum Ausmultiplizieren (bei Bedarf)|Löse auf der Seite [https://mathe.aufgabenfuchs.de/gleichung/terme-vereinfachen.shtml '''Aufgabenfuchs'''] die Aufgaben | ||
* 22 | * 22 | ||
Version vom 17. Juni 2022, 13:58 Uhr
Damit du dem Lernpfad folgen kannst, prüfe zunächst dein Vorwissen mithilfe der Aufgaben in der nachfolgenden Tabelle.
Zusätzliche Aufgaben findest du in deinem Account bei ANTON.
2. Summen multiplizieren
3. Binomische Formeln und 4. Faktorisieren mit binomische Formeln
5. Zusammenfassung
6. Checkliste
Vorwissen
Bearbeite die Aufgaben in der Tabelle: (Buch: Schnittpunkt Mathematik - Differenzierende Ausgabe 8, Klett)
| Du kannst | Übungen im Buch | Übungen online |
|---|---|---|
| mit Fachbegriffen umgehen | S. 8 Nr. 1 |
|
| -Terme aufstellen und benennen | S. 8 Nr. 2 |
|
| -Terme addieren und subtrahieren | S.8 Nr. 3 |
|
| -Terme multiplizieren und dividieren | S.8 Nr. 4 (+Kahoot!) |
|
| -Terme mit Klammern vereinfachen
(+ 🙂und - ↯) |
S.8 Nr. 5 |
|
| - Werte von Termen berechnen | S. 8 Nr. 7 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
1. Ausmultiplizieren und Ausklammern (• vor der Klammer )
Vergleiche deine Ideen mit denen im nachfolgenden Video:
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.

Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.

Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:
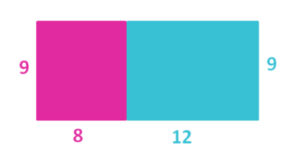
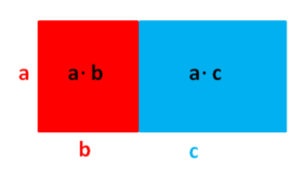
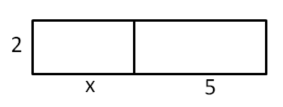
Auch hier ist das große Rechteck aus den kleinen Flächen zusammengesetzt. Der Flächeninhalt kann auf zwei Arten angegeben werden:
als Produkt der Seitenlängen a ⋅ ⟨b+c⟩ und als Summe der einzelnen Flächen a⋅b + a⋅c
Es gilt also: a⋅(b+c) = a⋅b + a⋅c.
Summe: Die Figur lässt sich in drei Teilrechtecke zerlegen, mit jeweils der Breite x und den verschiedenen Längen r, s und t. Die Gesamtfläche setzt sich zusammen aus der Summe von x⋅r + x⋅s + x⋅t.
Produkt: Die Figur ist ein Rechteck mit der Breite x und der Länge (r + s + t), die Gesamtflächen berechnen wir mit "Länge⋅Breite", also (r + s + t)⋅x [oder x⋅(r + s + t)].
1.1 Ausmultiplizieren
Durch Ausmultiplizieren wird ein Produkt in eine Summe umgewandelt, die Klammern werden also aufgelöst.
Beispiele:
1.2 Ausklammern
Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt.
Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.
Hier sind die Faktoren, die ausgeklammert werden müssen, angegeben.
a) 8⋅(...) b) 7x⋅(...) c) 11y⋅(...) d) 9b(-...+...) e) 20s(...) f) 15vw(...)