Benutzer:L.hodankov/Wurzeln/Übungen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
(Aufgaben ausgetauscht)
Markierung: 2017-Quelltext-Bearbeitung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 46: Zeile 46:




===4.2 Irrationale Zahlen - Bestimmen von Quadratwurzeln===
===4.2* Irrationale Zahlen - Bestimmen von Quadratwurzeln===


Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.<br>
Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.<br>
Zeile 53: Zeile 53:
<math>\sqrt{2}</math> hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.<br><br>
<math>\sqrt{2}</math> hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.<br><br>
{{Box|Irrationale Zahlen|Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.|Arbeitsmethode}}<br><br>
{{Box|Irrationale Zahlen|Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.|Arbeitsmethode}}<br><br>
Den meisten ist es zwar egal, doch <math>\sqrt{2}</math> ist irrational...
 
{{#ev:youtube|tPfnEByx9r0|800|center}}<br>
{{Box|1=Nährerungsweises Bestimmen von Quadratwurzeln|2=Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:<br>
{{Box|1=Nährerungsweises Bestimmen von Quadratwurzeln|2=Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:<br>
<math>\sqrt{30}</math> liegt zwischen den Zahlen 5 und 6, denn<br>
<math>\sqrt{30}</math> liegt zwischen den Zahlen 5 und 6, denn<br>
5² < 30 < 6²|3=Arbeitsmethode}}
5² < 30 < 6²|3=Arbeitsmethode}}
{{Box | Übung 3 - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
{{Box | Übung 3(*) - online|Löse auf der Seite [https://mathe.aufgabenfuchs.de/potenz/wurzel.shtml '''Aufgabenfuchs''']
*  Nr. 21|Üben}}<br><br>
*  Nr. 21|Üben}}<br><br>


Zeile 80: Zeile 79:
* Nr. 34
* Nr. 34
* Nr. 35|Üben}}
* Nr. 35|Üben}}
{{Box|1=n-te Wurzel|2=Die n-te Wurzel einer Zahl a ist die Zahl b, die n-mal mit sich selbst malgenommen die Zahl a ergibt: b<math>\cdot</math>b<math>\cdot ... \cdot</math>b = a, also gilt <math>\sqrt[n]{a}</math>=b.<br>|3=Arbeitsmethode}}

Version vom 9. Dezember 2021, 20:27 Uhr

Diese Seite des Lernpfades wurde teilweise übernommen von der Seite Herta-Lebenstein-Realschule https://projekte.zum.de/wiki/Benutzer:Buss-Haskert/Potenzen. Der Autor ist Buss-Haskert. Diese Seite wurde veröffentlicht unter der Lizenz CC BY SA.

Herzlichen Dank!

Seite im Aufbau!

SEITE IM AUFBAU!!


4 Wurzeln/Quadratwurzeln - Definition

Definition Einstieg.png

4.1 (Quadrat)wurzel - Definition

(Quadrat)wurzel - Definition
Rabbit-pulling-carrot-2256824 1280.png
Die Quadratwurzel aus einer positiven Zahl b ist die positive Zahl a, die mit sich selbst multipliziert b ergibt:

a² = b und
a =

Fachbegriffe:
Begriff Radikand.png


Teste dich:


Wiederholung Quadratzahlen:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400

25² = 625
Übung 1 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • Nr. 2 - 11



Jetzt bist du fit für weitere Aufgaben:

Übung 2

Löse die Aufgaben bei Learningapps.


Übung 3

Löse die Aufgaben vom AB 24 "Wurzelziehen: Übungen".


4.2* Irrationale Zahlen - Bestimmen von Quadratwurzeln

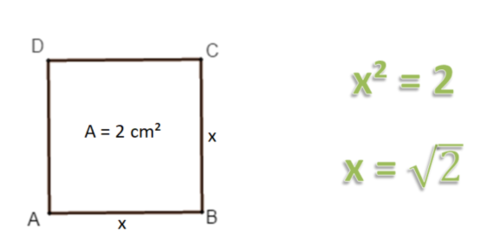
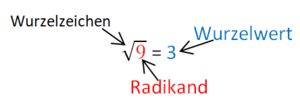
Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.
So liegt z.B. der Wert von im Intervall [1;2], also zwischen und 1 und 2, denn 1² < 2 < 2².
Dieses Intervall kannst du verkleinern, um den Wert von auf mehrere Nachkommastellen anzunähern.

hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.

Irrationale Zahlen
Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen haben, die nicht periodisch werden. Quadratwurzeln aus Zahlen, die keine Quadratzahlen sind, sind irrational.




Nährerungsweises Bestimmen von Quadratwurzeln

Du kannst durch Annäherung feststellen, zwischen welchen natürlichen Zahlen die Quadratwurzel einer Zahl liegt:
liegt zwischen den Zahlen 5 und 6, denn

5² < 30 < 6²
Übung 3(*) - online

Löse auf der Seite Aufgabenfuchs

  • Nr. 21




4.3 Kubikwurzeln - 3. Wurzel und n-te Wurzel

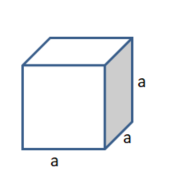
Wenn du die Kantenlänge eines Würfels mit einem Volumen von 8cm³ bestimmen möchtest, muss du die Zahl finden, die dreimal mit sich selbst multipliziert 8 ergibt:
222 = 23 = 8, die Kubikwurzel ist dann wie folgt definiert:
=2
Die 3. Wurzel aus 8 ist 2. Die 3. Wurzel heißt auch Kubikwurzel (von engl. "cube" = Würfel).


Kubikwurzel - 3. Wurzel
Die 3. Wurzel einer Zahl a ist die Zahl b, die dreimal mit sich selbst malgenommen die Zahl a ergibt: bbb = a, also gilt =b.


Übung 4 - online

Löse auf der Seite Aufgabenfuchs

  • Nr. 30
  • Nr. 31
  • Nr. 32
  • Nr. 33
  • Nr. 34
  • Nr. 35


n-te Wurzel
Die n-te Wurzel einer Zahl a ist die Zahl b, die n-mal mit sich selbst malgenommen die Zahl a ergibt: bbb = a, also gilt =b.
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:L.hodankov/Wurzeln/Übungen&oldid=57643“