Digitale Werkzeuge in der Schule/Mathematik trifft Kunst/Kunstwerke analysieren – Achsensymmetrie erkennen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 44: | Zeile 44: | ||
<br> | <br> | ||
{{Box | Aufgabe 3: Richtig oder Falsch?!| | {{Box | Aufgabe 3: Richtig oder Falsch?!| | ||
Anna hat die Aufgaben 1 und 2 auch bearbeitet und sich folgendes dazu notiert. '''Beurteile''' ob ihre Aussagen richtig oder falsch sind | Anna hat die Aufgaben 1 und 2 auch bearbeitet und sich folgendes dazu notiert. '''Beurteile''' ob ihre Aussagen richtig oder falsch sind, indem du das entsprechende Kästchen anklickst. | ||
<quiz display="simple"> | <quiz display="simple"> | ||
Version vom 21. November 2021, 19:53 Uhr
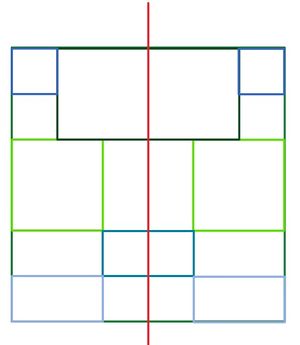
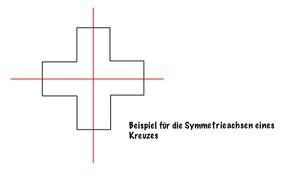
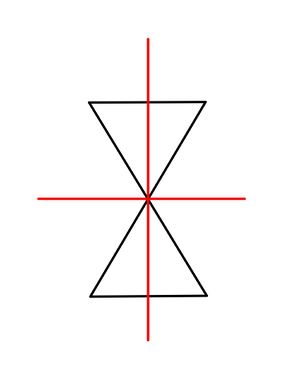
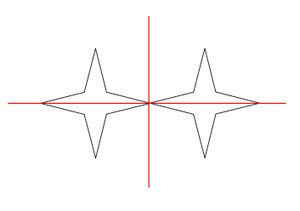
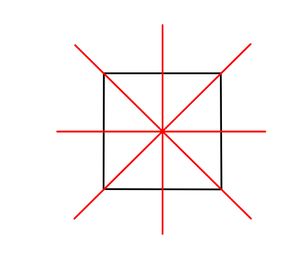
Eigenschaften gespiegelter Kunstwerke entdecken
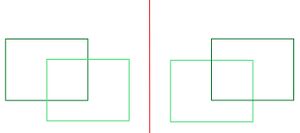
Achsensymmetrisch oder nicht?
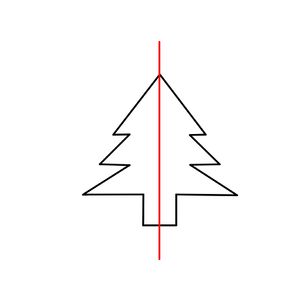
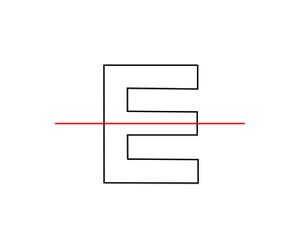
Symmetrieachse finden
Zusätzliche Eigenschaften von achsensymmetrischen Figuren