Benutzer:Buss-Haskert/Quadratische Funktionen/Verschiebung entlang der y-Achse: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (Tipp berichtigt) Markierung: Quelltext-Bearbeitung 2017 |
(Bilder ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 34: | Zeile 34: | ||
{{Lösung versteckt|1="Punktprobe"!<br> | {{Lösung versteckt|1="Punktprobe"!<br> | ||
Setze die Koordinaten der Punkte in die Funktionsgleichungen ein und prüfe, ob eine wahre (w) Aussage oder falsche (f) Aussage entsteht. Demnach liegt der Punkt auf der Parabel bzw. nicht auf der Parabel.|2=Tipp zu Nr. 14|3=Verbergen}} | Setze die Koordinaten der Punkte in die Funktionsgleichungen ein und prüfe, ob eine wahre (w) Aussage oder falsche (f) Aussage entsteht. Demnach liegt der Punkt auf der Parabel bzw. nicht auf der Parabel.|2=Tipp zu Nr. 14|3=Verbergen}} | ||
{{Lösung versteckt|1=Tipp zu Nr. 16 (Bilderfolge zur Nutzung von GeoGebra)|2= | {{Lösung versteckt|1=Tipp zu Nr. 16 (Bilderfolge zur Nutzung von GeoGebra)|2=[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 1.png|rahmenlos]]<br> | ||
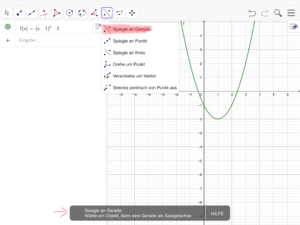
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 2.png|rahmenlos]]<br> | |||
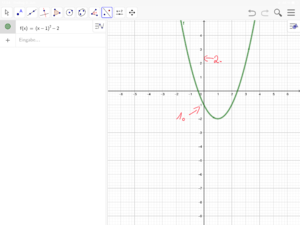
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 3.png|rahmenlos]]<br> | |||
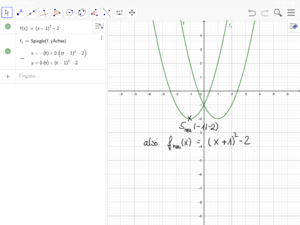
[[Datei:Verschobene Normalparabel spiegeln (GeoGebra) 4.png|rahmenlos]]|3=Verbergen}} | |||
{{Fortsetzung|weiter=5 Scheitelpunktform quadratischer Funktionen|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform}} | {{Fortsetzung|weiter=5 Scheitelpunktform quadratischer Funktionen|weiterlink=Benutzer:Buss-Haskert/Quadratische Funktionen/Scheitelpunktform}} | ||
Version vom 28. August 2021, 09:33 Uhr
SEITE IM AUFBAU
Quadratische Funktionen - Startseite
1 Quadratische Funktionen entdecken
2 Die Normalparabel f(x) = x²
3 Die gestreckte und gestauchte Parabel: Bedeutung des Parameters a in f(x) = ax²
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
5 Die Scheitelpunktform quadratischer Funktionen
4 Die verschobene Parabel: Bedeutung des Parameters c in f(x) = ax² + c
Link zu GeoGebra
Falls du die Schieberegler nicht erstellen kannst, nutze das nachfolgende Applet.

"Punktprobe"!
<div class="loesung-verstecken mw-collapsible mw-collapsed" data-expandtext="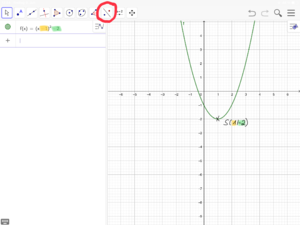
 " data-collapsetext="Verbergen">
" data-collapsetext="Verbergen">
Tipp zu Nr. 16 (Bilderfolge zur Nutzung von GeoGebra)



