Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 230: | Zeile 230: | ||
{{Lösung versteckt|1= Eine Parametergleichung für die Ebene lautet: <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math>|2=Lösung zu a) anzeigen |3=Lösung verbergen}} | {{Lösung versteckt|1= Eine Parametergleichung für die Ebene lautet: <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math>|2=Lösung zu a) anzeigen |3=Lösung verbergen}} | ||
{{Lösung versteckt|1= <math>| | {{Lösung versteckt|1= <math>|\begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}\| = 2</math>; <math> |\begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}| = \sqrt{8}</math> | ||
Für die Parameter gilt: <math>0 \le r \le 4{,}5</math> und <math>0 \le s \le \frac{7}{\sqrt{8}}</math> | Für die Parameter gilt: <math>0 \le r \le 4{,}5</math> und <math>0 \le s \le \frac{7}{\sqrt{8}}</math> | ||
| Zeile 236: | Zeile 236: | ||
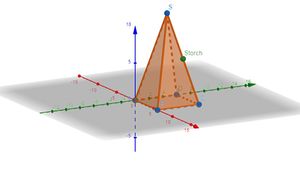
Die Punkte der Dachfläche können beschrieben werden durch die Parameterdarstellung <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix} ; 0 \le r \le 4{,}5 ; 0 \le s \le \frac{7}{\sqrt{8}}</math>|2=Lösung zu b) anzeigen |3=Lösung verbergen}} | Die Punkte der Dachfläche können beschrieben werden durch die Parameterdarstellung <math>E: \vec{x} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+r \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+s\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix} ; 0 \le r \le 4{,}5 ; 0 \le s \le \frac{7}{\sqrt{8}}</math>|2=Lösung zu b) anzeigen |3=Lösung verbergen}} | ||
{{Lösung versteckt|1= <math>\vec{OB} = \begin{pmatrix} 0 \\ 9 \\ 4 | {{Lösung versteckt|1= <math>\vec{OB} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+0 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+\frac{7}{\sqrt{8}}\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>B ({-}4{,}95|9|8{,}95)</math> | ||
<math>\vec{OC} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix} + 4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 | <math>\vec{OC} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+\frac{7}{\sqrt{8}}\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>C ({-}4{,}95|0|8{,}95)</math> | ||
<math>\vec{OD} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix} + 4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 | <math>\vec{OD} = \begin{pmatrix} 0 \\ 9 \\ 4 \end{pmatrix}+4{,}5 \cdot \begin{pmatrix} 0 \\ {-}2 \\ 0 \end{pmatrix}+0\cdot \begin{pmatrix} {-}2 \\ 0 \\ 2 \end{pmatrix}</math> also <math>D (0|0|4)</math> | ||
Punkte, die außerhalb der Dachfläche liegen: | Punkte, die außerhalb der Dachfläche liegen: | ||
z.B.: | z.B.: | ||
<math>r=5, s=4 </math> <math>P_1({-}8|{-}1|12)</math> | <math>r=5, s=4 </math> <math>P_1({-}8|{-}1|12)</math> | ||
<math>r={-}1, s={-}1</math> <math>P_2(2|11|2)</math> | <math>r={-}1, s={-}1</math> <math>P_2(2|11|2)</math> | ||
<math>r={-}1, s=0 </math> <math>P_3(0|11|4)</math>|2=Lösung zu c) anzeigen |3=Lösung verbergen}}| Arbeitsmethode }} | <math>r={-}1, s=0 </math> <math>P_3(0|11|4)</math>|2=Lösung zu c) anzeigen |3=Lösung verbergen}}| Arbeitsmethode }} | ||
Version vom 18. Juni 2021, 19:21 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
Geradlinig begrenzte Flächen
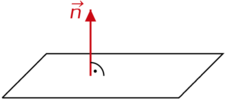
⭐ Normalenvektor
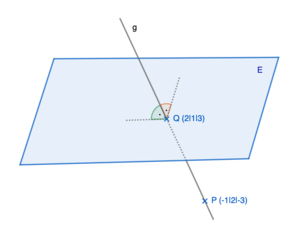
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform
⭐Arbeiten mit den unterschiedlichen Ebenengleichungen