Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 380: | Zeile 380: | ||
<br />{{Box | Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung | | <br />{{Box | Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung | | ||
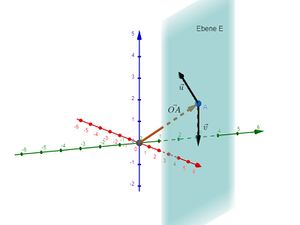
Wir suchen die Koordinatengleichung der Ebene <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>. | Wir suchen die Koordinatengleichung der Ebene <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}</math>. | ||
| Zeile 397: | Zeile 398: | ||
\Leftrightarrow & & n_1 &= n_2 & &\mid :(-24)\\ | \Leftrightarrow & & n_1 &= n_2 & &\mid :(-24)\\ | ||
\end{align}</math></div> | \end{align}</math></div> | ||
Durch Einsetzen der berechneten, von n_1 abhängigen Werte in die zweite Gleichung erhalten wir auch n_3 und damit den allgemeinen Normalenvektor in Abhängigkeit von <math>n_1</math>: | |||
<div align="center"><math> \vec{n} = \begin{pmatrix} n_1 \\ n_1 \\ \tfrac{1}{2} n_1 \end{pmatrix} </math></div> | |||
Für einen speziellen Normalenvektor wählen wir für <math>n_1</math> eine beliebige Zahl aus. Die wählen wir so, dass insgesamt ganzzahlige Zahlen raus kommen. Wenn <math>n_1 = 2</math> ist, dann folgt für <math>n_2 = 2</math> und für <math>n_3 = 1</math>. | |||
Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} </math> | Daraus folgt für den speziellen Normalenvektor <math> \vec{n} = \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} </math> | ||
| Zeile 404: | Zeile 411: | ||
Um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}</math> mit <math>\vec{OA}=\begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix}</math> und erhält <math>d=11</math>. | Um <math>d</math> zu bestimmen, berechnet man das Skalarprodukt von <math>\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}</math> mit <math>\vec{OA}=\begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix}</math> und erhält <math>d=11</math>. | ||
Die Koordinatengleichung lautet somit: <math>E\colon 2x_1+2x_2+x_3=11</math>|Hervorhebung1}} | Die Koordinatengleichung lautet somit: <math>E\colon 2x_1+2x_2+x_3=11</math>| Hervorhebung1}} | ||
Version vom 6. Juni 2021, 21:03 Uhr
Die Parameterform und die Punktprobe
Die Punktprobe
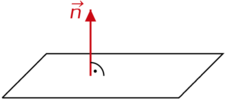
⭐ Normalenvektor
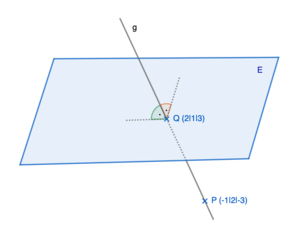
⭐ Normalenform und Koordinatenform von Ebenengleichungen
⭐Überführung der Parameterform in die Koordinatenform