Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2.3 Wertetabelle und Funktionsgleichung: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 26: | Zeile 26: | ||
===Punktprobe: Liegt der Punkt auf der Geraden?=== | ===Punktprobe: Liegt der Punkt auf der Geraden?=== | ||
{{Box|Lineare Funktionen erkennen - Bootsverleih| [[Datei:Boat-307125 1280.png|rechts|rahmenlos|200x200px]]Aufgabe 1: Tom und Lisa möchten im Urlaub ein Tretboot ausleihen. Die Grundgebühr beträgt 5€, pro Stunde zahlen sie 2€ Miete.<br> | |||
Sie leihen für 3 Stunden ein Tretboot. Der Bootsverleiher rechnet den Preis 10€ aus. Kann das sein? | |||
|Meinung}} | |||
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt. | Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt. | ||
geg: Punkt A(3|10); Funktion f(x) = 2x + 5 | geg: Punkt A(3|10); Funktion f(x) = 2x + 5 | ||
| Zeile 85: | Zeile 86: | ||
<br> | <br> | ||
===Fehlende Koordinate eines Punktes der Funktion berechnen=== | ===Fehlende Koordinate eines Punktes der Funktion berechnen=== | ||
{{Box|Lineare Funktionen erkennen - Bootsverleih| [[Datei:Boat-307125 1280.png|rechts|rahmenlos|200x200px]]Aufgabe 1: Tom und Lisa möchten im Urlaub ein Tretboot ausleihen. Die Grundgebühr beträgt 5€, pro Stunde zahlen sie 2€ Miete.<br> | |||
Tom und Lisa leihen ein Tretboot für 1,5 Stunden. Wie viel müssen sie bezahlen? | |||
|Meinung}} | |||
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen. | Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen. | ||
| Zeile 90: | Zeile 94: | ||
'''1. Möglichkeit: <span style="color:red">x</span>-Koordinate ist gegeben'''<br> | '''1. Möglichkeit: <span style="color:red">x</span>-Koordinate ist gegeben'''<br> | ||
geg: <span style="color:red">x = 1,5</span> und f(x) = 2x+5 | geg: <span style="color:red">x = 1,5</span> und f(x) = 2x+5 | ||
| Zeile 172: | Zeile 175: | ||
===Schnittpunkte mit den Koordinatenachsen bestimmen=== | ===Schnittpunkte mit den Koordinatenachsen bestimmen=== | ||
{{Box|Lineare Funktionen erkennen - Pool|[[Datei:Smartphone-2953932 1280.png|rechts|rahmenlos|200x200px]] Aufgabe 3: Der Pool des Hotels muss geleert werden. Zu Beginn steht das Wasser 2 m hoch. Der Wasserstand sinkt stündlich um 10 cm. | |||
Nach welcher Zeit ist der Pool leer?|Meinung}} | |||
{{#ev:youtube|KnOdPP4gqmc}} | {{#ev:youtube|KnOdPP4gqmc}} | ||
| Zeile 178: | Zeile 182: | ||
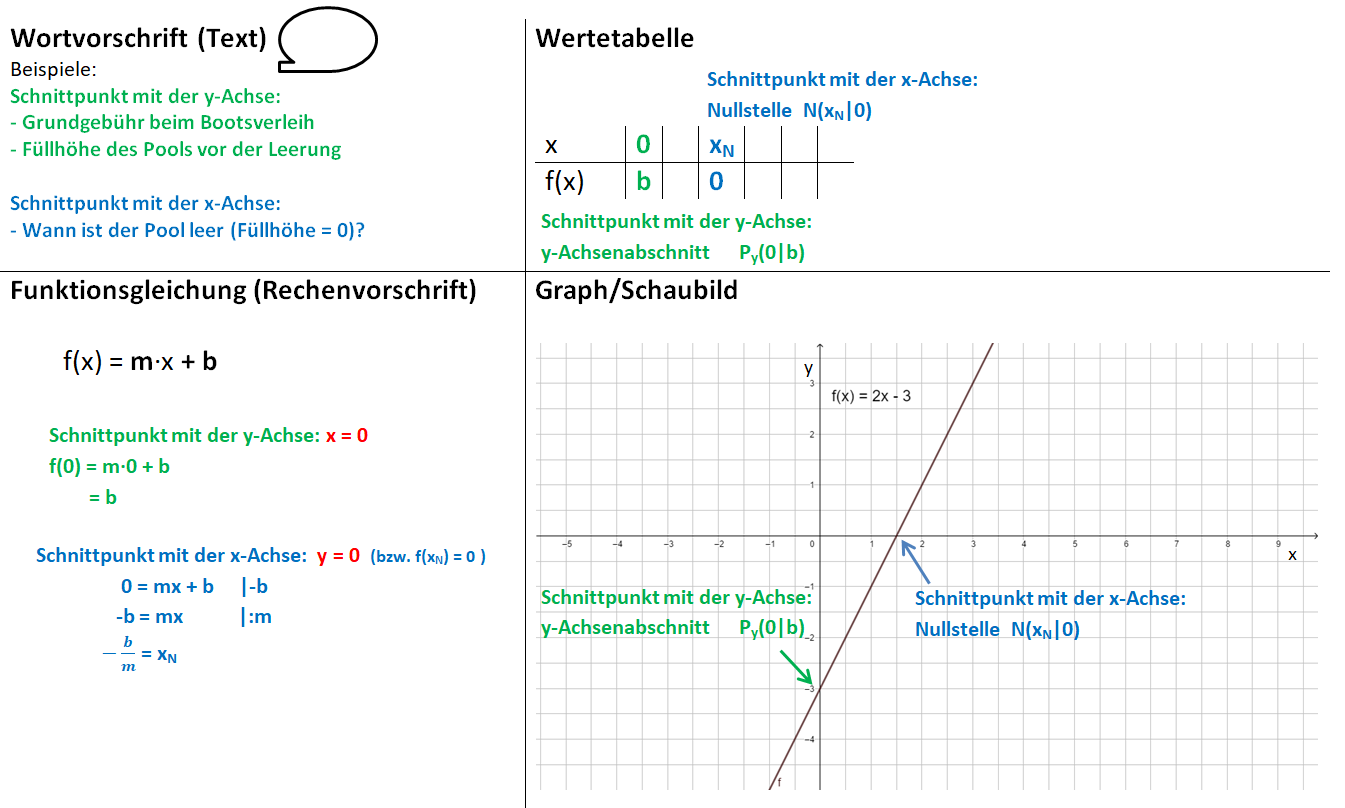
{{Box|1=Schnittpunkte mit den Koordinatenachsen|2=Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. | {{Box|1=Schnittpunkte mit den Koordinatenachsen|2=Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. | ||
P<sub>y</sub> ( | P<sub>y</sub> (0|b) | ||
Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | ||
Version vom 1. Juni 2021, 06:43 Uhr
1 Zuordnungen und Funktionen
2 Lineare Funktionen
2.1 Lineare Funktionen erkennen und darstellen
2.2 Funktionsgleichung und Funktionsgraph
2.3 Wertetabelle und Funktionsgleichung
2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung
Wiederholung: Erstellen einer Wertetabelle mithilfe der Funktionsgleichung
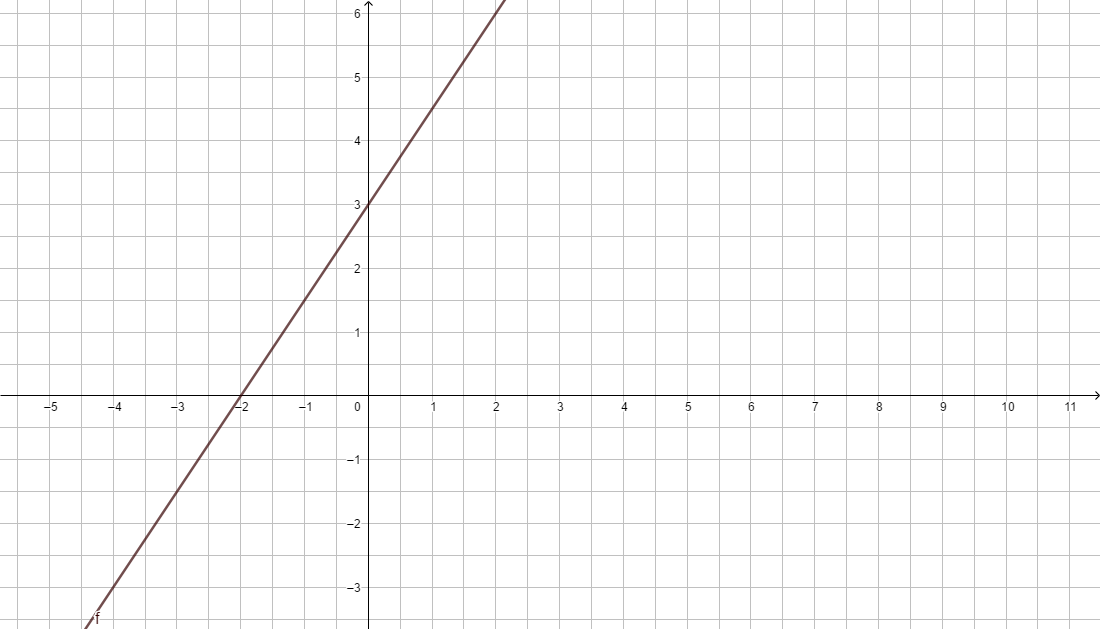
Du hast in den Einführungsbeispielen schon Wertetabellen erstellt. Schauen wir uns das Beispiel zum Bootsverleih noch einmal an. Die Funktionsgleichung lautet f(x) = 2x + 5
Um nun eine Wertetabelle zu erstellen, setze für x verschiedene Werte ein und berechne den zugehörigen y-Wert, den Funktionswert. Erinnerung: Werte von Termen berechnen (7. Klasse)
Das Video fasst das Vorgehen noch einmal zusammen:
Gib die Funktionsgleichungen bei GeoGebra ein und prüfe, ob die von dir errechneten Punkte auf dem Graphen der Funktion liegen.
https://www.geogebra.org/graphing
Punktprobe: Liegt der Punkt auf der Geraden?
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt.
geg: Punkt A(3|10); Funktion f(x) = 2x + 5
ges: Liegt der Punkt A auf dem Graphen der Funktion?
In der Zeichnung erkennen wir sofort, dass dies nicht der Fall ist.
_%3D_2x_%2B_5_Punkt_A_liegt_nicht_auf_dem_Graphen.png)
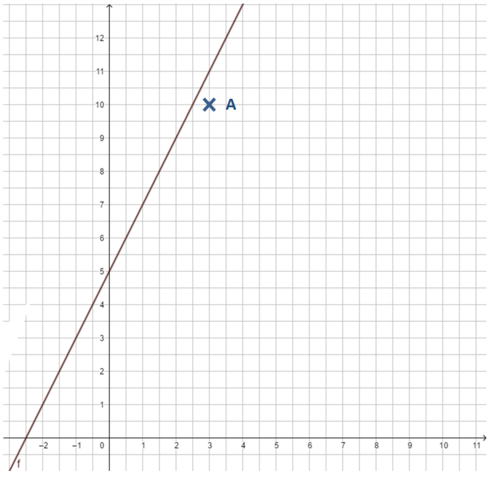
Gegeben ist die Funktionsgleichung y = 2x + 5. Liegt der Punkt A(3|10) auf dem Graphen der Funktion?
(Hier ist es leichter y statt f(x) zu schreiben, der Zusammenhang zu den Koordinaten des Punktes sind dann leichter zu erkennen.)
Idee: Setze die Koordinaten des Punktes in die Funktionsgleichung ein und prüfe, ob die Gleichung erfüllt wird.
y= 2x + 5 A(3|10)
10 = 2·3 + 5
10 = 6 + 5
10 = 11 (f)
Es ergibt sich eine falsche Aussage, die Gleichung ist nicht erfüllt, also liegt der Punkt nicht auf dem Graphen. Wir prüfen ebenso, ob der Punkt B(4|13) auf der Geraden liegt:
Punktprobe:
y = 2x + 5 B(4|13)
13 = 2·4 + 5
13 = 8 + 5
13 = 13 (w)
Es ergibt sich eine wahre Aussage, die Gleichung ist erfüllt, also liegt der Punkt auf dem Graphen.
Das folgende Video fasst noch einmal zusammen:
Fehlende Koordinate eines Punktes der Funktion berechnen
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen.
1. Möglichkeit: x-Koordinate ist gegeben
geg: x = 1,5 und f(x) = 2x+5
ges: zugehöriger y-Wert
Setze die x-Koordinate in die Funktionsgleichung ein und berechne: f(x) = 2x + 5
y = 2·1,5 + 5
= 3 + 5
= 8 P(1,5|8)
Sie müssen 8€ bezahlen.
2. Möglichkeit: y-Koordinate ist gegeben:
Tom und Lisa bezahlen 10 €. Wie lange haben sie das Tretboot ausgeliehen?
geg: y = 10 und f(x) = 2x+5
ges: zugehörige x-Koordinate
Setze die y-Koordinate in die Funktionsgleichung ein und löse nach x auf:
f(x) = 2x + 5
10 = 2x + 5 |-5
5 = 2x |:2
2,5 = x P(2,5|10)
Sie haben das Boot für 2,5 Stunden geliehen.
Hier findest du die Lösungen bunt gemischt:
- fehlende x-Koordinate: 1; 5,5; 8
- fehlende y-Koordinate: -2; 7; 3
Denke daran: P(x/y) Der erste Wert gibt immer die x- und der zweite Wert die y-Koordinate an. Setze nun die entsprechenden Werte für x und y in die Gleichung ein.
- Erhältst du eine wahre Aussage, z.B. 5 = 5, so liegt der Punkt auf dem Funktionsgraphen.
- Erhältst du eine falsche Aussage, z.B. 5 = 8, so liegt der Punkt nicht auf dem Funktionsgraphen.
Hier findest du die Lösungen: (nicht in der richtigen Reihenfolge)
- Punkt A liegt einmal auf dem Graphen, zweimal nicht.
- Punkt B liegt einmal auf dem Graphen, zweimal nicht.
- Punkt C liegt zweimal auf dem Graphen, einmal nicht.
Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben
Die vorangegangenen Übungen zur "Punktprobe" können dir helfen:
Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.Zu Nr. 9: Wenn die Gerade parallel zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden dieselbe Steigung! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b.
Setze die gegebenen Größen ein und löse nach b auf.
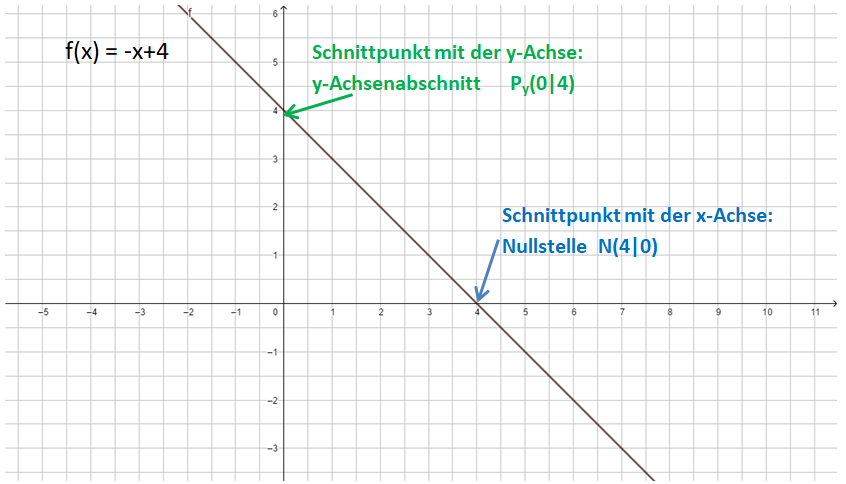
Schnittpunkte mit den Koordinatenachsen bestimmen
Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4
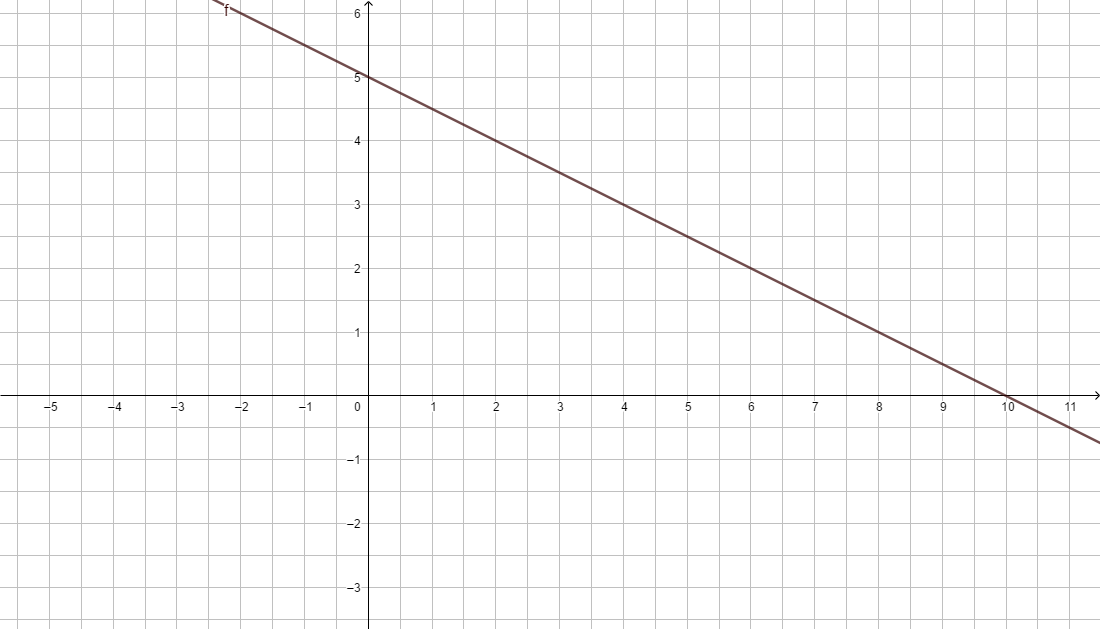
Prüfe dein Ergebnis mithilfe von GeoGebra https://www.geogebra.org/graphing . Gib dort die Funktionsgleichung ein und vergleiche deine rechnerischen Lösungen mit dem Graphen. Wo schneidet der Graph die Koordinatenachsen?_%3D_-x%2B4_Schnittpunkte_mit_den_Koordinatenachsen.png)
_%3D_-0.5x%2B5.png)
_%3D_1.5x%2B3.png)
_%3D_0.25x-2.png)
