Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 440: | Zeile 440: | ||
|Merksatz}} | |Merksatz}} | ||
{{Box|Aufgabe | {{Box|Aufgabe 11: Lückentext zur Lagebeziehung zwischen Ebene und Ebene| | ||
{{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | {{LearningApp|width=100%|height=500px|app=ptpaywm2521}} | ||
| Zeile 453: | Zeile 453: | ||
{{Box | | {{Box |Aufgabe 12: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | ||
'''a)''' | '''a)''' | ||
| Zeile 542: | Zeile 542: | ||
| Hervorhebung1| Farbe={{Farbe|orange}}}} | | Hervorhebung1| Farbe={{Farbe|orange}}}} | ||
{{Box|Aufgabe | {{Box|Aufgabe 13: Ergebnisse interpretieren| | ||
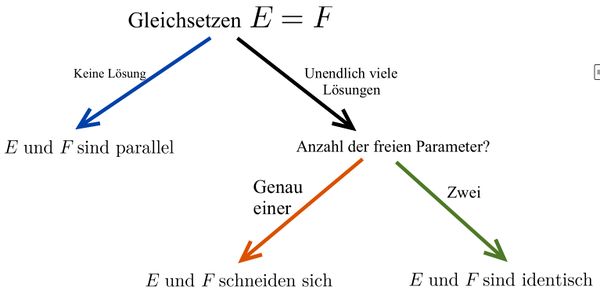
Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch. | Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch. | ||
| Zeile 579: | Zeile 579: | ||
|Merksatz}} | |Merksatz}} | ||
{{Box|⭐Aufgabe: Untersuchung der Lagebeziehung von einer Ebene in Parameterform und einer Ebene in Koordinatenform| | {{Box|⭐Aufgabe 14: Untersuchung der Lagebeziehung von einer Ebene in Parameterform und einer Ebene in Koordinatenform| | ||
'''a'''Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)</math> und eine Ebene <math>F\colon -1{,}5x_1+3x_2-1{,}5x_3=4{,}5</math>. | '''a'''Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)</math> und eine Ebene <math>F\colon -1{,}5x_1+3x_2-1{,}5x_3=4{,}5</math>. | ||
| Zeile 658: | Zeile 658: | ||
Arbeitsmethode|Farbe={{Farbe|orange}}}} | Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
{{Box|⭐Aufgabe | {{Box|⭐Aufgabe 15: Lagebeziehungen untersuchen.| | ||
Untersuche die Lagebeziehung der jeweiligen Ebenen. Falls sich die Ebenen in einer Schnittgerade schneiden, brauchst du diese nicht zu berechnen. | Untersuche die Lagebeziehung der jeweiligen Ebenen. Falls sich die Ebenen in einer Schnittgerade schneiden, brauchst du diese nicht zu berechnen. | ||
| Zeile 763: | Zeile 763: | ||
<math>g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | <math>g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | ||
{{Box|⭐Aufgabe | {{Box|⭐Aufgabe 16: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | ||
Gegeben ist eine Ebene <math>E\colon -2x_1-3x_2+x_3=2</math>. Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld. | Gegeben ist eine Ebene <math>E\colon -2x_1-3x_2+x_3=2</math>. Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld. | ||
| Zeile 783: | Zeile 783: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|⭐Aufgabe | {{Box|⭐Aufgabe 17: Schnitt von zwei Zeltflächen| | ||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. | ||
Version vom 31. Mai 2021, 14:57 Uhr
Lagebeziehung Gerade-Ebene
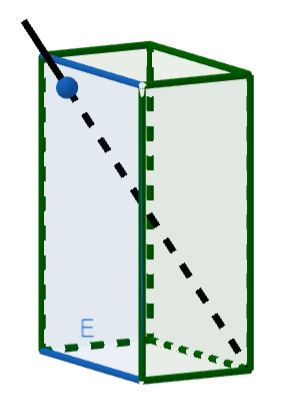
Mögliche Lagebeziehungen zwischen Gerade und Ebene
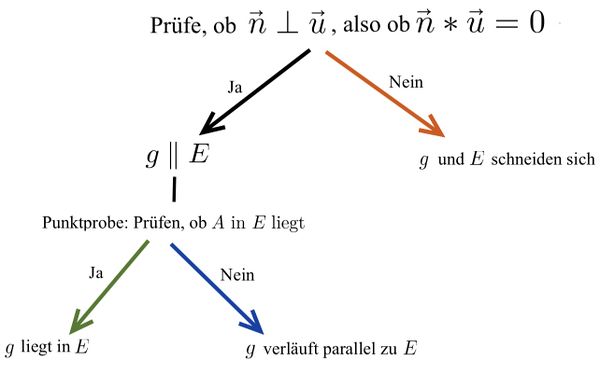
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
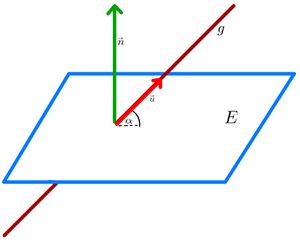
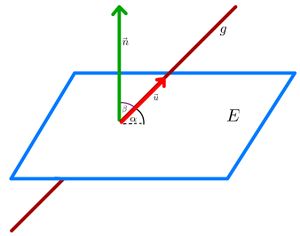
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
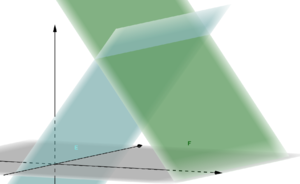
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
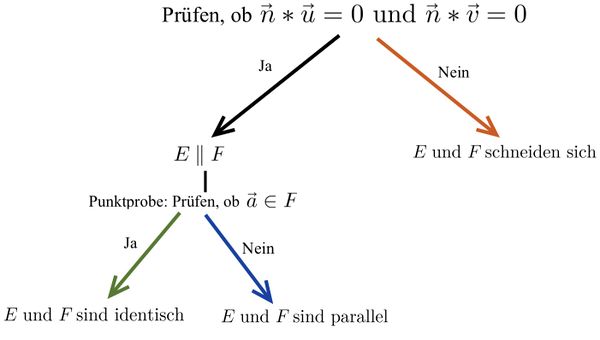
⭐Ebenengleichungen in Parameter- und Koordinatenform
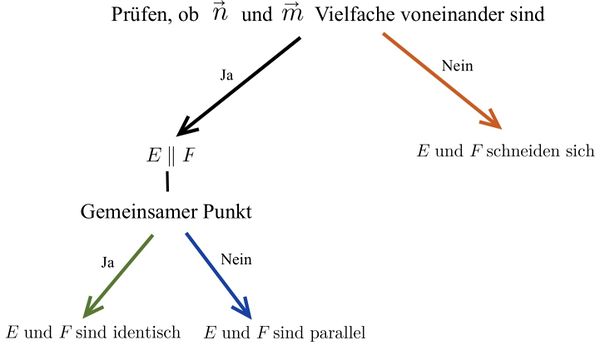
⭐Beide Ebenengleichungen in Koordinatenform
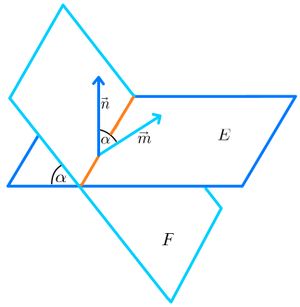
⭐Berechnung des Winkels zwischen Ebene und Ebene