Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 785: | Zeile 785: | ||
{{Box|⭐Aufgabe 12: Schnitt von zwei Zeltflächen| | {{Box|⭐Aufgabe 12: Schnitt von zwei Zeltflächen| | ||
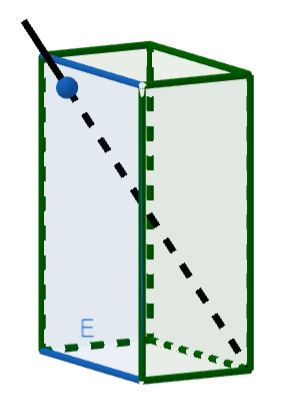
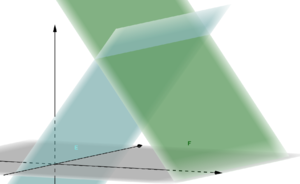
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. [[Datei:Skizze- Schnittgerade zweier Zeltwände.png|mini]] | ||
Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. | |||
In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>50</math> cm entspricht? | In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>50</math> cm entspricht? | ||
{{Lösung versteckt|1= Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen. |2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1= Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen. |2=Tipp | |||
{{Lösung versteckt|1= Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der Schnittgeraden ermitteln. |2=Tipp | {{Lösung versteckt|1= Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der Schnittgeraden ermitteln. |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1= Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante. | {{Lösung versteckt|1= Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante. | ||
| Zeile 800: | Zeile 801: | ||
<math>\begin{vmatrix} 8-r=8-t \\ 3s=6-3u \\ 4s=4u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -r+t=0\\ 3s+3u=6 \\4s-4u=0 \end{vmatrix}</math> | <math>\begin{vmatrix} 8-r=8-t \\ 3s=6-3u \\ 4s=4u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -r+t=0\\ 3s+3u=6 \\4s-4u=0 \end{vmatrix}</math> | ||
<math>\Rightarrow \begin{vmatrix} - | <math>\Rightarrow \begin{vmatrix} -r+t=0 \\ 3s+3u=6 \\ 4s-4u=0\end{vmatrix}</math> | ||
<math>\Rightarrow s=u=1</math> und <math>r=t</math> | <math>\Rightarrow s=u=1</math> und <math>r=t</math> | ||
| Zeile 812: | Zeile 813: | ||
<math>g\colon \vec{x} = \left( \begin{matrix} 8\\ 3\\ 4 \end{matrix} \right) + v \cdot \left( \begin{matrix} -1\\ 0\\ 0 \end{matrix} \right)</math> | <math>g\colon \vec{x} = \left( \begin{matrix} 8\\ 3\\ 4 \end{matrix} \right) + v \cdot \left( \begin{matrix} -1\\ 0\\ 0 \end{matrix} \right)</math> | ||
Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der <math>x_3</math>-Koordinate des Vektors bestimmt werden. | Durch den Richtungsvektor der Geraden wird deutlich, dass sich die Schnittgerade parallel zur <math>x_1x_2</math> -Ebene befindet und somit überall den gleichen Abstand zum Boden hat. Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der <math>x_3</math>-Koordinate des Vektors bestimmt werden. | ||
Die obere Zeltkante befindet sich also in <math>2</math> m Höhe. | Die obere Zeltkante befindet sich also in <math>2</math> m Höhe. | ||
Version vom 31. Mai 2021, 14:44 Uhr
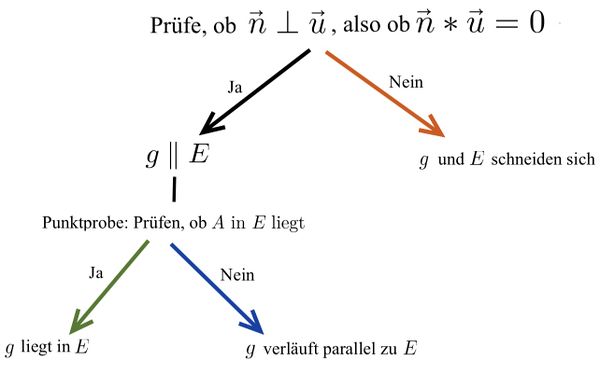
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
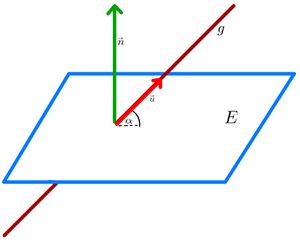
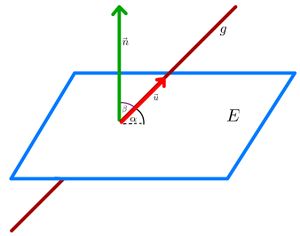
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
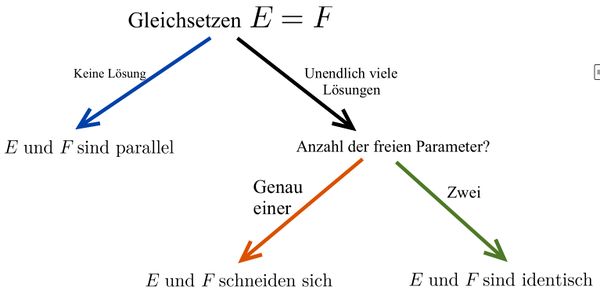
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
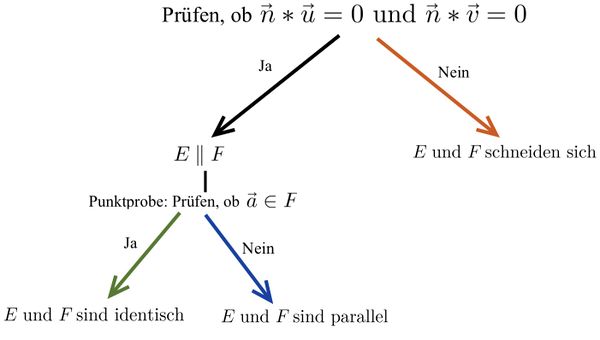
⭐Ebenengleichungen in Parameter- und Koordinatenform
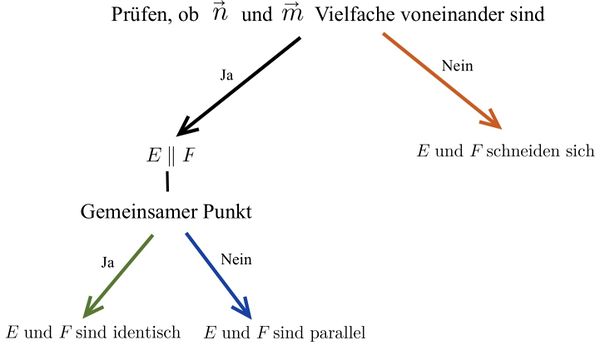
⭐Beide Ebenengleichungen in Koordinatenform
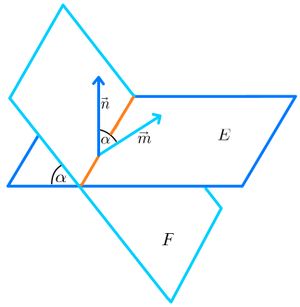
⭐Berechnung des Winkels zwischen Ebene und Ebene