Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 455: | Zeile 455: | ||
{{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | ||
'''a)''' | |||
Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>. | Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>. | ||
Untersuche die Lagebeziehung der beiden Ebenen. | Untersuche die Lagebeziehung der beiden Ebenen. | ||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | '''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | ||
{{Lösung versteckt|1=<math>\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right)= \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | '''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | ||
<math>\begin{vmatrix} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u \\ s-t=3-2r-3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -s+3t-2r+5u=0 \\ {-}2s+t-3r-4u=-2 \\ s-t+2r+3u=3 \end{vmatrix}</math> | {{Lösung versteckt|1=<math>\begin{vmatrix} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u \\ s-t=3-2r-3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -s+3t-2r+5u=0 \\ {-}2s+t-3r-4u=-2 \\ s-t+2r+3u=3 \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | '''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | ||
| Zeile 478: | Zeile 474: | ||
Mithilfe des Gaußverfahrens: | Mithilfe des Gaußverfahrens: | ||
<math>\begin{vmatrix} s+3t-2r+5u=0 \\ 7t-7r-14u=-2 \\ 0=-13\end{vmatrix}</math> | {{Lösung versteckt|1=<math>\begin{vmatrix} s+3t-2r+5u=0 \\ 7t-7r-14u=-2 \\ 0=-13\end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| | | | ||
Mithilfe des Taschenrechners: | Mithilfe des Taschenrechners: | ||
<math>linSolve\begin{pmatrix}\begin{cases} s+3t-2r+5u=0 \\ 7t-7r-14u=-2, \{s,t,r,u\}\\ 0=-13\end{cases} \end{pmatrix}</math> | {{Lösung versteckt|1=<math>linSolve\begin{pmatrix}\begin{cases} s+3t-2r+5u=0 \\ 7t-7r-14u=-2, \{s,t,r,u\}\\ 0=-13\end{cases} \end{pmatrix}</math> | ||
"Keine Lösung gefunden" | "Keine Lösung gefunden"|2=Lösung anzeigen|3=Lösung verbergen}} | ||
}} | }} | ||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
{{Lösung versteckt|1='''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | |||
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch, sodass das LGS keine Lösung besitzt: <math>L=\{\}</math>. Der Taschenrechner zeigt diese Interpretation direkt unterhalb der Lösungsmatrix an. Die beiden Ebenen sind somit parallel.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' | |||
Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 3\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 4\\ 1\\ 3 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 2\\ 4\\ 3 \end{matrix} \right)</math>. | Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 3\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 4\\ 1\\ 3 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 2\\ 4\\ 3 \end{matrix} \right)</math>. | ||
Untersuche die Lagebeziehung der beiden Ebenen. | Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | ||
'''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | '''1. Schritt:''' Setze die beiden Ebenengleichungen gleich. | ||
{{Lösung versteckt|1=<math>\left( \begin{matrix} 1\\ 2\\ 5 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ 1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ 2\\ 4 \end{matrix} \right)= \left( \begin{matrix} 1\\ 3\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} 4\\ 1\\ 3 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 2\\ 4\\ 3\end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | '''2. Schritt:''' Stelle das zugehörige lineare Gleichungssystem auf. | ||
<math>\begin{vmatrix} 1+2r+3s=1+4t+2u \\ 2+3r+2s=3+t+4u \\ 5+r+4s=2+3t+3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1 \\ r+4s-3t-3u=-3 \end{vmatrix}</math> | {{Lösung versteckt|1=<math>\begin{vmatrix} 1+2r+3s=1+4t+2u \\ 2+3r+2s=3+t+4u \\ 5+r+4s=2+3t+3u \end{vmatrix} \Leftrightarrow \begin{vmatrix} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1 \\ r+4s-3t-3u=-3 \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | '''3. Schritt:''' Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: | ||
| Zeile 517: | Zeile 508: | ||
Mithilfe des Gaußverfahrens: | Mithilfe des Gaußverfahrens: | ||
<math>\begin{vmatrix} r+\frac{3}{2}-2t-u=0 \\ s-2t+\frac{2}{5}u=-\frac{2}{5} \\ t-\frac{3}{4}u=-\frac{1}{2} \end{vmatrix}</math> | {{Lösung versteckt|1=<math>\begin{vmatrix} r+\frac{3}{2}-2t-u=0 \\ s-2t+\frac{2}{5}u=-\frac{2}{5} \\ t-\frac{3}{4}u=-\frac{1}{2} \end{vmatrix}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| | | | ||
Mithilfe des Taschenrechners: | Mithilfe des Taschenrechners: | ||
<math>linSolve\begin{pmatrix}\begin{cases} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1, \{r,s,t,u\}\\ r+4s-3t-3u=-3\end{cases} \end{pmatrix}</math> | {{Lösung versteckt|1=<math>linSolve\begin{pmatrix}\begin{cases} 2r+3s-4t-2u=0 \\ 3r+2s-t-4u=1, \{r,s,t,u\}\\ r+4s-3t-3u=-3\end{cases} \end{pmatrix}</math> | ||
<math>\{\}</math>|2=Lösung anzeigen|3=Lösung verbergen}} | |||
}} | }} | ||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
Die Lösungsmenge beträgt: <math>L=\{\}</math>. Die beiden Ebenen schneiden sich in einer Schnittgeraden. | {{Lösung versteckt|1=Die Lösungsmenge beträgt: <math>L=\{\}</math>. Die beiden Ebenen schneiden sich in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''5. Schritt:''' Bestimme die Schnittgerade: | '''5. Schritt:''' Bestimme die Schnittgerade: | ||
Stelle die dritte Gleichung zu <math>t</math> um: | {{Lösung versteckt|1=Stelle die dritte Gleichung zu <math>t</math> um: | ||
<math>t=\frac{3}{4}u-\frac{1}{2}</math> | <math>t=\frac{3}{4}u-\frac{1}{2}</math> | ||
| Zeile 549: | Zeile 540: | ||
Stelle die Schnittgerade auf: | Stelle die Schnittgerade auf: | ||
<math>g\colon \vec{x}=\left( \begin{matrix} \frac{27}{5}\\ {-}\frac{9}{2}\\ {-}\frac{17}{10} \end{matrix} \right) + t \cdot \left( \begin{matrix} 5\\ \frac{19}{4}\\ \frac{21}{4} \end{matrix} \right) </math> | <math>g\colon \vec{x}=\left( \begin{matrix} \frac{27}{5}\\ {-}\frac{9}{2}\\ {-}\frac{17}{10} \end{matrix} \right) + t \cdot \left( \begin{matrix} 5\\ \frac{19}{4}\\ \frac{21}{4} \end{matrix} \right) </math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
Version vom 31. Mai 2021, 12:26 Uhr
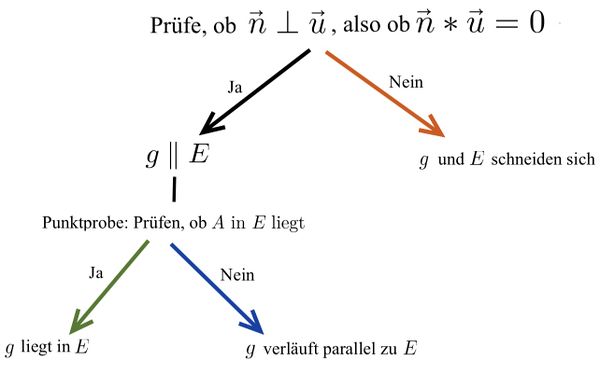
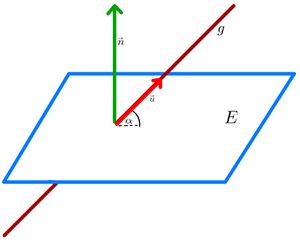
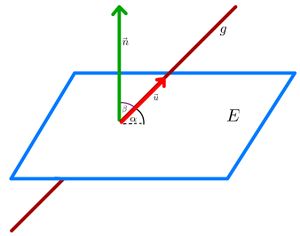
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
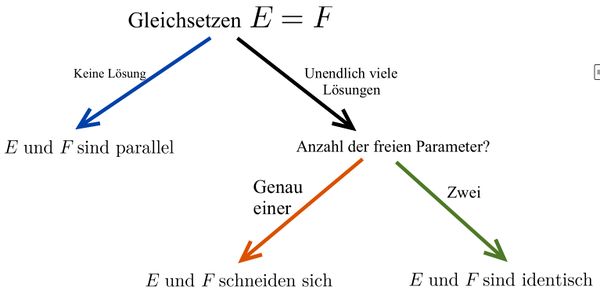
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
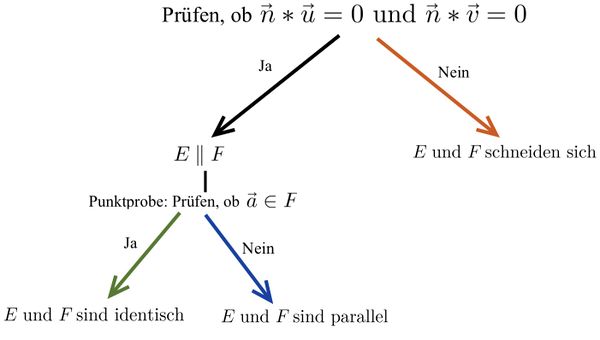
⭐Ebenengleichungen in Parameter- und Koordinatenform
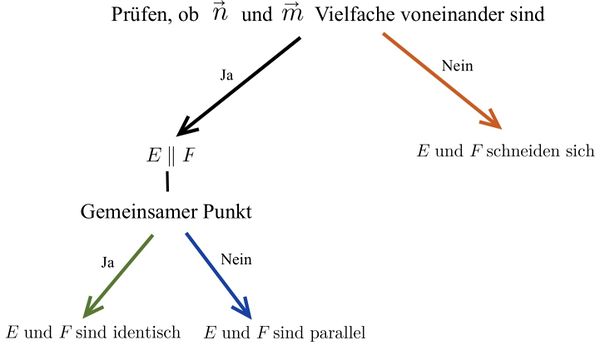
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene