Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 411: | Zeile 411: | ||
Mithilfe des Taschenrechners: | Mithilfe des Taschenrechners: | ||
linSolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u, \{s,t,r,u\}\\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | |||
" | "Keine Lösung gefunden" | ||
}} | }} | ||
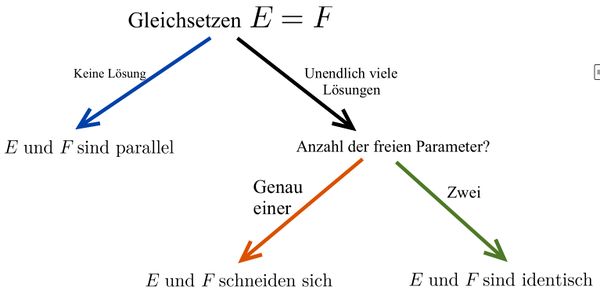
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch, sodass das LGS keine Lösung besitzt: <math>L=\{\}. Der Taschenrechner zeigt diese Interpretation direkt unterhalb der Lösungsmatrix an. Die beiden Ebenen sind somit parallel. | In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch, sodass das LGS keine Lösung besitzt: <math>L=\{\}</math>. Der Taschenrechner zeigt diese Interpretation direkt unterhalb der Lösungsmatrix an. Die beiden Ebenen sind somit parallel. | ||
| Hervorhebung1}} | | Hervorhebung1}} | ||
| Zeile 425: | Zeile 425: | ||
Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch. | Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch. | ||
'''a)''' | '''a)''' | ||
<math> | <math>linSolve\begin{pmatrix}\begin{cases} r-0{,}5u=0{,}5\\ s-u=0{,}5 \{r,s,t,u\}\\ t-1{,}5u=1\end{cases} \end{pmatrix}</math> | ||
<math>\{\}</math> | |||
{{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da nur einer der Parameter frei wählbar ist, schneiden sich die beiden Ebenen in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' | '''b)''' | ||
<math> | <math>linSolve\begin{pmatrix}\begin{cases} r-t-u=2\\ s-t-3u=-5 \{r,s,t,u\}\\ 0=-5\end{cases} \end{pmatrix}</math> | ||
{{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | "Keine Lösung gefunden" | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt keine Lösung, da sich in der dritten Zeile ein Widerspruch befindet. Die Ebenen liegen somit parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''c)''' | '''c)''' | ||
<math> | <math>linSolve\begin{pmatrix}\begin{cases} r-3s-2t-5u=3\\ 7s-7t+14u=7 \{r,s,t,u\}\\0=0\end{cases} \end{pmatrix}</math> | ||
<math>\{\}</math> | |||
{{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da zwei Parameter frei wählbar sind, sind die beiden Ebenen identisch.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
| Zeile 479: | Zeile 484: | ||
Setze hierfür den Aufpunkt der Ebene <math>E</math> in die Ebenengleichung der Ebene <math>F</math> ein. | Setze hierfür den Aufpunkt der Ebene <math>E</math> in die Ebenengleichung der Ebene <math>F</math> ein. | ||
<math>-1{,}5\cdot2+3\cdot1-1{,}5\cdot(-3)=4{,}5 \checkmark</math> | <math>-1{,}5\cdot2+3\cdot1-1{,}5\cdot(-3)=4{,}5\checkmark</math> | ||
| Zeile 518: | Zeile 523: | ||
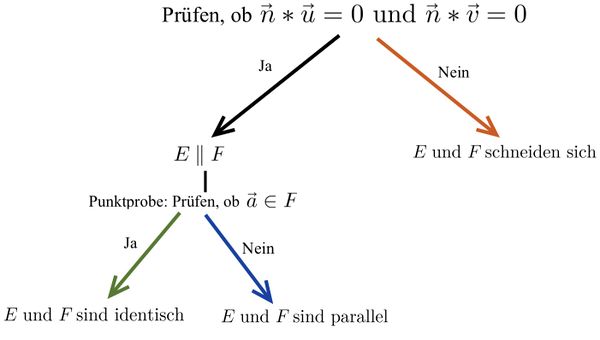
<math>\vec{n} \ast \vec{v}=\left( \begin{matrix} {-}1\\ 0\\ 3\end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0</math> | <math>\vec{n} \ast \vec{v}=\left( \begin{matrix} {-}1\\ 0\\ 3\end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0</math> | ||
Da | Da beide Skalarprodukte der jeweiligen Vektoren <math>0</math> sind, liegt der Normalenvektor orthogonal zu beiden Richtungsvektoren. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind. | ||
Punktprobe:<math>-3\cdot({-}3)-9\cdot1-0=-18\neq5</math> | Punktprobe:<math>-3\cdot({-}3)-9\cdot1-0=-18\neq5</math> | ||
| Zeile 532: | Zeile 537: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{ | Prüfe, ob die Richtungsvektoren <math>\vec{u}</math> und <math>\vec{v}</math> der Ebene <math>E</math> orthogonal zum Normalenvektor <math>\vec{n}</math> der Ebene <math>F</math> liegen. | ||
<math>\vec{n} \ast \vec{u}=\left( \begin{matrix} -1 \\ 0 \\ {-}0{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | <math>\vec{n} \ast \vec{u}=\left( \begin{matrix} -1 \\ 0 \\ {-}0{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | ||
| Zeile 538: | Zeile 543: | ||
<math>\vec{n} \ast \vec{v}=\left( \begin{matrix} 4 \\ 2 \\ 1 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | <math>\vec{n} \ast \vec{v}=\left( \begin{matrix} 4 \\ 2 \\ 1 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0</math> | ||
Da | Da beide Skalarprodukte der jeweiligen Vektoren <math>0</math> sind, liegt der Normalenvektor orthogonal zu beiden Richtungsvektoren. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind. | ||
Punktprobe:<math>2\cdot2-2\cdot(-1)-3\cdot4=-6\ | Punktprobe:<math>2\cdot2-2\cdot(-1)-3\cdot4=-6\checkmark</math> | ||
Da die Koordinatengleichung von <math>F</math> erfüllt wird, liegt <math>E</math> in <math>F</math> und die Ebenen sind identisch. | Da die Koordinatengleichung von <math>F</math> erfüllt wird, liegt <math>E</math> in <math>F</math> und die Ebenen sind identisch. | ||
| Zeile 561: | Zeile 566: | ||
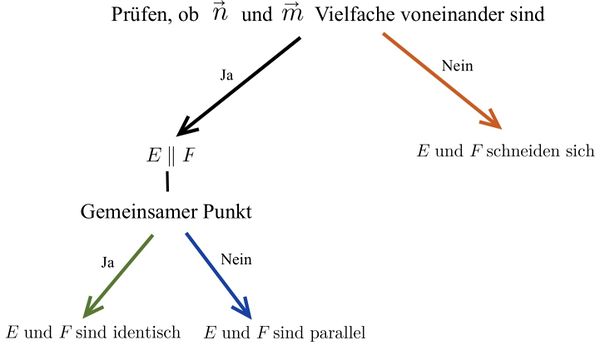
'''1. Schritt:''' Prüfe, ob der Normalenvektor <math>\vec{n}</math> der Ebene <math>E</math> ein Vielfaches des Normalenvektors <math>\vec{m}</math> der Ebene <math>F</math> ist. | '''1. Schritt:''' Prüfe, ob der Normalenvektor <math>\vec{n}</math> der Ebene <math>E</math> ein Vielfaches des Normalenvektors <math>\vec{m}</math> der Ebene <math>F</math> ist. | ||
<math> | Bei der Betrachtung der Normalenvektoren <math>\vec{n}=\left( \begin{matrix} 3\\ {-}4\\ {-}1 \end{matrix} \right)</math> und <math>\vec{m}=\left( \begin{matrix} 3\\ {-}3\\ 1 \end{matrix} \right) </math> fällt direkt auf, dass die beiden Vektoren keine Vielfachen voneinander sind. Man kann also direkt schließen, dass sich die beiden Ebenen in einer Schnittgeraden schneiden. Ein formaler Nachweis würde wie folgt aussehen: | ||
<math>r\cdot\vec{n}=\vec{m} \Leftrightarrow r\cdot\left( \begin{matrix} 3\\ {-}4\\ {-}1 \end{matrix} \right)=\left( \begin{matrix} 3\\ {-}3\\ 1 \end{matrix} \right) \Leftrightarrow \begin{vmatrix} 3r=3\\ {-}4r=-3 \\ {-}r=1 \end{vmatrix}</math> | |||
Da das LGS nicht lösbar ist, sind die Gleichungen keine Vielfachen voneinander und die Ebenen schneiden sich in einer Schnittgeraden. | |||
'''2. Schritt:''' Bestimme die Schnittgerade. | |||
Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algorithmus oder dem Taschenrechner. | |||
{{2Spalten | |||
| | |||
Mithilfe des Gaußverfahrens: | |||
<math>\begin{vmatrix} 3x_1-4x_2-x_3=4 \\ 3x_1-3x_2+x_3=3\end{vmatrix} \Leftrightarrow \begin{vmatrix} 3x_1-4x_2-x_3=4 \\ x_2+2x_3=-1\end{vmatrix}</math> | |||
| | |||
Mithilfe des Taschenrechners: | |||
linSolve<math>\begin{pmatrix}\begin{cases} 3x_1-4x_2-x_3=4 \\ 3x_1-3x_2+x_3=3,\{s,t,r,u\}\end{cases} \end{pmatrix}</math> | |||
\{\} | |||
}} | |||
Setze <math>x_3=t</math> und bestimme <math>x_1</math> und <math>x_2</math>. | Setze <math>x_3=t</math> und bestimme <math>x_1</math> und <math>x_2</math>. | ||
| Zeile 579: | Zeile 594: | ||
<math>x_2=-1-2t</math> | <math>x_2=-1-2t</math> | ||
<math>x_1=-\frac{7}{3}</math> | <math>x_1=-\frac{7}{3}t</math> | ||
Stelle die Geradengleichung auf. | Stelle die Geradengleichung auf. | ||
| Zeile 605: | Zeile 620: | ||
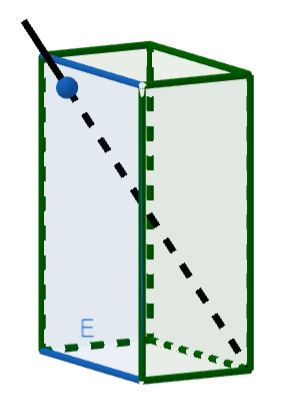
{{Box|⭐Aufgabe 12: Schnitt von zwei Zeltflächen| | {{Box|⭐Aufgabe 12: Schnitt von zwei Zeltflächen| | ||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math> | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}</math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1x_2</math> -Ebene aufgespannt. In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>50</math> cm entspricht? | ||
{{Lösung versteckt|1= Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1= Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
Version vom 24. Mai 2021, 13:25 Uhr
Lagebeziehung Gerade-Ebene
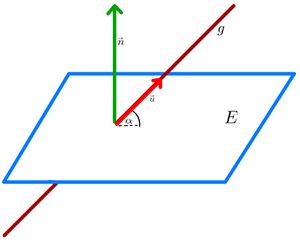
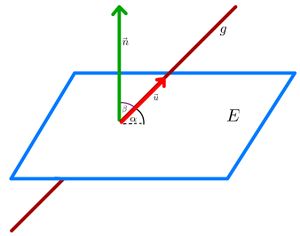
Mögliche Lagebeziehungen zwischen Gerade und Ebene
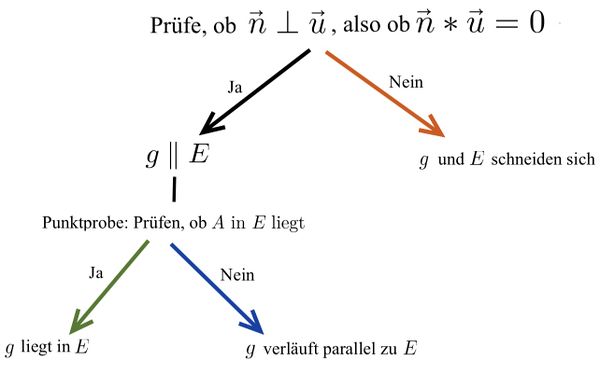
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
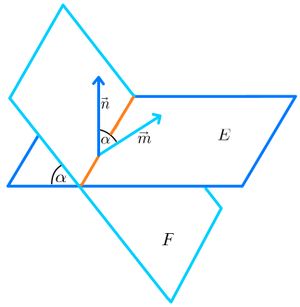
⭐Berechnung des Winkels zwischen Ebene und Ebene