Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2.3 Wertetabelle und Funktionsgleichung: Unterschied zwischen den Versionen
K (formale Korrektur Tipps 8, 9) Markierung: Quelltext-Bearbeitung 2017 |
K (Übung 10 (realmath-Übungen zu Koordinaten berechnen + Punktprobe) eingefügt + anschließende Nummerierung geändert) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 148: | Zeile 148: | ||
* Punkt B liegt einmal auf dem Graphen, zweimal nicht. | * Punkt B liegt einmal auf dem Graphen, zweimal nicht. | ||
* Punkt C liegt zweimal auf dem Graphen, einmal nicht.|2=Lösungzu Nr. 9|3=Lösung ausblenden}} | * Punkt C liegt zweimal auf dem Graphen, einmal nicht.|2=Lösungzu Nr. 9|3=Lösung ausblenden}} | ||
{{Box| Übung 10: Fehlende Koordinaten bestimmen und Punktprobe | <br> | |||
* [http://realmath.de/Neues/Klasse8/linearefunktion/koordberechnen.php] <br> | |||
* [http://realmath.de/Neues/Klasse8/linearefunktion/liegtpaufg.php]|Üben}} | |||
<br /> | <br /> | ||
| Zeile 154: | Zeile 161: | ||
===Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben=== | ===Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben=== | ||
<br> | <br> | ||
{{Box| Übung | {{Box| Übung 11: Aufstellen der Funktionsgleichung | Löse S. 130 Nr. 9 (zeichnerisch UND rechnerisch) und S. 131 Nr. 13. Gegeben ist ein Punkt und die Steigung bzw. der y-Achsenabschnitt b. Wie kannst du vorgehen?|Üben}} | ||
{{Lösung versteckt|1= Die vorangegangenen Übungen zur "Punktprobe" können dir helfen: | {{Lösung versteckt|1= Die vorangegangenen Übungen zur "Punktprobe" können dir helfen: | ||
| Zeile 179: | Zeile 186: | ||
{{LearningApp|app=pu8028csj20|width=100%|height=400px}} | {{LearningApp|app=pu8028csj20|width=100%|height=400px}} | ||
{{Box|Übung | {{Box|Übung 12: Schnittpunkte mit den Koordinatenachsen|Löse S. 137 Nr. 7|Üben}} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
{{Lösung versteckt|1=Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0 | {{Lösung versteckt|1=Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0 | ||
Version vom 24. Mai 2021, 13:04 Uhr
1 Zuordnungen und Funktionen
2 Lineare Funktionen
2.1 Lineare Funktionen erkennen und darstellen
2.2 Funktionsgleichung und Funktionsgraph
2.3 Wertetabelle und Funktionsgleichung
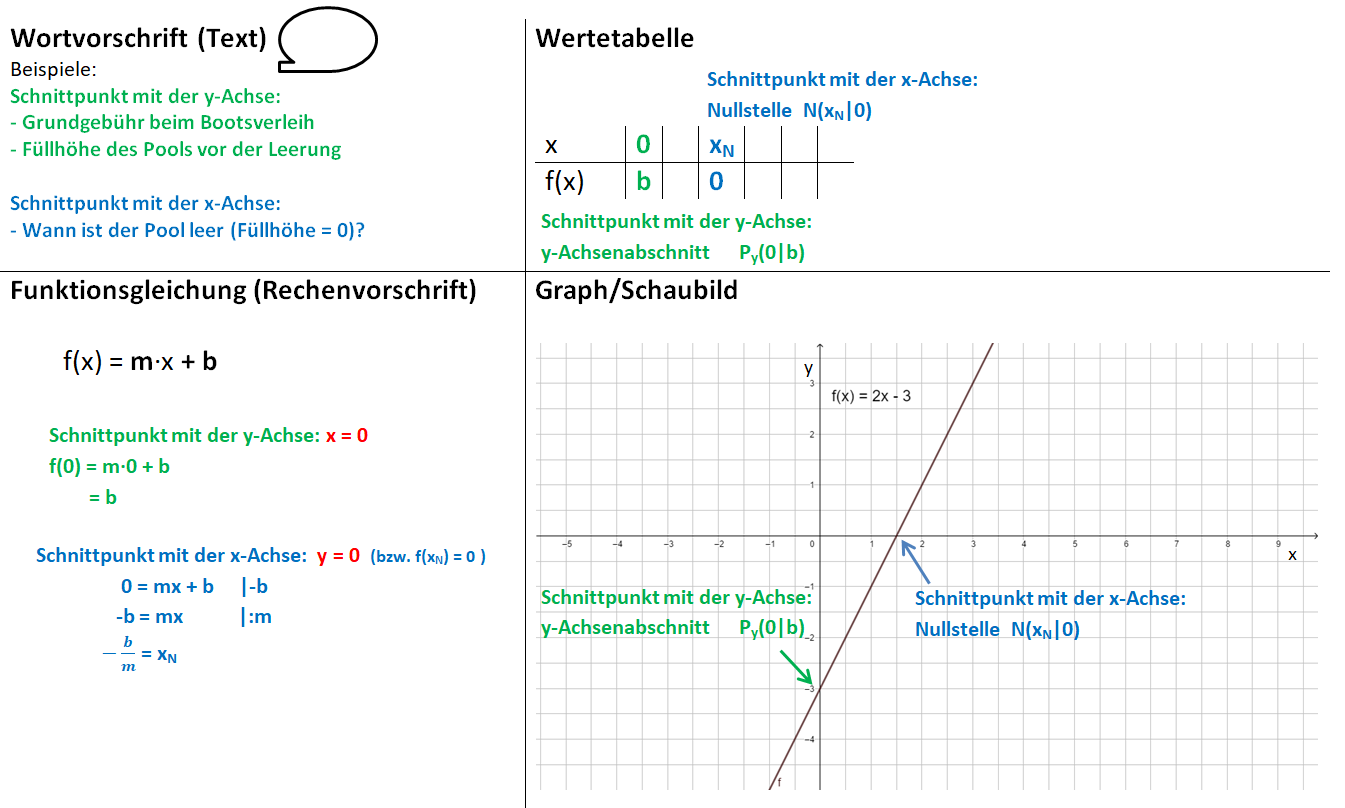
2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung
Wiederholung: Erstellen einer Wertetabelle mithilfe der Funktionsgleichung
Du hast in den Einführungsbeispielen schon Wertetabellen erstellt. Schauen wir uns das Beispiel zum Bootsverleih noch einmal an. Die Funktionsgleichung lautet f(x) = 2x + 5
Um nun eine Wertetabelle zu erstellen, setze für x verschiedene Werte ein und berechne den zugehörigen y-Wert, den Funktionswert. Erinnerung: Werte von Termen berechnen (7. Klasse)

Das Video fasst das Vorgehen noch einmal zusammen:
Gib die Funktionsgleichungen bei GeoGebra ein und prüfe, ob die von dir errechneten Punkte auf dem Graphen der Funktion liegen.
https://www.geogebra.org/graphing
Punktprobe: Liegt der Punkt auf der Geraden?
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt.
Tom und Lisa leihen für 3 Stunden ein Tretboot. Der Bootsverleiher rechnet den Preis 10€ aus. Kann das sein?
geg: Punkt A(3|10); Funktion f(x) = 2x + 5
ges: Liegt der Punkt A auf dem Graphen der Funktion?
In der Zeichnung erkennen wir sofort, dass dies nicht der Fall ist.
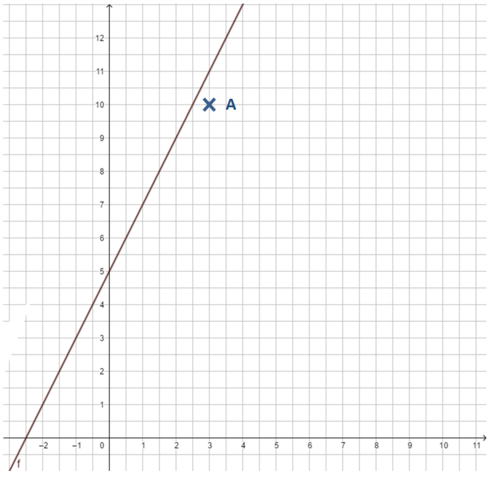
Gegeben ist die Funktionsgleichung y = 2x + 5. Liegt der Punkt A(3|10) auf dem Graphen der Funktion?
(Hier ist es leichter y statt f(x) zu schreiben, der Zusammenhang zu den Koordinaten des Punktes sind dann leichter zu erkennen.)
Idee: Setze die Koordinaten des Punktes in die Funktionsgleichung ein und prüfe, ob die Gleichung erfüllt wird.
y= 2x + 5 A(3|10)
10 = 2·3 + 5
10 = 6 + 5
10 = 11 (f)
Es ergibt sich eine falsche Aussage, die Gleichung ist nicht erfüllt, also liegt der Punkt nicht auf dem Graphen. Wir prüfen ebenso, ob der Punkt B(4|13) auf der Geraden liegt:
Punktprobe:
y = 2x + 5 B(4|13)
13 = 2·4 + 5
13 = 8 + 5
13 = 13 (w)
Es ergibt sich eine wahre Aussage, die Gleichung ist erfüllt, also liegt der Punkt auf dem Graphen.
Das folgende Video fasst noch einmal zusammen:
Fehlende Koordinate eines Punktes der Funktion berechnen
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen.
1. Möglichkeit: x-Koordinate ist gegeben
Tom und Lisa leihen ein Tretboot für 1,5 Stunden. Wie viel müssen sie bezahlen?
geg: x = 1,5 und f(x) = 2x+5
ges: zugehöriger y-Wert
Setze die x-Koordinate in die Funktionsgleichung ein und berechne: f(x) = 2x + 5
y = 2·1,5 + 5
= 3 + 5
= 8 P(1,5|8)
Sie müssen 8€ bezahlen.
2. Möglichkeit: y-Koordinate ist gegeben:
Tom und Lisa bezahlen 10 €. Wie lange haben sie das Tretboot ausgeliehen?
geg: y = 10 und f(x) = 2x+5
ges: zugehörige x-Koordinate
Setze die y-Koordinate in die Funktionsgleichung ein und löse nach x auf:
f(x) = 2x + 5
10 = 2x + 5 |-5
5 = 2x |:2
2,5 = x P(2,5|10)
Sie haben das Boot für 2,5 Stunden geliehen.
Hier findest du die Lösungen bunt gemischt:
- fehlende x-Koordinate: 1; 5,5; 8
- fehlende y-Koordinate: -2; 7; 3
Denke daran: P(x/y) Der erste Wert gibt immer die x- und der zweite Wert die y-Koordinate an. Setze nun die entsprechenden Werte für x und y in die Gleichung ein.
- Erhältst du eine wahre Aussage, z.B. 5 = 5, so liegt der Punkt auf dem Funktionsgraphen.
- Erhältst du eine falsche Aussage, z.B. 5 = 8, so liegt der Punkt nicht auf dem Funktionsgraphen.
Hier findest du die Lösungen: (nicht in der richtigen Reihenfolge)
- Punkt A liegt einmal auf dem Graphen, zweimal nicht.
- Punkt B liegt einmal auf dem Graphen, zweimal nicht.
- Punkt C liegt zweimal auf dem Graphen, einmal nicht.
Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben
Die vorangegangenen Übungen zur "Punktprobe" können dir helfen:
Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.Zu Nr. 9: Wenn die Gerade parallel zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden dieselbe Steigung! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b.
Setze die gegebenen Größen ein und löse nach b auf.
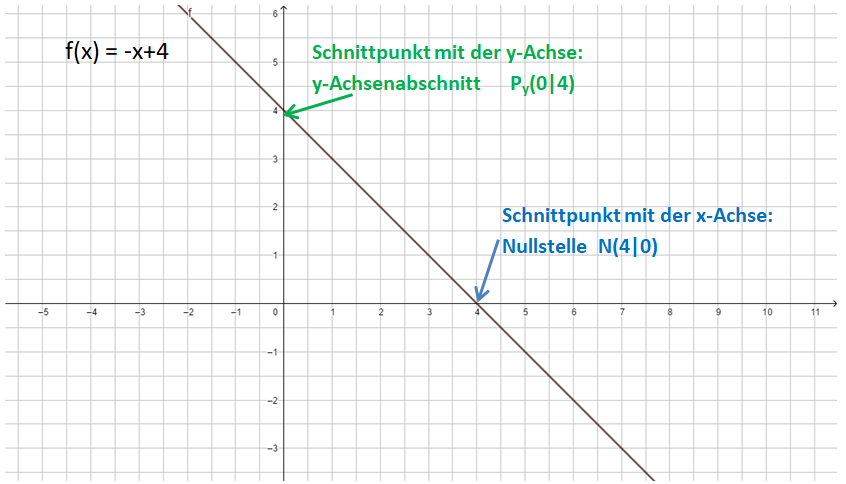
Schnittpunkte mit den Koordinatenachsen bestimmen
Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4
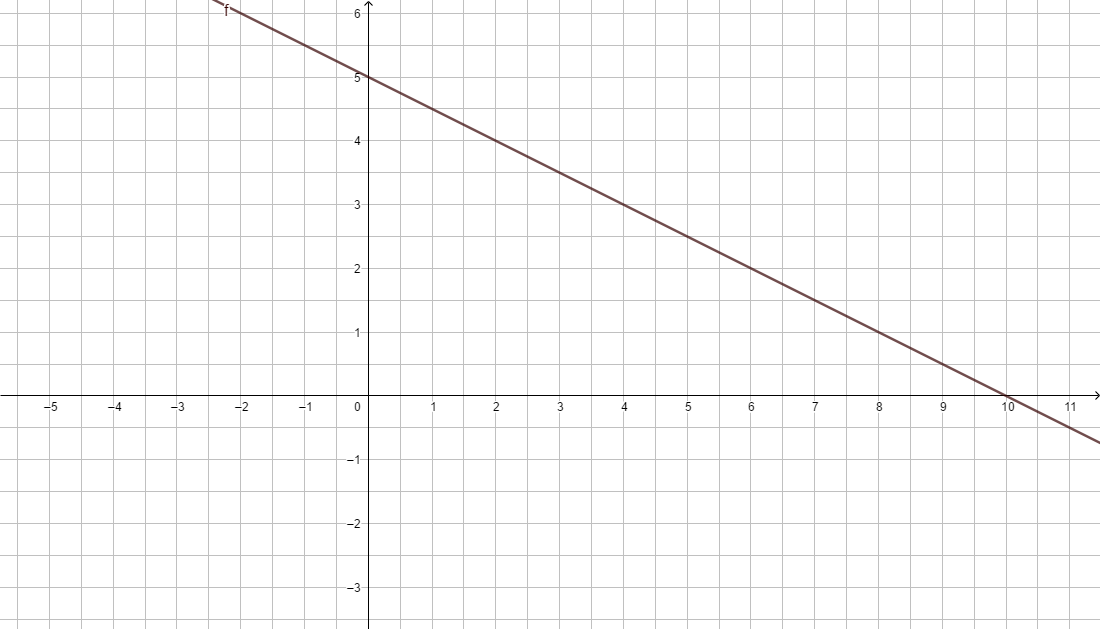
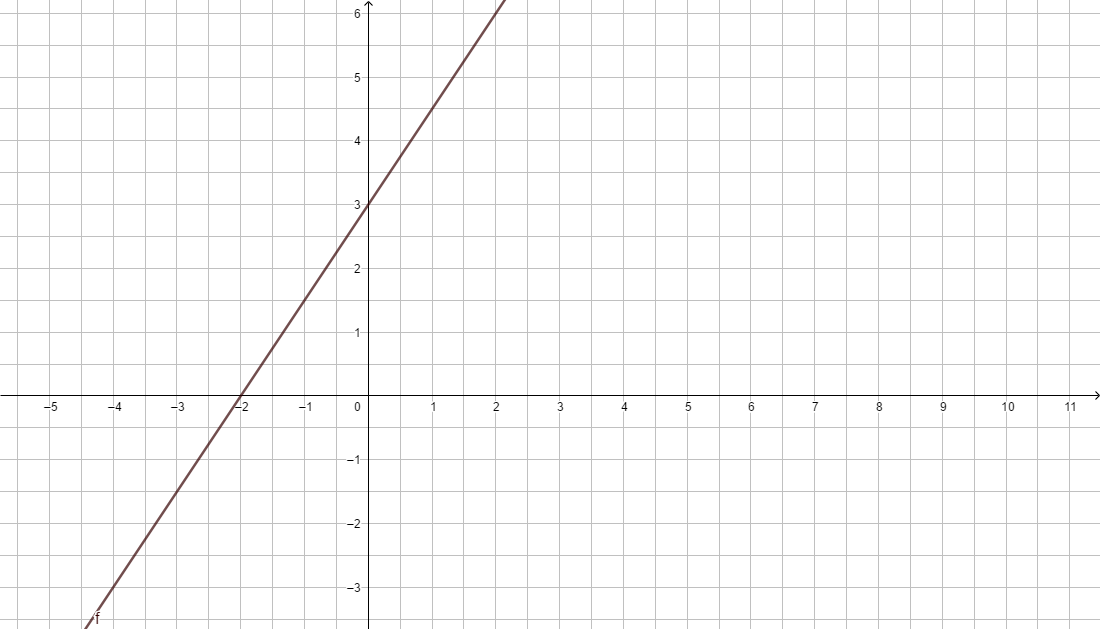
Prüfe dein Ergebnis mithilfe von GeoGebra https://www.geogebra.org/graphing . Gib dort die Funktionsgleichung ein und vergleiche deine rechnerischen Lösungen mit dem Graphen. Wo schneidet der Graph die Koordinatenachsen?