Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 411: | Zeile 411: | ||
Mithilfe des Taschenrechners: | Mithilfe des Taschenrechners: | ||
linsolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u \\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | linsolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u <math>\{s,t,r,u\}\\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | ||
"keine Lösung gefunden" | "keine Lösung gefunden" | ||
}} | }} | ||
'''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | '''4. Schritt:''' Interpretiere die Lösung des Gleichungssystems: | ||
| Zeile 424: | Zeile 424: | ||
{{Box|Aufgabe 9: Ergebnisse interpretieren| | {{Box|Aufgabe 9: Ergebnisse interpretieren| | ||
Zur Untersuchung der Lagebeziehung zweier Ebenen, wurden die Ebenengleichungen gleichgesetzt und das zugehörige Gleichungssystem aufgestellt. Betrachte die Ausgabe des Taschenrechners und interpretiere die jeweilige Situation geometrisch. | |||
'''a)''' | |||
<math>linsolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u <math>\{s,t,r,u\}\\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | |||
{{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | |||
'''b)''' | |||
<math>linsolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u <math>\{s,t,r,u\}\\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''c)''' | |||
<math>linsolve<math>\begin{pmatrix}\begin{cases} 1+s+3t=1+2r+5u \\ 4-2s+t=2+3r+4u <math>\{s,t,r,u\}\\ s-t=3-2r-3u\end{cases} \end{pmatrix}</math> | |||
{{Lösung versteckt|1=|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
| Zeile 549: | Zeile 555: | ||
{{Box | ⭐Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform | | {{Box | ⭐Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform | | ||
Gegeben sind eine Ebene <math>E\colon 3x_1-4x_2-x_3=4</math> und eine Ebene <math>F\colon 3x_1-3x_2+x_3=3</math>. Untersuche die Lagebeziehung der beiden Ebenen. | Gegeben sind eine Ebene <math>E\colon 3x_1-4x_2-x_3=4</math> und eine Ebene <math>F\colon 3x_1-3x_2+x_3=3</math>. Untersuche die Lagebeziehung der beiden Ebenen und berechne gegebenenfalls die Schnittgerade. | ||
| Zeile 584: | Zeile 590: | ||
{{LearningApp|width=100%|height=500px|app=pq97ryxmn21}} | {{LearningApp|width=100%|height=500px|app=pq97ryxmn21}} | ||
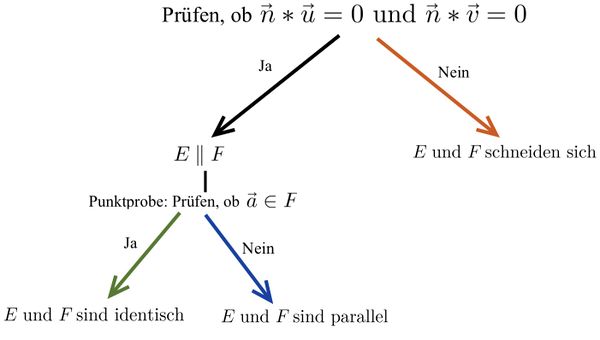
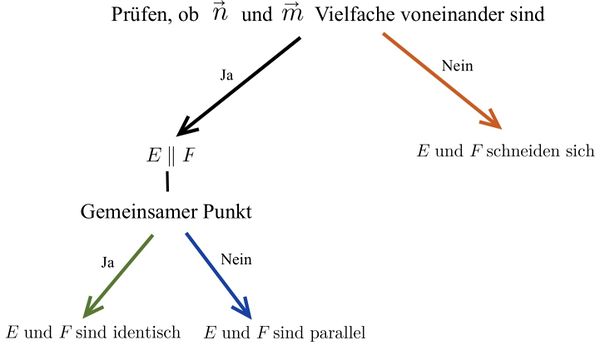
{{Lösung versteckt|1= Um die Lagebeziehung von zwei Ebenen in Koordinatenform zu bestimmen, benötigst du keinen Taschenrechner.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1= Um die Lagebeziehung von zwei Ebenen in Koordinatenform zu bestimmen, benötigst du keinen Taschenrechner. Schaue dir die beiden Gleichungen gut an.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Vergleiche die Gleichungen der zwei Ebenen miteinander. | Vergleiche die Gleichungen der zwei Ebenen miteinander. | ||
Die Ebenen schneiden sich, wenn die beiden Gleichungen | Die Ebenen schneiden sich, wenn die beiden Gleichungen keine Vielfachen voneinander sind. | ||
Die Ebenen sind parallel, wenn die Normalenvektoren identisch oder Vielfache voneinander sind, aber das LGS keine Lösung besitzt. | Die Ebenen sind parallel, wenn die Normalenvektoren identisch oder Vielfache voneinander sind, aber das LGS keine Lösung besitzt. | ||
Die Ebenen sind identisch, wenn die Normalenvektoren identisch oder Vielfache voneinander sind und das LGS somit unendlich viele Lösungen hat. | |||
|2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | |2=Tipp 2 anzeigen|3=Tipp 2 verbergen}} | ||
Version vom 22. Mai 2021, 11:44 Uhr
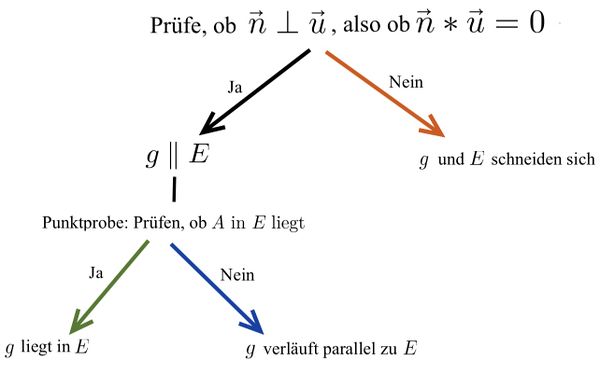
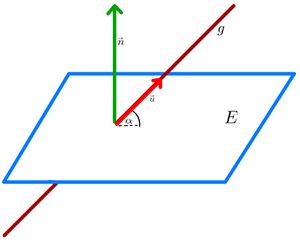
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
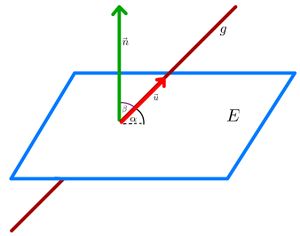
⭐Berechnung des Winkels zwischen Gerade und Ebene
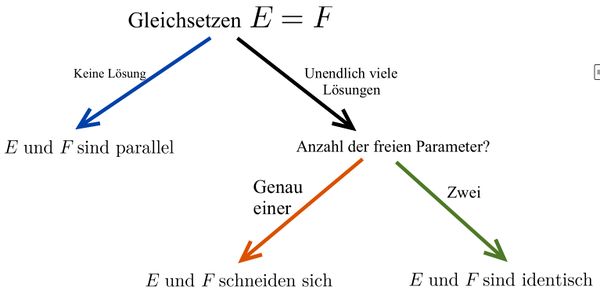
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene