Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 230: | Zeile 230: | ||
{{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | {{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | ||
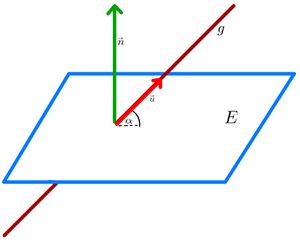
[[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg| rechts | mini | Winkel zwischen Gerade und Ebene]] | [[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg| rechts | mini |Abbildung: Winkel zwischen Gerade und Ebene]] | ||
Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>\vec{n}</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>\vec{u}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math>\sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math>. | Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>\vec{n}</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>\vec{u}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math>\sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math>. | ||
Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. | Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. Dein berechneter Winkel <math>\alpha</math> darf also nur zwischen <math>0^{\circ}</math> und <math>90^{\circ}</math> liegen. Ist dein berechneter Winkel <math>\alpha > 90^{\circ}</math>, so musst du <math>180^{\circ} - \alpha</math> berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen. | ||
Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen: | Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen: | ||
| Zeile 240: | Zeile 240: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
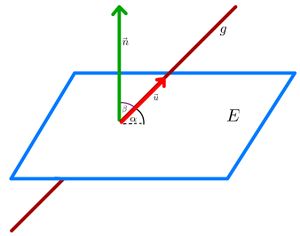
[[Datei:Abbildung- Winkel zwischen Gerade und Ebene, Zusammenhang zum Normalenvektor.jpg | rechts | mini | Winkel zwischen Gerade und Ebene]] | [[Datei:Abbildung- Winkel zwischen Gerade und Ebene, Zusammenhang zum Normalenvektor.jpg | rechts | mini | Abbildung: Winkel zwischen Gerade und Ebene]] | ||
Der Normalenvektor <math>\vec{n}</math> einer Ebene steht in einem <math>90^{\circ} </math> Winkel zur Ebene <math>E</math>. | Der Normalenvektor <math>\vec{n}</math> einer Ebene steht in einem <math>90^{\circ} </math> Winkel zur Ebene <math>E</math>. | ||
| Zeile 247: | Zeile 247: | ||
| Merksatz}} | | Merksatz}} | ||
{{Box | Beispiel: Berechnung des Winkels zwischen Gerade und Ebene | | {{Box | Beispiel: Berechnung des Winkels zwischen Gerade und Ebene | | ||
Version vom 19. Mai 2021, 17:58 Uhr
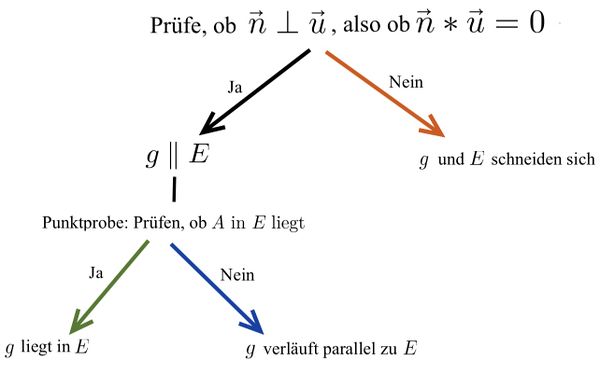
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
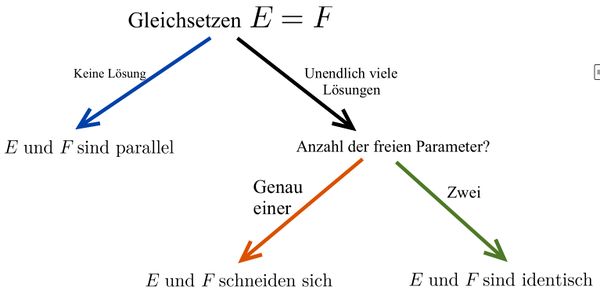
Beide Ebenengleichungen in Parameterform
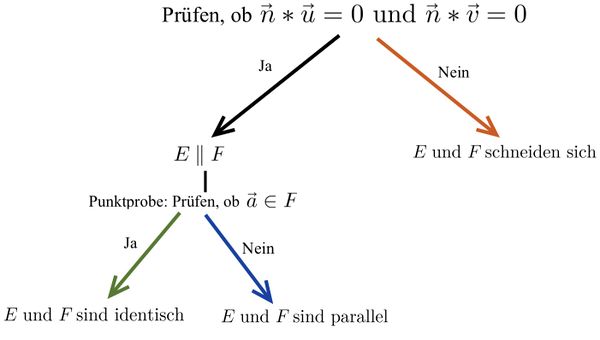
⭐Ebenengleichungen in Parameter- und Koordinatenform
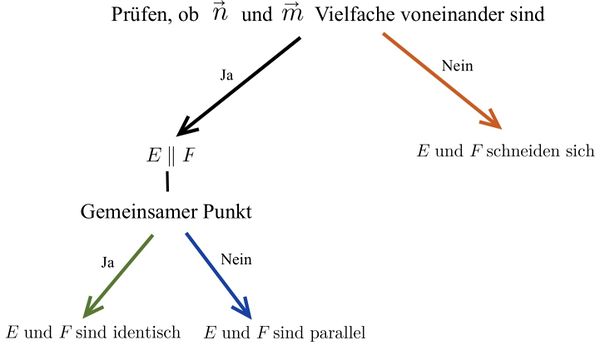
⭐Beide Ebenengleichungen in Koordinatenform
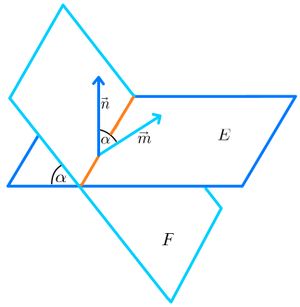
⭐Berechnung des Winkels zwischen Ebene und Ebene