Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum

Info

In diesem Lernpfadkapitel kannst du das Thema "Abstände von Objekten im Raum" wiederholen und vertiefen.

Wie du im Inhaltsverzeichnis siehst, gibt es drei Abschnitte: einen zum Abstand zwischen einer Ebene und einem Punkt, einen zum Abstand zwischen einer Geraden und einem Punkt und einen dritten zum Abstand zwischen zwei windschiefen Geraden. Suche dir einfach aus, was du üben möchtest. Es gibt auch Knobelaufgaben. Vorher kannst du noch die Einstiegsaufgabe machen, um deine generelle inhaltliche Vorstellung zu testen.

Dieses Thema ist nur für den LK gedacht, daher sind alle Aufgaben auch automatisch LK-Aufgaben und nicht noch jeweils mit einem ⭐ gekennzeichnet.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg und Spaß!

Einstieg

Aufgabe 1

Zu welcher Sachsituation passen die Rechenschritte jeweils? Ordne zu.

1. Zwei Kinder befinden sich im Klettergarten auf zwei verschiedenen Seilen. Wo auf ihrem Seil müssen sie sein, damit sie sich am nächsten sind? Wie nah sind sie sich dann?

2. Bei einem alten Haus soll bei der Renovierung ein Stützbalken vom Boden im Dachgeschoss zur oberen Dachkante gebaut werden. Er soll senkrecht auf dem Fußboden stehen. Wie lang muss er sein?

Dachboden

3.Luke Skywalker fliegt in seinem Raumschiff zum Auskundschaften am Todesstern vorbei. Dieser befindet sich im Verhältnis zur geradlinigen Bewegung des Raumschiffs in Ruhe. Der Sensor auf dem Todesstern hat eine Reichweite von $10km$. Wird Luke mit seinem Raumschiff entdeckt?

A. $h:\vec{x}=\begin{pmatrix} 2 \\ 0 \\ 15 \end{pmatrix}+s\cdot\begin{pmatrix} 0 \\ 0 \\ -3 \end{pmatrix}$ ist die zu $E: x_3=10$ orthogonale Gerade durch einen Punkt von $g$. Wegen $15-3s=10$, also $s=\frac{5}{3}$, erhält man den Lotfußpunkt $(2|0|10)$.

B. $h:\vec{x}=\begin{pmatrix} 5 \\ -16 \\ 3 \end{pmatrix}+s\cdot\begin{pmatrix} -10 \\ -22 \\ 86 \end{pmatrix}$ ist die Gerade, die den Punkt $P(30|22|-55)$ und einem Punkt $L$ auf der Geraden $g:\vec{x}=\begin{pmatrix} 5 \\ -16 \\ 3 \end{pmatrix}+s\cdot\begin{pmatrix} 20 \\ 0 \\ 31 \end{pmatrix}$ in Abhängigkeit vom Geradenparameter $s$ verbindet. Damit $h$ orthogonal zu $g$ ist, muss $s=6,75$ sein und $L$ ist somit $(140|-16|212,25)$.

C.$G(4|-10|19)$ ist der Lotfußpunkt auf $g$ und $H(-2|-12|22)$ ist der Lotfußpunkt auf $h$. Der Abstand ist dann $d(g;h)=d(G;H)=\sqrt{(4-(-2))^2+(-10-(-12))^2+(22-19)^2}=\sqrt{36+4+9}=7$.

Die richtigen Zuordnungen sind:

1 und C (Punkt-Ebene)

2 und A(Punkt-Gerade)

3 und B (windschiefe Geraden)

Wenn du hier noch Schwierigkeiten hast, schaue dir den jeweiligen Abschnitt des Lernpfadkapitels an.

Abstand eines Punktes von einer Ebene

Das Lotfußpunktverfahren

Aufgabe 2: Überblick: Abstand Punkt Ebene

Abstand Punkt Ebene

Bei dieser Aufgabe kannst du einen Überblick über die Bestimmung des Abstandes zwischen einem Punkt und einer Ebene mit dem Lotfußpunktverfahren bekommen. Es geht auch um wichtige Begriffe in diesem Zusammenhang.

Fülle die Lücken mit den richtigen Wörtern. Sie werden dir angezeigt, sobald du auf eine Lücke klickst. Wenn du fertig bist, klicke auf den Haken unten rechts.

Die Abbildung kann dir helfen.

Merke: Abstand eines Punktes P zu einer Ebene E - Lotfußpunktverfahren

Das Vorgehen aus Aufgabe 2 hier nochmal detalliert erklärt:

1. Stelle die Gleichung für die zu $E$ orthogonale Gerade $g$ (also die Lotgerade) durch $P$ auf. Dabei kannst du als Stützvektor $\vec{p}$ und als Richtungsvektor den Normalenvektor $\vec{n}$ von $E$ nutzen: $g:\vec{x}=\vec{p}+\vec{t}\cdot\vec{n}$.
2. Bestimme den Schnittpunkt $L$ von der Lotgeraden $g$ und der Ebene $E$. $L$ ist der Lotfußpunkt.
3. Bestimme den Abstand zwischen den Punkten $P$ und $L$, indem du den Betrag des Vektors $\vec{PL}$ berechnest.

Aufgabe 3: Abstände von Punkt-Ebene zuordnen

Berechne die Abstände der verschiedenen Ebenen $E, F, G$ zum Punkt $P(3|4|-2)$. Ordne dann den Ebenen dem jeweiligen Abstand $d$ zu.

Ziehe dazu den passenden Abstand auf die jeweilige Ebene. Möchtest du eine Karte vergrößern, klicke auf die drauf. Klicke am Ende auf den Haken unten rechts, um dich selbst zu überprüfen.

Viel Spaß!

Du kannst auch immer die Hesse´sche Normalenform zur Berechnung benutzten. Im Folgenden wurden die Abstände mit dem Lotfußpunktverfahren berechnet.

Abstand von $E:2x_1+6x_2-4x_3=-32$ und $P(3|4|-2)$:

Die Gleichung für die zu $E:2x_1+6x_2-4x_3=1$ orthogonale Gerade $g$ (also die Lotgerade) durch $P(3|4|-2)$ aufstellen:

$l:\vec{x}=\vec{p}+t\cdot\vec{n}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+t\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}$.

Den Lotfußpunkt $A$ bestimmen:

$E:2(3+2t)+6(4+6t)-4(-2-4t)=32 \Rightarrow t=-1,25$

$t$ in $l$ einsetzten:

$l:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}-1,25\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}=\begin{pmatrix} 0,5 \\ -3,5 \\ 3 \end{pmatrix}$

Der Lotfußpunkt $A$ ist $A(0,5|-3,5|3)$.

Den Abstand zwischen den Punkten $P$ und $A$ bestimmen:

$d(P;A)=|\vec{PA}|=\sqrt((0,5-3)^2+(-3,5-4)^2+(3-(-2))^2)\approx 9,354$

$\Rightarrow d\approx 9,354$

Abstand von $F:\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\cdot(\vec{x}-\begin{pmatrix} 6 \\ -2 \\ 3 \end{pmatrix}) )=0$ und $P(3|4|-2)$:

$F$ in Koordinatenform umschreiben:

$F:\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}\cdot(\vec{x}-\begin{pmatrix} 6 \\ -2 \\ 3 \end{pmatrix})=0 \Leftrightarrow F: x_1+x_2+2x_3=10$

Wenn du hierbei noch Probleme hast, dann schau dir doch nochmal Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum an.

Zu $F$ senkrechte Gerade $m$ durch $P$ aufstellen: $m:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+s\cdot\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$

Koordinaten der Geradengleichung $m$ in $F$ einsetzten:

$F:(3+s)+(4+s)+2(-2+2s)=10 \Leftrightarrow s=\frac{7}{6}$

$m:\vec{x}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+\frac{7}{6}\cdot\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} \frac{25}{6} \\ \frac{31}{6} \\ \frac{1}{3} \end{pmatrix}$

Der Lotfußpunkt $B$ ist $B(\frac{25}{6}|\frac{31}{6}|\frac{1}{3})$.

Den Abstand zwischen den Punkten $P$ und $B$ bestimmen:

$d(P,B)=|\vec{P,B}|=\sqrt((\frac{25}{6}-3)^2+(\frac{31}{6}-4)^2+(\frac{1}{3}-(-2))^2)\approx 2,858$

$\Rightarrow d\approx 2,858$

Abstand von der $x_1x_2-Ebene$ zum Punkt $P(3|4|-2)$:

Sollst du den Abstand eines Punktes zu einer Koordinatenebene bestimmen, so kannst du diesen einfach ablesen und musst ihn nicht berechnen. Der Abstand hier beträgt $2$, da $|-2|$ die $x_3$ Koordinate von $P$ ist und damit den Abstand zur $x_1x_2-Ebene$ anzeigt.

Beachte: ein Abstand ist immer positiv und da $|-2|=2$ ist der Abstand $2$.

$\Rightarrow d=2$

Aufgabe 4: Glaspyramide

a) Im Innenhof des Louvre-Museums in Paris befindet sich eine große Glaspyramide. Die quadratische Grundfläche liegt in einer Ebene, die durch die Ebenengleichung $E: 2x_1+x_2+2x_3=7$ beschrieben werden kann. Die Spitze liegt im Punkt $S(4,5|9|3,5)$. Eine Längeneinheit $LE$ im Koordinatensystem entpricht $4m$.

Welche Höhe hat die Pyramide in $m$?

Mach dir eine Skizze. Welche Teilschritte brauchst du zur Bestimmung des Abstands? Wenn du dir unsicher bist, schau nochmal in die Merkbox oben.

Die Höhe der Pyramide kann man bestimmen, indem man den Abstand zwischen der Spitze $S$ und der Ebene $E$ bestimmt.

Zuerst wird die Geradengleichung der Lotgeraden $g$ zu $E$ durch $P$ aufgestellt. Wir nehmen den Ortsvektor von $S$ als Stützvektor und den Normalenvektor von $E$ als Richtungsvektor, also: $g: \vec{x}= \begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}+ t \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$.

Wir bestimmen den Schnittpunkt von $g$ mit $E$. Einsetzen von einem allgemeinen Punkt von $g$ in $E$ ergibt $(4,5+2t)+(9+t)+2(3,5+2t)=7$, also $t=-2$. Durch Einsetzen in die Geradengleichung $\begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}- 2 \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0,5 \\ 7 \\ -0,5 \end{pmatrix}$ erhalten wir den Lotfußpunkt $L(0,5|7|-0,5)$. Dies ist gleichtzeitig der Mittelpunkt der Grundfläche der Glaspyramide.

Der Abstand zwischen S und L beträgt $6LE$ wegen $|\vec{SL}|=\sqrt{(4,5-0,5)^2+(9-7)^2+(3,5-(-0,5))^2}=6$. Die Pyramide hat also eine Höhe von $24m$.

Die Pyramide hat eine Höhe von $24m$.

Aufgabe 4: Glaspyramide

Spitze der invertierten Glaspyramide

b) An einer anderen Stelle im Innenhof des Louvre befindet sich eine invertierte Glaspyramide. Das bedeutet, ihre quadratische Grundfläche liegt in der gleichen Ebene wie die Grundfläche der großen Glaspyramide, ihre Spitze ist aber unterhalb des Innenhofs. Man kann sie in einem Raum unterhalb des Innenhofs besichtigen. Die Länge der Kante von der Spitze bis zu einer Ecken der Grundfläche beträgt jeweils $10m$. Die Grundfläche hat $12m$ lange Diagonalen, die sich im Punkt $(38 | 1 | -35)$ schneiden. In welchem Punkt $S_2$ liegt die Spitze der umgedrehten Pyramide?

Zeichne eine Skizze, in der du alle bekannten Längenangaben und Punkte einträgst. Was musst du wissen, um die Position der Spitze herauszufinden?

Berechnung der Höhe der Pyramide

Weiter unten findest du eine Skizze der Pyramide, die du mit deiner Maus drehen und vergrößern kannst.

Wenn du die Höhe der Pyramide kennst, weißt du, welchen Abstand die Spitze von der Grundfläche hat. Du kennst auch schon den Mittelpunkt der Pyramiden und kannst entlang des Normalenvektors von $E$ zur Spitze gelangen.

Du kannst die Höhe der Pyramide mithilfe des Satzes von Pythagoras und der Längenangaben berechnen.

Unten siehst du eine Skizze zum Lösungsweg. Die Höhe der Pyramide kann man mit dem Satz des Pythagoras und den Längenangaben für die Diagonale der Grundfläche und die Kanten berechnen: (siehe Zeichnung zu Tipp 2 zu b))

Es ist $\sqrt{10^2-6^2}=\sqrt{64}=8$, also beträgt die Höhe der invertierten Pyramide $8m$, was $2LE$ im Koordinatensystem entspricht.

Die Spitze der umgedrehten Pyramide liegt also in einem Punkt, der einen Abstand von $2LE$ zur Pyramidengrundfläche hat. Es gibt genau zwei solche Punkte, die Spitze einer "normalen" Pyramide und die Spitze der invertierten Pyramide.

Damit man die Spitze der invertierten Pyramide erhält, geht man vom Mittelpunkt $M (38 | 1 | -35)$ der Grundfläche aus $2LE$ entlang der Geraden, die orthogonal zu $E$ ist, und zwar in die andere Richtung als in Aufgabenteil a). Das heißt, man geht $2LE$ in die entgegengesetzte Richung des Normalenvekotrs von $E$.

Es ist $|\vec{n}|=|\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}|=\sqrt{2^2+1^2+2^2}=3$, also ist $\vec{n_0}=\frac{1}{3}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$.

Nun können wir bestimmen, in welchem Punkt $S_2$ die Spitze liegt:

Es ist $\begin{pmatrix} 38 \\ 1 \\ -35 \end{pmatrix}\cdot \frac{1}{3}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} 36 \frac{2}{3} \\ \frac{1}{3} \\ -36 \frac{1}{3} \end{pmatrix}$, also erhält man $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$

Die Spitze der invertierten Pyramide liegt im Punkt $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$.

Die Hesse´sche Normalenform

Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotfußpunktverfahren auch die Möglichkeit, dies mit der Hesse´schen Normalenform zu berechnen. In diesem Abschnitt lernst du, wie du die Normalenform aufstellst und sie zur Abstandsberechnung anwendest.

Merke: Die Hesse´sche Normalenform

Den Abstand von einem Punkt $P$ zu einer Ebene $E$ kann mit einer Formel berechnet werden, der sogenannten Hesse´schen Normalenform (kurz:HNF).

Gegeben ist eine Ebene $E$ durch die Koordinatengleichung $a\cdot x_1+b\cdot x_2+c\cdot x_3=d$ bzw. durch die Normalenform $\vec{n}\cdot\vec{OX}$ mit $\vec{n}= \begin{pmatrix} a \\ b \\ c \end{pmatrix}$ und ein Punkt $P(p_1|p_2|p_3)$.

1. Stelle nun die HNF der Ebene auf: Lies dazu aus der Koordinatengleichung der Ebene den Normalenvektor $\vec{n}= \begin{pmatrix} a \\ b \\ c \end{pmatrix}$ ab.

Bestimme dann die Länge des Normalenvektors $\vec{n}$: $|\vec{n}|=\sqrt{a^2+b^2+c^2}$ .

Die HNF lautet nun: $\frac {|a\cdot x_1+b\cdot x_2+c\cdot x_3-d|}{|\vec{n}|}$.

2. Berechne den Abstand, indem du die Koordinaten des Punktes $P(p_1|p_2|p_3)$ in die HNF einsetzt:

$\frac {|a\cdot p_1+b\cdot p_2+c\cdot p_3-d|}{|\vec{n}|}$

Aufgabe 5:

Über dem Schuldach schwebt eine Drohne an der Stelle $A(3|4|-1)$ und ein Falke schwebt auf der Stelle $B(1|7|4)$. Finde heraus, wer den geringeren Abstand zum Schuldach hat. Das Schuldach lässt sich durch folgende Gleichung beschreiben: $E: 8x_1-4x_2-x_3=5$.

Der Normalenvektor der Ebene ist: $\vec{n}= \begin{pmatrix} 8 \\ -4 \\ -1 \end{pmatrix}$

Länge des Normalenvektors $\vec{n}$ bestimmen: $|\vec{n}|=\sqrt{8^2-4^2+(-1)^2}=\sqrt{64+16+1}=\sqrt{81}=9$

Die HNF lautet nun: $\frac {|8\cdot x_1-4\cdot x_2-1\cdot x_3-5|}{9}$.

Nun werden die Koordinaten von $A$ eingesetzt: $\frac {|8\cdot3-4\cdot4-1\cdot(-1)-5|}{9}=\frac {|24-26+1-5|}{9}=\frac {|-6|}{9}=\frac {6}{9}=\frac {2}{3}$

Die Koordinaten von $B$ können in die selbe HNF eingesetzt werden: $\frac {|8\cdot(-1)-4\cdot7-1\cdot4-5|}{9}=\frac {|-8-28-4-5|}{9}=\frac {|-45|}{9}=5$.

Damit hat die Drohne einen Abstand von $\frac{2}{3}$ zum Schuldach und der Falke einen Abstand von $5$. Die Drohne ist also näher zum Dach als der Vogel.

Der Abstand der Drohne zum Dach beträgt $\frac{2}{3}$ und der Abstand des Falken zum Dach beträgt $5$. Damit ist der Abstand der Drohne geriner.

Aufgabe 6: Abstand paralleler Ebenen

Gegeben ist die Ebene $E: 2x_1-3x_2+6x_3=13$. Bestimme zur Ebene $E$ zwei parallele Ebenen, die von $E$ den Abstand $5$ haben.

Überlege dir, welchen Normalenvektor die Ebenen haben müssen, damit sie parallel zu $E$ sind

Die gesuchten Ebenen haben den gleichen Normalenvektor wie $E$.

Ansatz: $G:2x_1-3x_2+6x_3=h$

$P(p_1|p_2|p_3)$ sei ein Punkt der Ebene $G$.

Es gilt: $d(P;E)=\frac {|2p_1-3p_2+6p_3-13|}{\sqrt{2^2+(-3)^2+6^2}}=\frac{|2p_1-3p_2+6p_3-13|}{\sqrt{49}}=\frac {|2p_1-3p_2+6p_3-13|}{7}=\frac{|h-13|}{7}$.

$d(P;E)=5$ nach Aufgabenstellung. Daher gilt: $\frac{h-13}{7}=5$ oder $\frac{h-13}{7}=-5$.

Stelle nun beide Gleichungen nach $h$ um. Es folgt: $h_1=48$ und $h_2=-22$.

Dies wird nun in die Ebenengleichung von $G$ eingesetzt:

$G_1:2x_1-3x_2+6x_3=48$ $G_2:2x_1-3x_2+6x_3=-22$

$G_1$ und $G_2$ haben nun beide den Abstand $5$ zur Ebene $E$.

$G_1:2x_1-3x_2+6x_3=48$ und $G_2:2x_1-3x_2+6x_3=-22$

haben beide den Abstand $5$ zu $E$.

Falls du noch nicht genug hast, kannst du auch versuchen, die Aufgaben vom Lotfußpunktverfahren mit der Hesse´schen Normalenform zu lösen.

Abstand eines Punktes von einer Geraden

Aufgabe 7: Grafische Darstellung: Abstand eines Punktes von einer Geraden

Bewege den Punkt $Q$ auf der Geraden $g$, um dir den jeweiligen Abstand zwischen den Punkten $P$ und $Q$ anzeigen zu lassen. Rechts neben der Geraden siehst du, wie groß der Abstand jeweils ist.

Wann ist der Abstand vom Punkt $P$ zur Geraden $g$ am kleinsten?

Wie groß ist der Winkel zwischen $g$ und der Geraden durch $P$ und $Q$? Wie nennt man $Q$ dann?

Versuche es zuerst ohne die Hilfslinie. Überprüfe dich dann selbst.

Dies ist der Link zur GeoGebra App, falls die Anzeige bei dir nicht funktioniert:https://www.geogebra.org/material/show/id/cFTUcwnd#

Der Abstand $d(P;Q)=d(P;g)$ ist am kleinsten, wenn $\vec{PQ}$ orthogonal zu $g$ ist. Dies kannst du sehen, wenn du dir die Hilfslinie anzeigen lässt.

Dann nennt man den Punkt $Q$ den Lotfußpunkt von $P$ auf $g$.

Merke: Der Abstand eines Punktes zu einer Geraden

Der Abstand eines Punktes $P$ zu einer Geraden $g$ ist der Abstand von $P$ und $L$, wobei $L$ der Lotfußpunkt von $P$ auf $g$ ist.

Für die Bestimmung des Abstandes $d(P,g)=d(P,G)$ gibt es zwei verschiedene Verfahren:

Verfahren Hilfsebene

1. Stelle eine Hilfsebene $H$ (in Koordinatenform) auf, die den Punkt $P$ enthält und orthogonal zu zu $g$ ist. Dafür kannst du als Stützvektor $\vec{p}$ und als Normalenvektor den Richtungsvektor von $g$ nehmen.
2. Bestimme den Schnittpunkt $L$ von $g$ und $H$ durch Einsetzen.
3. Berechne den Abstand $d(P;g)=d(P;L)$.

Verfahren Orthogonalität

1. Bestimme einen allgmeinen Verbindungsvektor von $P$ zu einem beliebigen Geradenpunkt $L$ in Abhängigkeit vom Geradenparameter $r$.
2. Wähle $r$ so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden $g$ ist.
3. Berechne nun den Abstand $d(P;g)=d(P;L)$.

Aufgabe 8: Lichterkette

Für ein Stadtfest soll von der Spitze $P(-2|3|10)$ eines Restaurants eine Lichterkette auf kürzestem Weg zur nahen Uferlinie des Kanals $g:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+r\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}$ eine Lichterkette gespannt werden. Eine Längeneinheit im Koordinatensystem entspricht $1m$.

Berechne die Mindestlänge der Lichterkette auf Meter gerundet.

1. Stelle die Hilfsebene $H$ in Koordinatenform auf:

$-4x_1+3x_2+2x_3=37, da \begin{pmatrix} -2 \\ 3 \\ 10 \end{pmatrix}\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=37$

2. Schnittpunkt von $g$ und $H$ bestimmen: $-4\cdot(1-4r)+3\cdot(2+3r)+2\cdot(3+2r)=37 \Leftrightarrow -4+16r+6+9r+6+4r=37 \Leftrightarrow 8+29r=37 \Leftrightarrow 29r=29 \Leftrightarrow r=1$

3. $r$ in $g$ einsetzten, um $L$ zu bestimmen:

$g:\vec{x}= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+1\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=\begin{pmatrix} -3 \\ 5 \\ 5 \end{pmatrix}$ $\Rightarrow L(-3|5|5)$

4. Abstand $d(P;L)=d(P;L)$ bestimmen: $d(P;L)=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477$

Die Lichterkette muss mindestens $5,48 Meter$ lang sein.

Die Lichterkette muss mindestens $5,48 Meter$ lang sein.

Aufgabe 9: Die richtige Reihenfolge

Im Folgenden wurde der Abstand von $A(3|9|-2)$ und $g:\vec{x}=\begin{pmatrix} 9 \\ -3 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 4 \\ -5 \\ -7 \end{pmatrix}$ bestimmt. Bringe die einzelnen Schritte in die richtige Reihenfolge.

Aufgabe 10: Dreieck

Es sind die Punkte $B(2|8|1)$ und $C(0,5|3,5|7)$ gegeben, durch sie verläuft die Gerade $g$. Die Strecke $\vec{BC}$ bildet die Grundseite eines Dreiecks mit dem dritten Punkt $A$. $A$ liegt auf der zu $g$ parallelen Geraden $j:\vec{x}= \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}$. a) Stimmt die Behauptung "Der Flächeninhalt des Dreiecks $ABC$ ändert sich, je nachdem wo $A$ auf der Geraden $j$ liegt"? Wenn ja, warum? Wenn nein, warum nicht?

Du kannst mit der Maus den Punkt $A$ verschieben.

Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man $A$ verschiebt?

Die Behauptung stimmt nicht. Den Flächeninhalt $F$ eines Dreiecks kann man bekanntermaßen mit der Formel $F=\frac{1}{2}\cdot G \cdot h$ berechnen, wobei $G$ die Länge der Grundseite ist.

In dieser Aufgabe bleibt der Abstand $d(A;g)$ immer gleich, da sich $A$ auf einer zu $g$ parallelen Geraden "bewegt". Also ist die Höhe $h$ all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt $F=\frac{1}{2}\cdot G \cdot h$ nicht.

b) Bestimme den Flächeninhalt des Dreicks $ABC$.

Überlege dir, welche Abstände du berechnen musst, um den Flächeninhalt bestimmen zu können.

Wir bestimmen zunächst die Länge $G$ der Grundseite: Es $d(B;C)=\sqrt{(2-0,5)^2+(8-3,5)^2+(1-7)^2}=\sqrt{58,5}$.

Nun bestimmen wir die Höhe $h$, also den Abstand der parallelen Geraden $g$ und $j$ mithilfe des Verbindungsvektors von $B$ zur Geraden $j$.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten):

Der Punkt $L_s=(1+t|1+3t|2-4t)$ ist ein allgemeiner Punkt auf $j$. Ein allgemeiner Verbindungsvektor zwischen $B$ und $j$ ist also gegeben durch $\vec{BL_s}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}$.

Damit $\vec{BL_s}$ orthogonal zum Richtungsvektor von $j$ ist, muss gelten: $\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0$ bzw. $(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)$, also $t=1$. Für $L=(2|4|-2)$ ist der Verbindungsvektor also am kürzesten. Somit ist $h=d(B;j)=d(B;L)=\sqrt{(2-2)^2+(4-8)^2+(-2-1)^2}=\sqrt{25}=5$.

Der Flächeninhalt des Dreiecks beträgt also $F=\frac{1}{2}\cdot G \cdot h=\frac{1}{2}\cdot \sqrt(58,5) \cdot 5\approx 19,12$ Flächeneinheiten.

Der Flächeninhalt des Dreiecks beträgt also $19,12$ Flächeneinheiten.

Abstand zweier windschiefer Geraden

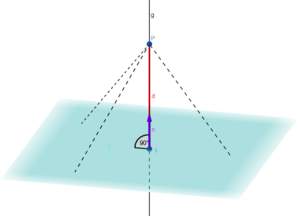
Verschiebe die Punkte $G$ und $H$ so, dass $\overline{GH}$ die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden $g$ und $h$ ist. Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten.

Merke: Der Abstand windschiefer Geraden

Der Abstand zweier windschiefer Geraden $g$ und $h$ ist die kleinste Entfernung zwischen den Punkten von $g$ und den Punkten von $h$. Diese kürzeste Verbindungsstrecke $\overline{GH}$ zwischen den beiden Geraden ist sowohl orthogonal zu $g$ als auch orthogonal zu $h$ und heißt gemeinsames Lot der windschiefen Geraden $g$ und $h$.

Für die Bestimmung des Abstandes $d(g;h)$ berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst: Seien $g: \vec{x}=\vec{p}+s\cdot \vec{u}$ und $h: \vec{x}=\vec{q}+t\cdot \vec{v}$ die windschiefen Geraden.

Verfahren Gemeinsames Lot

1. Bestimme die Geradenpunkte $G$ und $H$ in Abhängigkeit von dem jeweiligen Geradenparameter.
2. Stelle den Verbindungsvektor $\vec{G_s H_t}$ in Abhängigkeit von den Geradenparametern auf.
3. Bestimme nun die Parameter $s$ und $t$ so, dass der Verbindungsvektor $\vec{G_s H_t}$ orthogonal zu den Richtungsvektoren von $g$ und $h$ ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen $\vec{G_s H_t}\cdot \vec{u} =0$ und $\vec{G_s H_t}\cdot \vec{v} =0$.
4. Mit diesen Parametern erhältst du die Lotfußpunkte $G$ und $H$ und kannst den Abstand $d(g;h)=d(G;H)$ bestimmen.

Verfahren Hilfsebene

Es gibt eine Ebene $E$, sodass $g$ in $E$ liegt und $h$ parallel zu $E$ ist. Für diese Ebene $E$ ist dann der Abstand zwischen den Geraden $d(g,h)$ gleich dem Abstand zwischen $E$ und einem beliebigen Punkt $H$ auf $h$. Jeder Normalenvektor von dieser Ebene $E$ ist orthogonal zu den Richtungsvektoren von $g$ und $h$.

1. Bestimme aus den Gleichungen $\vec{u}\cdot\vec{n}=0$ und $\vec{v}\cdot\vec{n}=0$ einen Normalenvektor.
2. Stelle die Normalengleichung $(\vec{x}-\vec{p})\cdot\vec{n}=0$ der Ebene $E$ auf.
3. Bestimme mit der Hesse´schen Normalenform oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand $d(E;H)=d(g;h)$.

Aufgabe 11: Maulwurfstunnel

Zwei Maulwürfe graben Tunnel mit einem Durchmesser von jeweils $5cm$.

Der erste Maulwurf gräbt entlang der Geraden $g:\vec{x}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}$ und der zweite entlang der Geraden $h:\vec{x}=\begin{pmatrix} 6 \\ 6 \\ 18 \end{pmatrix}+t\cdot \begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}$ wobei diese Geraden jeweils in der Mitte des Tunnels liegen.

Die Geraden schneiden sich nicht, aber ihre Tunnel sind nur stabil, wenn sie überall mindestens $15cm$ Erde dazwischen sind. Eine Längeneinheit im Koordinatensystem entspricht $1cm$. Wird das Tunnelsystem halten?

Wenn die kleinste Entfernung, also der Abstand zwischen den Geraden groß genug ist, ist auch an allen anderen Stellen genug Erde zwischen den Tunneln. Überlege dir, welchen Abstand die Geraden voneinander haben müssten, damit die Tunnel nicht einstürzen. Berechne dann den Abstand zwischen den Geraden mit einem Verfahren deiner Wahl.

Da die Tunnel einen Radius von $2,5cm$ haben und die Geraden in dem Modell in der Mitte der jeweiligen Tunnel liegen, müssen die Geraden mindestens einen Abstand von $2,5+15+2,5=20$ haben, damit die Tunnel nicht einstürzen.

Wir bestimmen den Abstand zwischen den Geraden mithilfe einer Hilfsebene $E$, die parallel zur Geraden $h$ ist und in der die Gerade $g$ liegt. Für den Normalenvektor $\vec{n}$ muss gelten: $\begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}\cdot \vec{n}=0$ und $\begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}\cdot \vec{n}=0$. Es folgt $n_1=\frac{2}{3} n_3$ und $n_2=\frac{3}{4} n_3$. Also ist $\vec{n}=\begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix}$ ein Normalenvektor von $E$. Die Normalenform von $E$ lautet nun $E:[\vec{x}-\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}]\cdot \begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix} =0$. Nenne $H=\begin{pmatrix} 6 \\ 6 \\ 18 \end{pmatrix}$. Da der Abstand zwischen den Geraden gleich dem Abstand zwischen der Ebene $E$ und einem beliebigen Punkt auf der zu $E$ parallelen Geraden $h$ ist, erhält man nun mit der Hesse'schen Normalenform $d(g;h)=d(E;H)=\frac{|\frac{2}{3}\cdot 6+\frac{3}{4}\cdot 6+18-(\frac{2}{3}\cdot 1+\frac{3}{4}\cdot 1+1)|}{\sqrt{(\frac{2}{3}^2+(\frac{3}{4})^2+1^2}}=17.$

Die Geraden haben also einen kleineren Abstand als $20LE$. Das heißt, die Tunnel sind nicht überall mindestens $15cm$ voneinander entfernt und sie werden einstürzen.

Die einzige Lösung für die Maulwürfe ist es, an der kritischen Stelle eine gemeinsame Höhle zu bauen. :)

Die Geraden haben einen Abstand von $17LE$. Zwischen den Tunneln sind also an einer Stelle nur $12cm$ Erde und sie werden einstürzen.

Dann bauen die beiden Maulwürfe an der kritischen Stelle einfach eine gemeinsame Höhle. :)

Aufgabe 12

Bei dieser Aufgabe gibt es drei Geradenpaare $g$ und $h$, die jeweils windschief zueinander liegen. Schiebe zuerst die Geradenpaare auf das Feld mit der entsprechenden Nummer. Ordne ihnen dann die jeweiligen Lotfußpunkte $G$ und $H$ sowie den entsprechenden Abstand zwischen den Geraden zu. Ein paar Zettel bleiben übrig, diese schiebst du auf das letzte Feld. Du kannst die Zettel vergrößern, indem du sie anklickst.

Tipp: Durch genaue Überlegungen, Rückwärtsrechnen und mithilfe von Skizzen kann man manchmal schnell erkennen, was zusammengehört, ohne alle Schritte des Verfahrens durchzugehen!

Wenn du auf den Haken klickst, kannst du überprüfen, ob du richtig zugeordnet hast.

Du kannst natürlich auch mit dem Verfahren die beiden Lotfußpunkte bestimmen. Hier kannst du dir aber "rückwärts" schneller überlegen, was die Lotfußpunkte sind: Durch Einsetzen erkennt man, dass $G(0|2|0)$ und $H(-1|0|-2)$ auf der jeweiligen Gerade liegen. Der Verbindungsvektor $\vec{GH}=\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}$ ist wegen $\begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix}\cdot\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}=0$ und $\begin{pmatrix} 1 \\ -\frac{1}{2} \\ 0 \end{pmatrix}\cdot\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}=0$ orthogonal zu $g$ und $h$. Also sind $G(0|2|0)$ und $H(-1|0|-2)$ die Lotfußpunkte und es ist $d(g;h)=|\vec{GH}|=\sqrt{(-1)^2+(-2)^2+(-2)^2}=3$.

Da $g$ entlang der $x_1$-Achse verläuft, liegt diese Gerade auch in der $x_1$-$x_2$-Ebene. Da $h$ parallel zur $x_2$-Achse verläuft und nicht in der $x_1$-$x_2$-Ebene liegt (denn der Eintrag des Stützvektors in der Koordinate $x_3$ ist nicht $0$), ist $h$ parallel zur $x_1$-$x_2$-Ebene. Deshalb haben alle Punkte auf der Geraden $h$ die $x_3$-Koordinate $1$. Also kann man den Abstand der Geraden direkt an der $x_3$-Koordinate des Stützvektors der Geraden $h$ ablesen: $d(g;h)=|1|=1$.

Außerdem liegt $G(0|0|0)$ auf $g$ und $H(0|0|1)$ auf $h$ und der Verbindungsvektor $\vec{GH}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ ist ortoghonal zu den Richtungsvektoren $\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ und $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ beider Geraden. Also sind diese beiden Punkte die Lotfußpunkte. Das gemeinsame Lot liegt außerdem auf der $x_3$-Achse.

Da der Richtungsvektor von $h$ im Eintrag der $x_2$-Koordinate $0$ ist, ist $h$ parallel zur $x_1$-$x_3$-Ebene. $g$ liegt in der $x_1$-$x_3$-Ebene. (Da die Richtungsvektoren von $g$ und $h$ linear unabhängig sind, sind die Geraden nicht parallel zueinander, was aber ja auch schon in der Aufgabenstellung gesagt wurde.) Also kann man den Abstand der Geraden direkt am Unterschied der $x_2$-Koordinaten der Stützvektoren der beiden Geraden ablesen: $d(g;h)=|2-0|=2$. Da man aber nicht genau weiß, wo $g$ liegt (man kennt nur den Richtungsvektor), kann man auch nicht sagen, wo genau die Lotfußpunkte liegen.