Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)

Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Info

In diesem Lernpfadkapitel geht es um die Lagebeziehung zwischen einer Gerade und einer Ebene oder zwischen zwei Ebenen inklusive der Berechnung der Schnittwinkel.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.

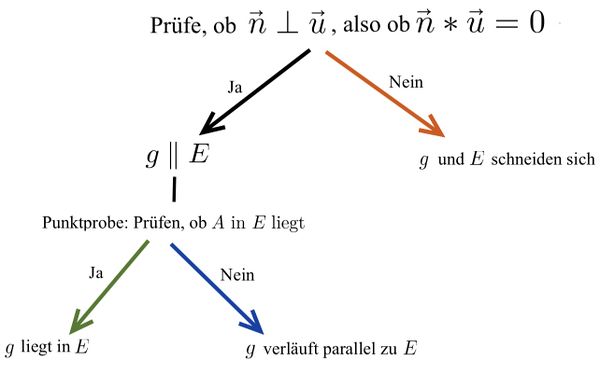
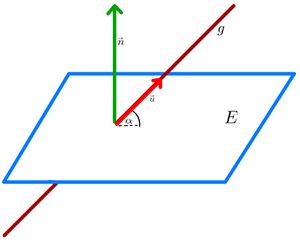
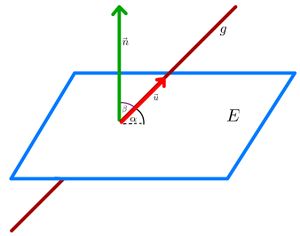
Lagebeziehung Gerade-Ebene

Mögliche Lagebeziehungen zwischen Gerade und Ebene

Merke:

Zwischen einer Geraden und einer Ebene gibt es drei mögliche Lagebeziehungen.

Die Gerade schneidet die Ebene.

Die Gerade und die Ebene liegen parallel.

Die Gerade liegt in der Ebene.

Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Aufgabe 1: Lückentext zur Lagebeziehung zwischen Gerade und Ebene

Vorgehen: Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Beispiel: Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Gegeben sind eine Ebene $E\colon \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right)$ und eine Gerade $g\colon \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right)$. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.

1. Schritt: Setze die Geraden- und Ebenengleichung gleich: $\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right)$

2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf: $\begin{vmatrix} 1-s-t=2-r \\ s=2-4r \\ t=2 \end{vmatrix}$

3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner: $s=-1{,} t=2{,} r=1$

4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen. Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene $E$ und die Gerade $g$ nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.

5. Schritt: Da sich die Ebene $E$ und die Gerade $g$ schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter $r$ in die Geradengleichung ein: $\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ {-}2\\ 2 \end{matrix} \right)$

Alternativ kannst du die Parameter $s$ und $t$ in die Ebenengleichung einsetzen und erhältst den gleichen Punkt.

Aufgabe 2: Untersuchung der Lagebeziehung zwischen Gerade und Ebene

Gegeben ist eine Ebene $E\colon \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right)$. Untersuche die Lagebeziehung zwischen dieser Ebene und den untenstehenden Geraden. Ziehe die Geraden in das entsprechende Feld.

1. Setze die Geradengleichung mit der Ebenengleichung gleich.

2. Stelle ein LGS auf.

3. Löse das LGS mit dem Gaußverfahren oder dem Taschenrechner.

4. Die Anzahl der Lösungen zeigt dir, wie viele gemeinsamen Punkte die Gerade und die Ebene haben. Daran kannst du die Lagebeziehung erkennen.

Aufgabe 3: Schatten eines Sonnensegels

Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind $A = (9|{-}5|7), B= (6|{-}5|7)$ und $C = (7|{-}10|11)$. Die Terrasse wird modelliert durch die $x_1- x_2$-Ebene. Die Sonne scheint aus Richtung $S = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)$. In welchem Bereich hat Frau Meier nun Schatten?

Bestimme die Geraden der Lichtstrahlen durch die Eckpunkte des Sonnensegels und berechne, wo sie auf die Terrasse treffen. Vielleicht hilft dir eine Skizze.

Der Schatten liegt auf der $x_1$-$x_2$-Ebene und du weißt, dass jeder Punkt auf dieser Ebene von der Form: $P = \left( \begin{matrix} x_1\\ x_2\\ 0 \end{matrix} \right)$ ist. Du musst also die Ebenengleichung nicht aufstellen.

1. Schritt: Stelle die Geradengleichungen durch die Eckpunkte des Sonnensegels in Richtung der Sonnenstrahlen auf: $f\colon \vec{x}=\left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)$, $g\colon \vec{x}=\left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)$, $h\colon \vec{x}=\left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right)$

2. Schritt: Berechne die Schnittpunkte der Geraden mit der $x_1-x_2$-Ebene. Da du weißt, dass jeder Punkt in dieser Ebene von der Form $P = \left( \begin{matrix} x_1\\ x_2\\ 0 \end{matrix} \right)$ ist, kannst du diesen Punkt mit der Geradengleichung gleichsetzen.

Berechnung von $A'$:

$\left( \begin{matrix} x_1\\ x_2\\ 0 \end{matrix} \right)=\left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x_1=9-2r \\ x_2=-5-2r \\ 0=7-10r \end{vmatrix} \Rightarrow x_1=\frac{-63}{5}, x_2 = \frac{-32}{5}, r= \frac{7}{10} \Rightarrow A'=\left( \begin{matrix} \frac{-63}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right)$.

Berechnung von $B'$:

$\left( \begin{matrix} x_1\\ x_2\\ 0 \end{matrix} \right)=\left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x_1=6-2s \\ x_2=-5-2s \\ 0=7-10s \end{vmatrix} \Rightarrow x_1=\frac{-42}{5}, x_2 = \frac{-32}{5}, r= \frac{7}{10} \Rightarrow B'=\left( \begin{matrix} \frac{-42}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right)$.

Berechnung von $C'$:

$\left( \begin{matrix} x_1\\ x_2\\ 0 \end{matrix} \right)=\left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x_1=7-2t \\ x_2=-10-2t \\ 0=11-10t \end{vmatrix} \Rightarrow x_1=\frac{-77}{5}, x_2 = \frac{-61}{5}, t= \frac{11}{10} \Rightarrow C'=\left( \begin{matrix} \frac{-77}{5}\\ \frac{-61}{5}\\ 0 \end{matrix} \right)$.

Die Schattenfläche wird also durch das Dreieck mit den Eckpunkten $A'=\left( \begin{matrix} \frac{-63}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right), B'=\left( \begin{matrix} \frac{-42}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right)$ und $C'=\left( \begin{matrix} \frac{-77}{5}\\ \frac{-61}{5}\\ 0 \end{matrix} \right)$ begrenzt.

⭐Merke: Die Lagebeziehung einer Gerade und einer Ebene mit dem Normalenvektor untersuchen

Bei der Bestimmung der Lagebeziehung zwischen einer Gerade $g$ und einer Ebene $E$ kann dir der Normalenvektor der Ebene helfen.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene keinen gemeinsamen Punkt besitzen, so sind sie parallel zueinander.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene orthogonal zueinander sind und Gerade und Ebene unendlich viele gemeinsame Punkte besitzen, so liegt die Gerade in der Ebene.

Wenn der Richtungsvektor der Gerade und der Normalenvektor der Ebene nicht orthogonal zueinander sind, dann schneiden sich die Gerade und die Ebene und es kann ein Schnittpunkt bestimmt werden.

⭐Vorgehen: Untersuchung der Lagebeziehung zwischen Gerade und Ebene mit dem Normalenvektor

⭐ Beispiel: Untersuchung der Lagebeziehung einer Gerade und einer Ebene in Koordinatenform

Gegeben sind eine Ebene $E\colon 2x_1 + x_2 - x_3 = 5$ und eine Gerade $g\colon \vec{x}=\left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right)$. Bestimme die Lagebeziehung von Gerade und Ebene.

1. Schritt: Prüfe, ob der Richtungsvektor der Gerade orthogonal zum Normalenvektor der Ebene liegt: $\vec{n} \ast \vec{u} = \left( \begin{matrix} 2\\ 1\\ {-}1 \end{matrix} \right) \ast \left( \begin{matrix} -3\\ 5\\ {-}1 \end{matrix} \right) = 2 \cdot (-3) + 1 \cdot 5 -1 \cdot (-1) = 0$$\Rightarrow \vec{n} \perp \vec{u}$

2. Schritt: Prüfe durch eine Punktprobe, ob der Stützvektor der Gerade in der Ebene liegt: $2 \cdot 3 -2 =5 \Rightarrow 4 \neq 5$

$\Rightarrow$ Der Stützvektor liegt nicht in der Ebene. Daher verlaufen die Gerade $g$ und die Ebene $E$ parallel zueinander.

⭐ Aufgabe 4: Bestimme den Parameter

Gegeben ist eine Ebene $E\colon \vec{x} = -2x_1 + 3x_2 - x_3 = 3$. Bestimme $l$ und $m$ in den folgenden Geraden so, dass die entsprechende Lagebeziehung erfüllt ist.

a) Die Gerade $g\colon \vec{x} = \left( \begin{matrix} 5\\ 3\\ 0 \end{matrix} \right) + r \cdot \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right)$ soll parallel zur Ebene $E$ verlaufen.

Damit die Gerade $g$ und die Ebene $E$ parallel zueinander sind, müssen der Richtungsvektor von $g$ und der Normalenvektor von $E$ orthogonal zueinander sein.

$\vec{u} \ast \vec{n} = \left( \begin{matrix} \frac{1}{2}\\ 3\\ m \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 8-m$.

Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt $0$ sein: $8-m = 0 \Rightarrow m = 8$.

b) Die Gerade $h\colon \vec{x} = \left( \begin{matrix} l\\\frac{51}{10}\\ \frac{2}{5} \end{matrix} \right) + s \cdot \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right)$ soll in der Ebene $E$ liegen.

Damit die Gerade $g$ in der Ebene $E$ liegt, müssen der Richtungsvektor von $g$ und der Normalenvektor von $E$ orthogonal zueinander sein.

Wenn die Gerade $g$ in der Ebene $E$ liegt, liegt jeder Punkt auf der Gerade $g$ auch in der Ebene $E$. Prüfe mit der Punktprobe, ob der Stützvektor von $g$ in der Ebene $E$ liegt.

Finde zuerst m: $vec{u} \ast \vec{n} = \left( \begin{matrix} 3\\ m\\ \frac{18}{5} \end{matrix} \right) \ast \left( \begin{matrix} -2\\ 3\\ {-}1 \end{matrix} \right) = 3m - \frac{48}{5}$. Damit die beiden Vektoren orthogonal zueinander sind, muss das Skalarprodukt $0$ sein: $3m - \frac{48}{5} = 0 \Rightarrow m = \frac{16}{5}$.

Finde danach $l$ durch eine Punktprobe: Setze $\vec{a} = \left( \begin{matrix} l\\ \frac{51}{10}\\ \frac{2}{5} \end{matrix} \right)$ in die Ebenengleichung ein und löse nach l auf: $-2l + 3 \cdot \frac{51}{10} - \frac{2}{5}= 3 \Leftrightarrow l = \frac{119}{20}$.

c) Die Gerade $i\colon \vec{x} = \left( \begin{matrix} 3\\ 0\\ 2 \end{matrix} \right) + t \cdot \left( \begin{matrix} m\\ 5\\ {-}1 \end{matrix} \right)$ soll die Ebene $E$ schneiden.

Es gibt keine eindeutige Lösung! Der Richtungsvektor $\vec{u}$ von $g$ darf nur nicht orthogonal zum Normalenvektor von $E$ liegen.

Für $m = 8$ ist der Richtungsvektor von $g$ orthogonal zum Normalenvektor von $E$ und die Gerade $g$ liegt parallel zur Ebene $E$. Jeder andere Wert für $m$ ist eine richtige Lösung.

⭐ Aufgabe 5: Beamer

Luca hält einen Vortrag vor seiner Klasse. Mit einem Laserpointer möchte er auf einer Karte an der Wand etwas zeigen. Die Wand des Klassenraums wird durch die Ebene $E\colon x_2 + 3x_3 = 2$ dargestellt. Der Strahl des Laserpointers wird durch die Gerade $j\colon \vec{x} = \left( \begin{matrix} {-}5\\ 1 \frac{3}{2} \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ 2\\ \frac{1}{2} \end{matrix} \right)$ modelliert. Berechne ohne Taschenrechner, wo der Strahl aus Lucas Laserpointer auf die Karte an der Wand trifft.

Berechne den Schnittpunkt der Gerade mit der Ebene, indem du die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.

Setze die einzelnen Koordinaten der Gerade in die Ebenengleichung ein: $-5 + 2s + 3(\frac{3}{2} + \frac{1}{2}s) = 2 \Leftrightarrow s \approx 0{,}71$

Berechne den Schnittpunkt, indem du $s$ in die Geradengleichung einsetzt: $\left( \begin{matrix} 7\\ {-}5\\ \frac{3}{2} \end{matrix} \right) + 0{,}71 \cdot \left( \begin{matrix} 1\\ 2\\ \frac{1}{2} \end{matrix} \right) = \left( \begin{matrix} 7{,}71\\ {-}3{,}58\\ 1{,}86 \end{matrix} \right)$

⭐Berechnung des Winkels zwischen Gerade und Ebene

Merke: Berechnung des Winkels zwischen Gerade und Ebene

Wenn eine Gerade $g$ eine Ebene $E$ schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum

Merksatz: Winkel berechnen zwischen Gerade und Ebene

Abbildung: Winkel zwischen Gerade und Ebene

Sei $E$ eine Ebene mit dem Normalenvektor $\vec{n}$ und $g$ eine Gerade mit dem Richtungsvektor $\vec{u}$. Der Schnittwinkel $\alpha$ zwischen $E$ und $g$ kann mit folgender Formel berechnet werden: $\sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}$.

Ist nach dem Schnittwinkel gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. Dein berechneter Winkel $\alpha$ darf also nur zwischen $0^{\circ}$ und $90^{\circ}$ liegen. Ist dein berechneter Winkel $\alpha > 90^{\circ}$, so musst du $180^{\circ} - \alpha$ berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen.

Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen:

Abbildung: Winkel zwischen Gerade und Ebene

Der Normalenvektor $\vec{n}$ einer Ebene steht in einem $90^{\circ}$ Winkel zur Ebene $E$.

Wenn man den Winkel zwischen einer Gerade $g$ und einer Ebene $E$ berechnen will, kann wie beim Winkel zwischen zwei Geraden mit der Kosinusfunktion der Winkel zwischen dem Richtungsvektor von $g$ und dem Normalenvektor von $E$ berechnet werden. In der Abbildung ist dieser Winkel mit $\beta$ bezeichnet. Um nun den Winkel $\alpha$ zwischen $g$ und $E$ zu erhalten, müssen wir $\beta$ von $90^\circ$ abziehen. Dies entspricht aufgrund trigonometrischer Gesetzmäßigkeiten der obigen Formel mit der Sinusfunktion.

Beispiel: Berechnung des Winkels zwischen Gerade und Ebene

Gegeben sind die Gerade $g\colon \vec{x}=\left( \begin{matrix} {-}1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)$ und die Ebene $E\colon 2x_1 + x_2 + 4 x_3 = {-}27$. Bestimme den Winkel, unter dem sich die Gerade $g$ und die Ebene $E$ schneiden.

1. Schritt: Notiere den Richtungvektor $\vec{u}$ der Gerade und den Normalenvektor $\vec{n}$ der Ebene.

$\vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right)$ und $\vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right)$

2. Schritt: Setze die Vektoren in die Formel $\sin(\alpha)=\frac{ \vec{n} \ast \vec{u}}{|\vec{n}| \cdot |\vec{u}|}$ ein. $\sin(\alpha)=\frac{ \left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \ast \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|} \Leftrightarrow \sin(\alpha)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow \sin(\alpha)=\frac{18}{\sqrt{1260}}$

3. Schritt: Forme die Gleichung um.

$\alpha = sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \alpha \approx 28{,}45^{\circ}$

Der Winkel beträgt also $28{,}45^{\circ}$.

Aufgabe 6: Trinkpäckchen

Abbildung Trinkpäckchen

Eine Schulklasse nimmt auf ihrem Wandertag viele Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Berechne den Winkel, in dem die Kinder den Strohhalm halten müssen, um auch an den Saft in der letzten Ecke zu kommen. Jedes Trinkpäckchen hat die Form eines Quaders (siehe Abbildung). Die Seite, auf der sich das Loch für den Strohhalm befindet, kann durch die Ebene $F\colon x_1=5$ beschrieben werden.

Wenn der Strohhalm so in das Trinkpäckchen gesteckt wird, das er in der hintersten Ecke anstößt, kann er durch die Gerade $g$ veranschaulicht werden: $g\colon \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix}$.

Vielleicht hilft dir die Skizze.

Gesucht wird der Winkel zwischen der Gerade $g$ und der Ebene $F$. Der Richtungsvektor der Gerade ist $\vec{u} = \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix}$. Der Normalenvektor der Ebene kann abgelesen werden: $\vec{n} = \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}$.

Einsetzen der Vektoren in die Formel liefert:

$\sin(\alpha)=\frac{ \left| \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix} \ast \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|} \Leftrightarrow \sin(\alpha)=\frac{5}{\sqrt{1} \cdot \sqrt{25+36+121}} \Leftrightarrow \sin(\alpha)=\frac{1}{\sqrt{182}}$

Mithilfe des Taschenrechners kann das Ergebnis berechnet werden:

$\alpha = sin^{-1}(\frac{1}{\sqrt{182}}) \Leftrightarrow \alpha \approx 21{,}75^{\circ}$

Die Kinder sollten den Strohhalm also in einem Winkel von ca. $21{,}75^{\circ}$ in das Trinkpäckchen stecken, um an den Saft in der letzten Ecke zu kommen.

Aufgabe 7: Gerade gesucht

Eine Gerade $g$ soll die $x_1$-$x_2$-Ebene in einem Winkel von $45^{\circ}$ schneiden. Über die Gerade $g$ ist nur bekannt, dass sie im Punkt $P (1|2|3)$ beginnt und sie in Richtung des Vektors $\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}$ verläuft. Stelle die Gerade $g$ auf.

Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?

Der Normalenvektor der $x_1$-$x_2$ -Ebene verläuft nur in $x_3$-Richtung.

Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.

Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen.

Bestimme dafür zuerst den Normalenvektor der Ebene. Da es sich um die $x_1-x_2$ -Ebene handelt, lautet der Normalenvektor $\vec{n}=\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}$.

Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel eingesetzt werden: $\sin(45)=\frac{ \left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|} \Leftrightarrow \sin(45)=\frac{z}{\sqrt{1} \cdot \sqrt{9+36 + z^{2}}} \Leftrightarrow \sin(45)=\frac{z}{\sqrt{45+z^{2}}}$

Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: $z=3 \sqrt{5} \approx 6{,}71$.

Somit kann im letzten Schritt die Gerade $g$ aufgestellt werden. Man erhält $g\colon \vec{x} = \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 3\\ 6\\ {3 \sqrt{5}} \end{matrix} \right)$.

Lagebeziehung Ebene-Ebene

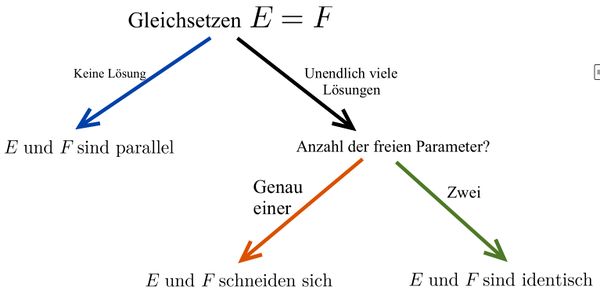
Mögliche Lagebeziehungen zwischen zwei Ebenen

Merke:

Zwischen zwei Ebenen gibt es drei mögliche Lagebeziehungen:

Die Ebenen schneiden sich in einer Schnittgeraden.

Die Ebenen sind parallel.

Die Ebenen sind identisch.

Aufgabe 8: Lückentext zur Lagebeziehung zwischen Ebene und Ebene

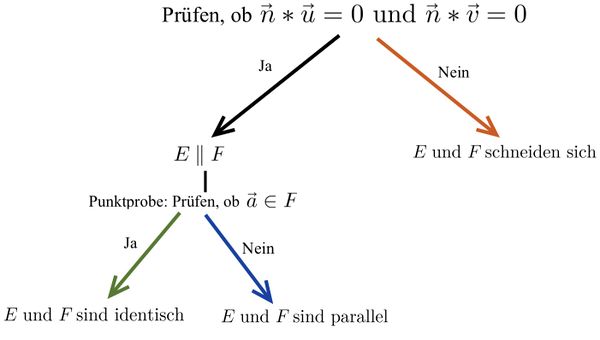
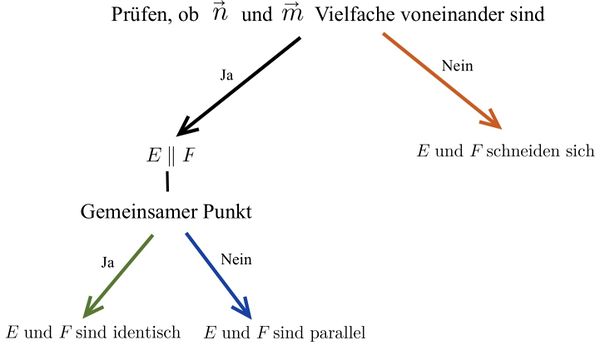
Untersuchung der Lagebeziehung von zwei Ebenen

Beide Ebenengleichungen in Parameterform

Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen.

Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform

Gegeben sind eine Ebene $E\colon \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right)$ und eine Ebene $F\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)$. Untersuche die Lagebeziehung der beiden Ebenen.

1. Schritt: Setze die beiden Ebenengleichungen gleich.

$\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right)= \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)$

2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf.

$\begin{vmatrix} 1+k+3l=1+2r+5s \\ 4-2k+l=2+3r+4s \\ k-l=3-2r-3s \end{vmatrix} \Leftrightarrow \begin{vmatrix} -k+3l-2r+5s=0 \\ {-}2k+l-3r-4s=-2 \\ k-l+2r+3s=3 \end{vmatrix}$

3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner:

$\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13\end{vmatrix}$

4. Schritt: Interpretiere die Lösung des Gleichungssystems:

In der dritten Zeile der Lösungsmatrix befindet sich ein Widerspruch. Somit hat das LGS keine Lösung und die beiden Ebenen sind parallel.

Aufgabe 9: Ergebnisse interpretieren

Interpretiere die jeweilige Situation geometrisch.

a) $\begin{vmatrix} 1 & 0 & 0 & -0{,}5 & 0{,}5 \\ 0 & 1 & 0 & -1 & 0{,}5 \\ 0 & 0 & 1 & 1{,}5 & 1 \end{vmatrix}$

Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, ist nur ein Parameter frei wählbar und die Ebenen schneiden sich in einer Schnittgeraden.

b) $\begin{vmatrix} 1 & 0 & -1 & -1 & 2 \\ 0 & 1 & -1 & -3 & -5 \\ 0 & 0 & 0 & 0 & -5 \end{vmatrix}$

Das Gleichungssystem besitzt keine Lösung, da sich in der dritten Zeile ein Widerspruch befindet. Die Ebenen liegen also parallel zueinander.

c) $\begin{vmatrix} 1 & 3 & -2 & -5 & 3 \\ 0 & 7 & -7 & 14 & 7 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}$

Das Gleichungssystem besitzt unendlich viele Lösungen. Da die dritte Zeile nur aus Nullen besteht, sind zwei Parameter frei wählbar und die Ebenen identisch.

⭐Ebenengleichungen in Parameter- und Koordinatenform

Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen.

Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform

Gegeben sind eine Ebene $E\colon \vec{x}=\left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)$ und eine Ebene $F\colon -1{,}5x_1+3x_2-1{,}5x_3=4{,}5$. Untersuche die Lagebeziehung der beiden Ebenen.

1. Schritt: Prüfe, ob die Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ orthogonal zum Normalenvektor $\vec{v}$ der Ebene $F$ liegen.

Hierfür muss gelten, dass $\vec{n} \ast \vec{u}=0$ und $\vec{n} \ast \vec{v}=0$.

$\vec{n} \ast \vec{u}=\left( \begin{matrix} {-}1{,}5\\ 3\\ {-}1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right)=-1{,}5+0+1{,}5=0$

$\vec{n} \ast \vec{v}=\left( \begin{matrix} -1{,}5\\ 3\\ {-}1{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right)=-3+3+0=0$

2.Schritt: Interpretiere die Lösung des Skalarproduktes:

Da das Skalarprodukt der Vektoren $0$ ist, liegen sie orthogonal zueinander. Das bedeutet, dass die Ebenen sich nicht in einer Schnittgeraden schneiden, sondern entweder identisch oder parallel sind.

3. Schritt: Überprüfe die Lagebeziehung mithilfe der Punktprobe.

Setze hierfür den Stützvektor (Aufpunkt) der Ebene $E$ in die Ebenengleichung der Ebene $F$ ein.

$-1{,}5\cdot2+3\cdot1-1{,}5\cdot(-3)=4{,}5\Leftrightarrow4{,}5=4{,}5$

4. Schritt: Interpretiere die Lösung der Punktprobe.

Da der Aufpunkt die Koordinatengleichung von $F$ erfüllt, liegt $E$ in $F$ und die Ebenen sind identisch.

Aufgabe 10: Lagebeziehungen berechnen

Untersuche die Lagebeziehung der jeweiligen Ebenen.

a) $E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 0 \\ {-}1 \\ 2 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$

$F\colon 7x_1+x_2-3x_3-8=0$

Prüfe, ob die Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ orthogonal zum Normalenvektor $\vec{v}$ der Ebene $F$ liegen.

$\vec{n} \ast \vec{u}=\left( \begin{matrix} 0\\ {-}1\\ 2 \end{matrix} \right)\ast\left( \begin{matrix} 7\\ 1\\ {-}3 \end{matrix} \right)=-7$

$\vec{n} \ast \vec{v}=\left( \begin{matrix} 1\\ 0\\ 0\end{matrix} \right)\ast\left( \begin{matrix} 7\\ 1\\ {-}3 \end{matrix} \right)=7$

Da das Skalarprodukt der Vektoren $\neq0$ ist, liegen sie nicht orthogonal zueinander. Somit schneiden sich die Ebenen in einer Schnittgeraden.

b) $E\colon \vec{x} = \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix}+ s \cdot \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix}$

$F\colon -3x_1-9x_2-x_3=5$

Prüfe, ob die Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ orthogonal zum Normalenvektor $\vec{v}$ der Ebene $F$ liegen.

$\vec{n} \ast \vec{u}=\left( \begin{matrix} 2\\ {-}1\\ 3 \end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0$

$\vec{n} \ast \vec{v}=\left( \begin{matrix} {-}1\\ 0\\ 3\end{matrix} \right)\ast\left( \begin{matrix} {-}3\\ {-}9\\ {-}1 \end{matrix} \right)=0$

Da das Skalarprodukt der Vektoren $0$ ist, liegen sie orthogonal zueinander.

Punktprobe:$-3\cdot{-}3-9\cdot1-0=-18\neq5$

Da die Koordinatengleichung $F$ nicht erfüllt wird, liegen die Ebenen parallel zueinander.

c) $E\colon \vec{x} = \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ {-}0{,}5 \end{pmatrix}+ s \cdot \begin{pmatrix} 4 \\ 2 \\ 1 \end{pmatrix}$

$F\colon 2x_1-2x_2-4x_3=-6$

Prüfe, ob die Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ orthogonal zum Normalenvektor $\vec{v}$ der Ebene $F$ liegen.

$\vec{n} \ast \vec{u}=\left( \begin{matrix} -1 \\ 0 \\ {-}0{,}5 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0$

$\vec{n} \ast \vec{v}=\left( \begin{matrix} 4 \\ 2 \\ 1 \end{matrix} \right)\ast\left( \begin{matrix} 2\\ {-}2\\ {-}4 \end{matrix} \right)=0$

Da das Skalarprodukt der Vektoren $0$ ist, liegen sie orthogonal zueinander.

Punktprobe:$2\cdot2-2\cdot(-1)-3\cdot4=-6\Leftrightarrow-6=-6$

Da die Koordinatengleichung von $F$ erfüllt wird, liegt $E$ in $F$ und die Ebenen sind identisch.

⭐Beide Ebenengleichungen in Koordinatenform

Merke: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform

Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform

Gegeben sind eine Ebene $E\colon 3x_1-4x_2-x_3=4$ und eine Ebene $F\colon 3x_1-3x_2+x_3=3$. Untersuche die Lagebeziehung der beiden Ebenen.

1. Schritt: Prüfe, ob der Normalenvektor $\vec{n}$ der Ebene $E$ ein Vielfaches des Normalenvektors $\vec{m}$ der Ebene $F$ ist.

$r\cdot\vec{n}=\vec{m} \Leftrightarrow r\cdot\left( \begin{matrix} 3\\ {-}4\\ {-}1 \end{matrix} \right)=\left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) \Leftrightarrow \begin{vmatrix} 3r=1\\ {-}4r=0 \\ {-}r=-1 \end{vmatrix}$

2. Schritt: Interpretiere die Lösung des LGS.

Da das LGS nicht lösbar ist, sind die beiden Gleichungen linear unabhängig und die Ebenen schneiden sich in einer Schnittgeraden.

3. Schritt: Bestimme die Schnittgerade.

Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algorithmus oder dem Taschenrechner.

$\begin{vmatrix} 3 & -4 & -1 & 4 \\ 3 & -3 & 1 & 3 \end{vmatrix} \Leftrightarrow \begin{vmatrix} 3 & -4 & -1 & 4 \\ 0 & 1 & 2 & -1 \end{vmatrix}$

Setze $x_3=t$ und bestimme $x_1$ und $x_2$.

$x_2=-1-2t$

$x_1=-\frac{7}{3}$

Stelle die Geradengleichung auf.

$g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix}$

Aufgabe 11: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform

Gegeben ist eine Ebene $E\colon \vec{x}=-2x_1-3x_2+x_3=2$. Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld.

Um die Lagebeziehung von zwei Ebenen in Koordinatenform zu bestimmen, benötigst du keinen Taschenrechner.

Vergleiche die Gleichungen der zwei Ebenen miteinander. Die Ebenen schneiden sich, wenn die beiden Gleichungen linear unabhängig voneinander sind. Die Ebenen sind parallel, wenn die Normalenvektoren identisch oder Vielfache voneinander sind, aber das LGS keine Lösung besitzt.

DIe Ebenen sind identisch, wenn die Normalenvektoren identisch oder Vielfache voneinander sind und das LGS somit unendlich viele Lösungen hat.

Aufgabe 12: Schnitt von zwei Zeltflächen

Die beiden Seitenflächen eines Zeltes liegen in den Ebenen $E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}$ und $F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}$. Der Erdboden wird durch die $x_1$-$x_2$ -Ebene aufgespannt. In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem $50$ cm entspricht?

Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.

Die obere Zeltkante entspricht der Schnittgeraden der beiden Ebenen.

Die Höhe der Zeltkante kannst du mithilfe des Stützvektors der Schnittgeraden ermitteln.

Die Zeltkante entspricht der Schnittgeraden der beiden Ebenen. Um die Höhe zu bestimmen, benötigt man also den Stützvektor der Geradengleichung der Zeltkante.

Da die Ebenen in Parameterform gegeben sind, setzen wir die Gleichungen zunächst gleich und lösen dann das entsprechende LGS:

$\begin{vmatrix} 8-r=8-t \\ 3s=6-3u \\ 4s=4u \end{vmatrix} \Leftrightarrow \begin{vmatrix} -r+t=0\\ 3s+3u=6 \\4s-4u=0 \end{vmatrix}$

$\Rightarrow \begin{vmatrix} -1 & 0 & 1 & 0 & 0 \\ 0 & 3 & 0 & 3 & 6 \\ 4 & 0 & 0 & 4 & 0\end{vmatrix}$

$\Rightarrow s=u=1$ und $r=t$

Einsetzen von $s$ in $E$ ergibt:

$E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ 1 \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}$

Die Schnittgerade der beiden Ebenen lautet demnach:

$g\colon \vec{x} = \left( \begin{matrix} 8\\ 3\\ 4 \end{matrix} \right) + v \cdot \left( \begin{matrix} -1\\ 0\\ 0 \end{matrix} \right)$

Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der $x_3$-Koordinate des Vektors bestimmt werden.

Die obere Zeltkante befindet sich also in $2$ m Höhe.

⭐Berechnung des Winkels zwischen Ebene und Ebene

Merke: Berechnung des Winkel zwischen zwei Ebenen

Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.

Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum.

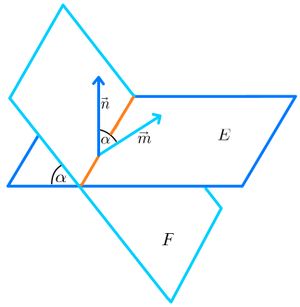
Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen

Abbildung: Winkel zwischen zwei Ebenen

Seien $E$ und $F$ zwei sich schneidende Ebenen mit den Normalenvektoren $\vec{n}$ und $\vec{m}$. Der Schnittwinkel $\alpha$ zwischen $E$ und $F$ kann mit folgender Formel berechnet werden: $\cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}$.

Ist nach dem Schnittwinkel gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von den Ebenen eingeschlossen werden. Dein berechneter Winkel $\alpha$ darf also nur zwischen $0^{\circ}$ und $90^{\circ}$ liegen. Ist dein berechneter Winkel $\alpha > 90^{\circ}$, so musst du $180^{\circ} - \alpha$ berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen.

Beispiel: Winkel berechnen zwischen zwei Ebenen

Gegeben sind zwei Ebenen $E$ und $F$ mit $E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}$ und $F\colon 7x_1+x_2-3x_3$. Berechne den Schnittpunkt zwischen den Ebenen.

1. Schritt: Bestimmte die Normalenvektoren von $E$ und $F$.

Der Normalenvektor von $E$ ist $\vec{n} = \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix}$ . Der Normalenvektor von $F$ lautet $\vec{m} = \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}$.

2. Schritt: Einsetzen der Normalenvektoren in die Formel.

$\cos(\alpha)=\frac{\left| \begin{pmatrix} 2\\ {-}2\\ {-}1 \end{pmatrix} \ast \begin{pmatrix} 7\\ 1\\ {-}3 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ {-}2\\ {-}1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 7\\ 1\\ {-}3 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{16}{\sqrt{9} \cdot \sqrt{59}} \Leftrightarrow \cos(\alpha) = \frac{16}{3 \cdot \sqrt{59}}$

3. Schritt: Auflösen der Gleichung.

$\alpha = cos^{-1}(\frac{16}{3 \cdot \sqrt {59}}) \Leftrightarrow \alpha \approx 46{,}03^{\circ}$ Der Winkel zwischen den Ebenen $E$ und $F$ beträgt ca. $46{,}03^{\circ}$.

Aufgabe 13: Schnittwinkel zwischen Ebenen

Sei $E$ eine Ebene mit $E\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix}$ , $F$ eine Ebene mit $F\colon 2x_1+6x_2-4x_3=2$. und $H$ eine Ebene mit $H\colon 2x_1+4x_2-7x_3=13$ .

Berechne den Winkel zwischen

a) E und F

Bei der Ebene $E$ handelt es sich um die $x_1-x_2-$ Ebene. Der Normalenvektor ist also $\vec{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$. Der Normalenvektor der Ebene $F$ kann abgelesen werden: $\vec{m} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix}$.

Einsetzen in die Formel liefert:

$\cos(\alpha) = \frac{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 2\\ 6\\ 4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2\\ 6\\ 4 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{|4|}{\sqrt{1} \cdot \sqrt{4+36+16}} \Leftrightarrow \cos(\alpha) = \frac{4}{\sqrt{56}}$

Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:

$\alpha = cos^{-1}(\frac{4}{\sqrt {56}}) \Leftrightarrow \alpha \approx 57{,}69^{\circ}$ Der Winkel zwischen den Ebenen $E$ und $F$ beträgt ca. $57{,}69^{\circ}$.

b) F und H und

Die Normalenvektor der Ebenen $F$ und $H$ können abgelesen werden als $\vec{m} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix}$ und $\vec{l} = \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix}$

Einsetzen in die Formel liefert:

$\cos(\alpha) = \frac{ \left| \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{0}{\sqrt{4+36+16} \cdot \sqrt{4+16+49}} \Leftrightarrow \cos(\alpha) = \frac{0}{\sqrt{3864}} \Leftrightarrow \cos(\alpha) = 0$.

Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:

$\alpha = cos^{-1}(0) \Leftrightarrow \alpha = 90^{\circ}$ Der Winkel zwischen den Ebenen $F$ und $H$ beträgt ca. $90^{\circ}$.

c) E und H.

Bei der Ebene $E$ handelt es sich um die $x_1-x_2-$ Ebene. Der Normalenvektor ist also $\vec{n} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$. Der Normalenvektor der Ebene $H$ kann abgelesen werden: $\vec{m} = \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix}$.

Einsetzen in die Formel liefert:

$\cos(\alpha) = \frac{\left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \ast \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right| }{\left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} \right|} \Leftrightarrow \cos(\alpha) = \frac{|{-}7|}{\sqrt{1} \cdot \sqrt{4+16+49}} \Leftrightarrow \cos(\alpha) = \frac{7}{\sqrt{69}}$

Nun muss die Formel mit Hilfe des Taschenrechners aufgelöst werden:

$\alpha = cos^{-1}(\frac{7}{\sqrt {69}}) \Leftrightarrow \alpha \approx 32{,}57^{\circ}$ Der Winkel zwischen den Ebenen $E$ und $H$ beträgt ca. $32{,}57^{\circ}$.

Aufgabe 14: Ebenen gesucht

Der Winkel zwischen den beiden Vektoren $\vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}$ beträgt $67{,}62^{\circ}$.

Gib die Gleichungen zweier Ebenen $E$ und $F$ an, die sich in einem Winkel von $67{,}62^{\circ}$ schneiden.

Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen ihren Normalenvektoren. Da der Winkel zwischen den beiden angebenen Vektoren $\vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}$ und $\vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}$ genau dem Winkel entspricht, den die Ebenen einschließen sollen, können sie als Normalenvektoren der Ebenen verwendet werden. Die Punkte, durch die die Ebenen laufen, können frei gewählt werden.

Eine mögliche Lösung für die Ebenen lautet daher:

$E\colon x_1 + 3x_3 = 4$ und $F\colon 4x_1 + 7x_2 + 2x_3 = 8$.

Aufgabe 15: Bank am Wanderweg

An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene $S_1\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0{,}5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0{,}4 \\ 0\end{pmatrix}, r,s \in [0, 1]$ und die Rückenlehne durch die Ebene $R_1\colon -x_2 + 0{,}4 x_3 = -0{,}2$ beschrieben werden kann.

a) Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen $100^{\circ}$ und $110^{\circ}$ liegen. Überprüfe, ob dies auf die neue Bank zutrifft.

Mache dir eine Skizze. Überlege genau, welchen Winkel du berechnen musst.

Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank

Als Normalenvektor der Ebene $S_1$ erhält man $\vec{n}=\begin{pmatrix} 0 \\ 0 \\ 0{,}8 \end{pmatrix}$ und als Normalenvektor der Ebene $R_1$ $\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}$ .

Einsetzen in die Formel liefert:

$\cos(\gamma)=\frac{\left| \begin{pmatrix} 0\\ 0\\ 0{,}8 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 0{,}8 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\gamma) = \frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}}$

Umstellen der Formel ergibt: $\gamma=cos^{-1} \left( \frac{\frac{8}{25}}{\frac{4}{5} \cdot \sqrt{\frac{29}{25}}} \right) \Leftrightarrow \gamma \approx 68{,}2^{\circ}$

Wie in der Abbildung zu sehen wurde der Winkel $\gamma$ berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel $\alpha$ beschrieben. $\alpha$ erhält man, indem man $180^\circ - \gamma$ berechnet: $180^{\circ} - 68{,}2^{\circ} = 111{,}8^{\circ}$. Mit einem Wert von $111{,}8^{\circ}$ liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel.

b)

Skizze: Bänke am Wanderweg

Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene $S_2\colon \vec{x} = \begin{pmatrix} 0 \\ 0{,}8 \\ 0{,}5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0{,}4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}$ und die Rückenlehne der Ebene $R_2\colon -x_2 - 0{,}4 x_3 = -1$ Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen.

Skizze: Winkel zwischen den beiden Bänken am Wanderweg

Gesucht ist der Winkel zwischen der Ebene $R_1$ und der Ebene $R_2$. Nutze zur Berechnung die Normalenvektoren der Ebenen.

Es soll der Winkel zwischen den beiden Rückenlehnen $R_1$ und $R_2$ berechnet werden.

Die Normalenvektoren der Ebenen lauten $\vec{m}=\begin{pmatrix} 0 \\ -1 \\ 0{,}4 \end{pmatrix}$ und $\vec{l}=\begin{pmatrix} 0 \\ -1 \\ -0{,}4 \end{pmatrix}$.

Einsetzen in die Formel liefert:

$\cos(\beta)=\frac{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \ast \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ {-}1\\ 0{,}4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0\\ {-}1\\ {-}0{,}4 \end{pmatrix} \right|} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\sqrt{\frac{29}{25}} \cdot \sqrt{\frac{29}{25}}} \Leftrightarrow \cos(\beta)=\frac{\frac{21}{25}}{\frac{29}{25}} \Leftrightarrow \cos(\beta)=\frac{21}{29}$

Umstellen der Formel ergibt: $\beta=cos^{-1} \left( \frac{21}{29} \right) \Leftrightarrow \beta \approx 43{,}6^{\circ}$. Der Winkel zwischen den beiden Rückenlehnen beträgt $43{,}6^{\circ}$.

zurück zur Kapitelauswahl