Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum

Info

In diesem Lernpfadkapitel werden Ebenen im Raum eingeführt. Neben Punkten, Vektoren und Geraden sind auch Ebenen wichtige Objekte der analytischen Geometrie.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Die Parameterform und die Punktprobe

Merksatz: Die Parameterform

Eine Ebene $E$ ist bestimmt durch einen Punkt A und zwei Vektoren $\vec {u} \neq 0$ und $\vec{v} \neq 0$, die nicht parallel zueinander sind.

Diese Ebene $E$ kann wie folgt beschrieben werden: $E:\vec{x}=\vec{OA}+s \cdot \vec{u} +t\cdot \vec{v}$

Diese Vektorgleichung bezeichnet man als Parameterdarstellung/Parametergleichung der Ebene $E$ mit den Parameter $s$ und $t$.

Um eine Parameterdarstellung aufzustellen reichen, statt eines Punktes und zwei Vektoren, auch:

• drei Punkte, die nicht alle auf einer Geraden liegen
• Gerade und Punkt
• zwei sich schneidende Geraden
• zwei parallele Geraden

Beispiel: Ebenengleichung aus drei Punkten bestimmen

Gegeben sind die Punkte $A(0,1,2)$, $B(2,0,4)$, $C(4,8,0)$, die nicht auf einer Geraden liegen.

Zum Aufspannen der Ebene wählen wir einen der Punkte als Aufpunkt $\vec{OA}$ und berechnen von dort aus die zwei Spannvektoren $\vec{AB}$, $\vec{AC}$ zu den anderen Punkten.

Aus unseren Punkten ergibt sich beispielhaft folgende Ebenengleichung $E:\vec{x}=\begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix}+s \cdot \begin{pmatrix} 3 \\ {-}1 \\ 2 \end{pmatrix} +t\cdot \begin{pmatrix} 4 \\ 7 \\ {-}2 \end{pmatrix}$.

Die Wahl des Aufpunkts und die daraus resultierende Bestimmung der Spannvektoren ist beliebig. Die Parameterform ist daher nicht eindeutig.

Aufgabe 1: Aufstellen der Parameterform aus der Punkten

Stelle aus den gegebenen Punkten eine Ebenengleichung in Parameterform auf:

a)     $A(1,{-}3,2)$ $B(2,2,15)$ und $C({-}4, 1,{-}5)$

$E:\vec{x}=\begin{pmatrix} 1 \\ {-}3 \\ 2 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 5 \\ 13 \end{pmatrix}+s\cdot \begin{pmatrix} {-}5 \\ 4 \\ {-}7 \end{pmatrix}$ .

b)     $A(1, 10, 7)$ $B(12,4,3)$ und $C(2,1,2)$

$E:\vec{x}=\begin{pmatrix} 1 \\ 10 \\ 7 \end{pmatrix}+r \cdot \begin{pmatrix} 11 \\ {-}6 \\ {-}4 \end{pmatrix}+s\cdot \begin{pmatrix} 1 \\ {-}9 \\ {-}5 \end{pmatrix}$ .

Kannst du hierzu auch jeweils zweite Ebenengleichung aufstellen, die die gleiche Ebene beschreibt?

weitere mögliche Parameterform zu a) $E:\vec{x}=\begin{pmatrix} 2 \\ 2 \\ 15 \end{pmatrix}+r \cdot \begin{pmatrix} {-}1 \\ {-}5 \\ {-}13 \end{pmatrix}+s\cdot \begin{pmatrix} {-}6 \\ {-}1 \\ {-}20 \end{pmatrix}$

weitere mögliche Parameterform zu b) $E:\vec{x}=\begin{pmatrix} 12 \\ 4 \\ 3 \end{pmatrix}+r \cdot \begin{pmatrix} {-}11 \\ 6 \\ 4 \end{pmatrix}+s\cdot \begin{pmatrix} {-}10 \\ {-}3 \\ {-}1 \end{pmatrix}$

Aufgabe 2: Fehlersuche

Furkan und Diego haben versucht zu drei gegebenen Punkten $A(5,4,1), B(2,{-}6,3), C(3,0,8)$ eine Parameterdarstellung einer Ebene aufzustellen. Beurteile inwiefern ihnen das gelungen ist.

Furkans Rechnung

Diegos Rechnung

Mögliche Begründungen: Furkans Rechnung ist nicht richtig. Er hat statt der Spannvektoren $\vec{AB}$ und $\vec{AC}$ die Ortsvektoren zu den Punkten $B$ und $C$ angegeben.

Diegos Rechnung ist richtig. Er hat als Stützvektor den Ortsvektor zum Punkt $C$ gewählt und als Spannvektoren die Vektoren $\vec{CA}$ und $\vec{CB}$. Er hätte noch, wie Furkan es gemacht hat, dazuschreiben können, dass es nur eine der möglichen Parameterformen ist.

Aufgabe 3: Lückentext zur Parameterform

Bearbeite das folgende Applet. Du kannst damit dein Wissen zur Parameterform einer Ebene überprüfen.

Die Punktprobe

Merksatz: Die Punktprobe

Setzt man in die Ebenengleichung in Parameterform für die Variablen $s$ und $t$ Zahlen ein, erhält man den Ortsvektor zu einem Punkt in der Ebene.

Möchte man wissen, ob ein Punkt $P$ in der Ebene liegt, kann man umgekehrt den Ortsvektor $\vec{OP}$ für den Vektor $\vec{x}$ einsetzen und ein lineares Gleichungssystem aufstellen.

Ist das Gleichungssystem eindeutig lösbar, so liegt der Punkt in der Ebene.

Beispiel: Punktprobe

Liegt der Punkt $A({-}1,1,{-}1)$ in der Ebene $E:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} {-}2 \\ 0 \\ 3 \end{pmatrix} +t\cdot \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}$? Wenn ja, dann müsste der zu $A$ gehörende Ortsvektor $\vec{OA} = \begin{pmatrix} {-}1 \\ 1 \\ {-}1 \end{pmatrix}$ die Ebenengleichung erfüllen, d.h. es müsste ein Paar reeller Zahlen $r,s$ geben, für die gilt:

$\vec{OA}=\vec{p}+r \cdot \vec{u}+s \cdot \vec{v}$

$\begin{pmatrix} {-}1 \\ 1 \\ {-}1 \end{pmatrix}=\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} {-}2 \\ 0 \\ 3 \end{pmatrix} +t\cdot \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}$

Die Vektorgleichung ist gleichbedeutend mit dem System der Koordinatengleichungen

$\begin{array}{crcrcr}\\ \text{I}\quad & {-}2r & + & 0s & = & {-}2\\ \text{II}\quad & 0r & + & 1s & = & {-}1\\ \text{III}\quad & 3r & + & 4s & = & {-}1 \end{array}$

Aus der ersten Gleichung folgt $r=1$, die zweite Gleichung ergibt $s={-}1$.

Die dritte Gleichung ist für diese Werte ebenfalls erfüllt, das heißt der Punkt $A$ liegt in der Ebene $E$.

Aufgabe 4: Die Parameterform im Sachzusammenhang

Das Dach einer Kirche hat die Form einer geraden quadratischen Pyramide mit einer Höhe von $12$m. $A(0,0,0)$ sind die Koordinaten einer Ecke der Grundfläche des Daches. Die gegenüberliegende Ecke $C$ der Grundfläche hat die Koordinaten $C(6,6,0)$.

a) Bestimme die Koordinaten der fehlenden Eckpunkte $B$ und $D$, sowie der Dachspitze $S$. Stelle die Ebenengleichung der Ebene $E$ auf, in der die Punkte $B$, $C$ und $S$ liegen.

Die Punkte haben die folgenden Koordinaten: Punkt $B (6,0,0)$ Punkt $D (0,6,0)$ Punkt $S (3,3,12)$. Die Koordinaten des Punktes $S$ kannst du bestimmen, in dem du annimmst, dass die Spitze mittig auf der Grundfläche steht. Die $x_1$-Koordinate kann somit durch $\frac{1}{2} \cdot \vec{AB}$ berechnet werden und die $x_2$-Koordinate durch $\frac{1}{2} \cdot \vec{BC}$. Alternativ könntest du auch die $x_1$- und die $x_2$-Koordinate mithilfe der Diagonalen, also $\frac{1}{2} \cdot \vec{AC}$ berechnen.

Eine mögliche Parameterform der Ebene E wäre: $E: \vec{x}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} +t\cdot \begin{pmatrix} {-}3 \\ 3 \\ 12 \end{pmatrix}$

Falls du noch weiter üben willst, kannst du auch die Ebenengleichungen der übrigen Dachseiten und der Grundfläche bestimmen.

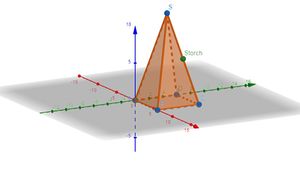
b) Der Naturschutzbund NABU hat bei verschiedenen Störchen Peilsender am Fuß angebracht, die dauerhaft den Standort der Tiere übermitteln. Sie haben für einen der Störche die Koordinaten $(4{,}5, 4{,}5, 6)$ übermittelt. Befindet sich der Storch in der Ebene der in a) errechneten Ebene? Beurteile, ob der Storch auf dem Dach sitzt.

Um herauszufinden, ob die übermittelten Koordinaten in der Ebene liegen, kannst du eine Punktprobe durchführen.

$\begin{pmatrix} 4{,}5 \\ 4{,}5 \\ 6 \end{pmatrix}=\begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix}+s \cdot \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} +t\cdot \begin{pmatrix} {-}3 \\ 3 \\ 12 \end{pmatrix}$

Für das zugehörige Gleichungssystem ergibt sich:

$\begin{array}{crcrcrcr}\\ \text{I}\quad & 6 & + & 0s & + & {-}3t & = & 4{,}5\\ \text{II}\quad & 0 & + & 6s & + & 3t & = & 4{,}5\\ \text{III}\quad & 0 & + & 0s & + & 12t & = & 6 \end{array}$

Aus der ersten und dritten Gleichung folgt $t=0{,}5$. Aus der zweiten Gleichung folgt dann durch Einsetzen von $t=0{,}5$: $s=0{,}5$. Das Gleichungssystem ist daher eindeutig lösbar und der Storch befindet sich in der Ebene.

Da es sich bei dem Dach um einen begrenzten Teil der Ebene handelt, muss zunächst betrachtet werden, für welche Werte von $s,t$ der Storch sich auf dem Dach befände. Da die Spannvektoren bereits jeweils die Strecke zu den äußersten Punkten der Ebene beschreiben und diese durch eine Gerade, in dem Fall der Dachkante, verbunden sind, muss gelten: $s+t\le1$. In dem Fall also: $0{,}5+0{,}5=1$. Der Punkt liegt also genau auf der Kante und somit sitzt der Storch auf dem Dach.

Alternativ könnte man es sich geometrisch veranschaulichen, beispielsweise mithilfe von Geogebra:

Aufgabe 5: Wiederholung zur Parameterform

Wenn du deine bisher gesammelten Kenntnisse noch einmal wiederholen möchtest, kannst du das hiermit machen:

Spurpunkte

Erinnerung: Spurpunkte

Unter einem Spurpunkt versteht man den Schnittpunkt einer Geraden mit der Koordinatenebene.

Gegeben ist eine Geradengleichung in Parameterform $g:\vec{x} = \vec{p} + s \cdot \vec{u}$.

Gesucht sind die Spurpunkte der Geraden. Da es im dreidimensionalen Raum drei Koordinatenebenen gibt

(die $x_1-x_2$, $x_1-x_3$ und $x_2-x_3$-Ebene)

lassen sich drei Spurpunkte berechnen.

$S_1$ ist der Schnittpunkt von Gerade und $x_2-x_3$-Ebene

$S_2$ ist der Schnittpunkt von Gerade und $x_1-x_3$-Ebene

$S_3$ ist der Schnittpunkt von Gerade und $x_1-x_2$-Ebene

Berechnung der Spurpunkte

Den Spurpunkt $S_1$ berechnet man folgendermaßen:

1. Setze die erste Koordinate der Geradegleichung gleich Null und berechne den den dazugehörigen Parameter λ.

2. Setze λ in die Geradegleichung ein, um die Koordinaten des Spurpunktes zu erhalten.

Für $S_2$ und $S_3$ geht man auf gleicher Weise vor.

Beispiel: Spurpunkte berechnen

Gegeben ist die Geradengleichung $g\colon\vec{x}=\begin{pmatrix} 1 \\ {-}4 \\ 4 \end{pmatrix}+s \cdot \begin{pmatrix} 1 \\ 2 \\ {-}1 \end{pmatrix}$

Zum Berechnen von Spurpunkt $S_1$ setzen wir die $x_1$-Koordinate von $S_1$ gleich Null: $S_1(0|?|?)$.

1. $x_1$ = 0 in die erste Zeile der Geradengleichung einsetzen, um $s$ zu berechnen

   $1 + s = 0$ → $s = {-}1$

2. $s$ in die Geradengleichung einsetzt, um den Spurpunkt zu berechnen

$g \colon \vec{s_1}=\begin{pmatrix} 1 \\ {-}4 \\ 4 \end{pmatrix} + {-}1 \cdot \begin{pmatrix} 1 \\ 2 \\ {-}1 \end{pmatrix} = \begin{pmatrix} 0 \\ {-}6 \\ 5 \end{pmatrix}$

Antwort: Der Spurpunkt $S_1$ hat die Koordinaten $(0|{-}6|5)$.

Aufgabe 7: Spurpunkte

Berechne nun die übrigen beiden Spurpunkte $S_2$ und $S_3$ aus dem vorherigen Beispiel und stelle die Ebenengleichung dazu auf.

1.${-}4 + s \cdot 2 = 0$ → $s = 2$

2. $g \colon \vec{s_2}=\begin{pmatrix} 1 \\ {-}4 \\ 4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 1 \\ 2 \\ {-}1 \end{pmatrix} = \begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix}$

$S_2$ hat die Koordinaten $(3|0|2)$.

1. 4 - s = 0 → s = 4

2. $g \colon \vec{s_3}=\begin{pmatrix} 1 \\ {-}4 \\ 4 \end{pmatrix} + 4 \cdot \begin{pmatrix} 1 \\ 2 \\ {-}1 \end{pmatrix} = \begin{pmatrix} 5 \\ 4 \\ 0 \end{pmatrix}$

$S_3$ hat die Koordinaten $(5|4|0)$.

$E \colon \vec{x}=\begin{pmatrix} 0 \\ {-}6 \\ 5 \end{pmatrix}+s \cdot \begin{pmatrix} 3 \\ 6 \\ {-}3 \end{pmatrix} +t \cdot \begin{pmatrix} 5 \\ 10 \\ {-}5 \end{pmatrix}$

{{Box | Aufgabe 8: Spurpunkte berechnen | Gib die Schnittpunkte der Geraden g mit den Koordinatenebenen an (Spurpunkte der Geraden)

a) $g \colon \vec{x}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 2 \\ 1 \end{pmatrix}$

b) $g\colon \vec{x}=\begin{pmatrix} {-}2 \\ 3 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$

a) $S_1 = (0 I 3 I 2), S_2 = (1{,}5 I 0 I 0{,}5), S_3 = (2 I {-}1 I 0)$

b) $S_1 = (0 I 5 I 5), S_2 = ({-}5 I 0 I 5), S_3$ kann in diesem Fall nicht berechnet werden. Was heißt dies für unsere Gerade?

Arbeitsmethode

{{Box | Aufgabe 9: Spurpunkte berechnen (Textaufgabe) | In einem Koordinatensystem mit der Einheit m (Meter) befindet sich ein U-Boot im Punkt $A({-}6713 I 4378 I {-}256)$ und taucht auf einem Kurs in Richtung des Vektors $\vec{u}=\begin{pmatrix} 63 \\ {-}71 \\ 8 \end{pmatrix}$ nach oben auf. In welchem Punkt $P$ erreicht das U-Boot die Meeresoberfläche, wenn es seinen Kurs beibehält?

Arbeitsmethode

⭐ Normalenvektor

Erinnerung: Normalenvektor

Ein Normalenvektor ist ein Vektor, der senkrecht (orthogonal) auf einer Ebene steht, das heißt, dass er orthogonal zu allen Spannvektoren der Ebene ist.

Er wird üblicherweise mit dem Buchstaben $\vec{n}$ bezeichnet.

Alle Normalenvektoren einer Ebene sind Vielfache voneinander.

Berechnung des Normalenvektors

Du benötigst für die Berechnung zwei Gleichungen. Die erste Gleichung erhältst du durch das Vektorprodukt des ersten Spannvektors mit dem Normalenvektor $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix}$, das du gleich Null setzt. Um die zweite Gleichung zu erhalten führst du diesen Schritt nun mit dem zweiten Spannvektor durch. Diese beiden Gleichungen bilden im Folgenden ein Gleichungssystem.

Löse das Gleichungssystem, indem du eine der drei Unbekannten beliebig wählst und die anderen beiden Unbekannten berechnest.

Stehen für eine willkürliche Festlegung mehrere Unbekannte zur Auswahl, so wähle am Besten diejenige mit dem betragsmäßig größten Koeffizienten in der Gleichung und setze sie gleich eins.

Aufgabe 10⭐: Normalenvektor berechnen

Gegeben sei die Ebenengleichung in Parameterform $E \colon \vec{x}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}+r \cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} +s \cdot \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix}$.

Berechne den Normalenvektor der Ebene.

I $\begin{pmatrix} n1 \\ n2 \\ n3 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} = 0$ und II $\begin{pmatrix} n1 \\ n2 \\ n3 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 2 \\ {-}1 \end{pmatrix} = 0$

Wir erhalten ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten. Da mehr Unbekannte vorliegen als Gleichungen ist das LGS nicht eindeutig lösbar!

$\begin{array}{crcrcr}\\ \text{I}\quad  & 1n_1 & + & 2n_2 & + & 1n_3 & = & 0\\ \text{II}\quad & 2n_1 & + & 2n_2 & - & 1n_3 & = & 0 \end{array}$

Es gibt hier zwei Berechnungsmöglichkeiten - per Hand oder per Taschenrechner. Wollte ihr das Gleichungssystem per Hand lösen, würde es sich in diesem Fall anbieten Gleichung I und II zu addieren, damit $n_3$ wegfällt. Wir erhalten mit

$\begin{align}                & & 3n_1 + 4n_2 &= 0        & &\mid -4n2\\ \Leftrightarrow & & 3n_1 &= {-}4n_2            & &\mid :(-4)\\ \Leftrightarrow & &      -tfrac{3}{4} &= n_2 \end{align}$

den allgemeinen Normalenvektor in Abhängigkeit von $n_1$:

$\vec{n} = \begin{pmatrix} n1 \\ tfrac{3}{4} n1 \\ tfrac{1}{2} n1 \end{pmatrix}$

Für einen speziellen Normalenvektor wählen wir für $'''n_1'''$ eine beliebige Zahl aus. Die wählen wir so, dass insgesamt schöne Zahlen raus kommen. Wenn $'''n_1 = 4'''$ ist, dann folgt für $'''n_2 = 3'''$ und für $'''n_3 = 2'''$ .

Daraus folgt für den speziellen Normalenvektor $\vec{n} = \begin{pmatrix} 4 \\ -3 \\ 2 \end{pmatrix}$

⭐ Normalenform und Koordinatenform von Ebenengleichungen

Merksatz: Normalen- und Koordinatenform

Bisher wurde eine Ebene mithilfe eines Aufpunkts A und zwei Spannvektoren $\vec{u}$ und $\vec{v}$ beschrieben. Eine andere Möglichkeit ist, sie durch einen Aufpunkt A und einen Normalenvektor $\vec{n}$ zu beschreiben. Damit erhält man die Normalengleichung der Ebene. Sie hat die Form $E\colon \vec{x}=(\vec{x}-A) \cdot \vec{n}=0$.

Zusätzlich lässt sich jede Ebene E ebenfalls beschreiben durch eine Koordinatengleichung der Form $E\colon ax_1+bx_2+cx_3=d$. Dabei muss mindestens einer der Koeffizienten a, b, c ungleich null sein.

Ist $E\colon ax_1+bx_2+cx_3=d$ eine Koordinatengleichung der Ebene E, so ist $\begin{pmatrix} a \\ b \\ c \end{pmatrix}$ ein Normalenvektor dieser Ebene.

⭐Aufgabe 9: Aufstellen von Normalen- und Koordinatenform

Eine Ebene durch $P(4|1|3)$ hat den Normalenvektor $\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}$

a) Gebe eine Normalengleichung der Ebene an.

$E\colon \vec{x}=[\vec{x}-\begin{pmatrix} 4 \\ 1 \\ 3 \end{pmatrix}] \cdot \begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}=0$ .

b) Bestimme aus der Normalengleichung eine Koordinatengleichung der Ebene

Mit dem Normalenvektor $\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}$ ergibt sich für die Koordinatengleichung der Ansatz: $E\colon 2x_1+x_2+5x_3=d$ mit $d=\vec{OA} \cdot \vec{v}$. Den Wert für $d$ berechnet man indem man die Koordinaten des Punktes $P(4|1|3)$ einsetzt für $x_1, x_2, x_3$ einsetzt.

Lösung:$E\colon 2x_1+x_2+5x_3=22$

c) Liegt der Punkt $A(1|1|1)$ in der Ebene?

Eine Punktprobe mithilfe der Koordinatenform einer Ebenengleichung führt man durch, indem man die Koordinaten für die Parameter $x_1, x_2, x_3$ in die Gleichung einsetzt und kontrolliert, ob die Aussage wahr ist.

$2 \cdot 1 - 1 \cdot 1 + 5 \cdot 1=6 \neq 22$. Der Punkt A liegt nicht in der Ebene.

⭐Aufgabe 10: Aufstellen der Normalenform

Bestimme für die Ebene in der Abbildung eine Gleichung in der Normalenform.

mögliche Lösung: $Q(2|1|3)$ ist der Aufpunkt. Den Normalenvektor berechnen wir mithilfe des Punktes $P({-}1|2|{-}3)$. Damit ist $\vec{n}=\vec{QP}$, d.h. $\vec{n}=\begin{pmatrix} -1-2 \\ 2-1 \\ -3-3 \end{pmatrix}$.

Normalengleichung:$E\colon \vec{x}=[\vec{x}-\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}] \cdot \begin{pmatrix} -3 \\ 1 \\ -6 \end{pmatrix}=0$

⭐Aufgabe 11: Modellierung eines Tisches (Normalenform)

Ein Tischfuß zeigt von einem Punkt $P(4|5|0)$ des Fußbodens aus nach oben, die Tischplatte ist 8 Einheiten vom Boden entfernt. Bestimme eine Normalengleichung der Ebene, in der die Tischplatte liegt.

$T(4|5|8)$ ist der Punkt, in dem das Tischbein auf die Tischplatte trifft, liegt somit in der Ebene der Tischplatte und dient als Aufpunkt der Ebenengleichung. Den Normalenvektor berechnen wir nach dem gleichen Verfahren wie bereits in der vorherigen Aufgabe durch die Berechnung von $\vec{TP}$.

Normalengleichung:$E\colon \vec{x}=[\vec{x}-\begin{pmatrix} 4 \\ 5 \\ 8 \end{pmatrix}] \cdot \begin{pmatrix} 0 \\ 0 \\ -8 \end{pmatrix}=0$

⭐Aufgabe 12: Marktplatzaufgabe (Koordinatenform)

Die folgende Abbildung zeigt eine Karte des Marktplatzes in Bremen mit dem Rathaus, dem Dom und weiteren sehenswürdigen Gebäuden. Legt man ein Koordinatensystem mit dem Koordinatenursprung in der Mitte des Marktplatzes, sodass die $x_1$-Achse nach Süden, die $x_2$-Achse nach Osten und die $x_3$-Achse senkrecht zum Himmel zeigt. Vor dem Rathaus nimmt Höhe des Marktplatzes nach Südwesten leicht ab. Dieser schräge Teil des Marktplatzes soll durch eine Ebene $E\colon \vec{x} = \begin{pmatrix} 42 \\ 20 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} 28 \\ 24 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} -21 \\ 10 \\ 0,5 \end{pmatrix}$ beschrieben werden.

a) Berechne einen möglichen Normalenvektor der Ebene E.

Ein Normalenvektor $\vec{n}$ muss zu den Spannvektoren orthogonal (senkrecht) sein.

Also ist $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} 28 \\ 24 \\ 0 \end{pmatrix}=0$ und $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} -21 \\ 10 \\ 0,5 \end{pmatrix}=0$.

Hieraus folgt das Gleichungssystem:

I $28n_1+24n_2=0$

II $-21n_1+10n_2+0,5n_3=0$.

Wählt man z.B. $n_1=6$ folgt durch Einsetzen in das Gleichungssystem und Umformen: $n_2=-7$ und $n_3=392$. Normalenvektor: $\begin{pmatrix} 6 \\ -7 \\ 392 \end{pmatrix}$

b) Bestimme eine Koordinatengleichung der Ebene E

$E\colon 6x_1-7x_2+392x_3=0$ .

Vor dem Rathaus steht das Denkmals „Roland von Bremen“ mit standhaftem Blick auf dem Dom. Sein Fußpunkt ist $R(-30|20|z)$. Er wurde genau vertikal, d.h. senkrecht auf der $x_1x_2$-Ebene errichtet.

c) Berechne die Zahl z derart, dass R in der Ebene liegt.

$6 \cdot (-30) - 7 \cdot 20 + 392z=0$

$\Leftrightarrow -180-140+392z=0$

$\Leftrightarrow -320+392z=0$

$\Leftrightarrow 392z=320$

$\Leftrightarrow z=0,8163$

.

⭐Aufgabe 13: Schattenwurf (Gerade und Ebene in Koordinatenform)

Ein Baum mit dem Fußpunkt $F({-}2|1|0)$ und der Spitze $S({-}2|1|15)$ wird von der Sonne bestrahlt, deren Sonnenstrahlen parallel zum Vektor $\begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}$ verlaufen. Der Baum wirft einen Schatten auf einen Hang, der durch die Ebene $E\colon x_1+2x_2+x_3={-}6$ beschrieben wird.

Wo liegt der Schattenpunkt T der Baumspitze S auf dem Hang und wie lang ist der Schatten des Baumes?

Der Schattenpunkt T entspricht dem Schnitt der Ebene E mit der Geraden, die durch S verläuft und den Richtungsvektor der Sonnenstrahlen besitzt.

Geradengleichung: $E\colon \vec{x}=\begin{pmatrix} -2 \\ 1 \\ 15 \end{pmatrix}+s \cdot \begin{pmatrix} 4 \\ 5 \\ 7 \end{pmatrix}$

Einsetzen der Zeilen der Geradengleichung in die Ebenengleichung:

$-2+4r+2(1+5r)+(15+7r)=-6.$

Durch Umformen und Ausmultiplizieren erhält man: $r=-1$

Einsetzen von $r=-1$ in die Geradengleichung ergibt den Schnittpunkt $T({-}6|{-}4|8)$.

Schattenlänge des Baumes: $\vert{\vec{FT}}\vert= \vert{\begin{pmatrix} -4 \\ -5 \\ 8 \end{pmatrix}}\vert =\sqrt{16+25+64}=\sqrt{105}$ LE.

⭐Aufgabe 14: Reflexion zur Koordinatenform

a) Warum muss bei einer Koordinatengleichung $E\colon ax_1+bx_2+cx_3=d$ einer Ebene E mindestens einer der Koeffizienten $a, b, c$ ungleich null sein?

Angenommen alle Koeffizienten sind gleich Null: Dann fallen alle Variablen weg und die Gleichung $0=d$ beschreibt keine Ebene mehr.

b) Begründe: Unterscheiden sich die Koordinatengleichungen der Form $E\colon ax_1+bx_2+cx_3=d$ von zwei Ebenen nur in der Konstanten d, dann sind die Ebenen zueinander parallel.

Wenn sich die beiden Ebenengleichungen nur in d unterscheiden haben sie den gleichen Normalenvektor $\vec{n}$, der orthogonal zur Ebene liegt. Damit müssen die Ebenen parallel sein.

c) Beurteile: Alle Ebenen, bei denen in der Koordinatengleichung $E\colon ax_1+bx_2+cx_3=d$ die Koeffizienten $a$ und $b$ ungleich Null, aber $c=0$ ist, haben eine Gemeinsamkeit.

Die Aussage ist wahr, da all diese Ebenen parallel zur $x_3$-Achse liegen.

⭐Überführung der Parameterform in die Koordinatenform

Beispiel: Von der Parameter- zur Koordinatenform einer Ebenengleichung

Wir suchen die Koordinatengleichung der Ebene $E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 5 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}$. Ein Normalenvektor $\vec{n}=\begin{pmatrix} 2 \\ -1 \\ 5 \end{pmatrix}$ muss zu den Spannvektoren $\begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}$ und $\begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}$ orthogonal (senkrecht) sein, also ist $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -1 \\ 0 \end{pmatrix}=0$ und $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 4 \end{pmatrix}=0$. Hieraus folgt $n_1-n_2=0$ $n_1-3n_2+4n_3 =0$. Wählt man z.B. $n_2=2$, so erhält man durch Einsetzen in die Gleichungen des Gleichungssystems und Umformen $n_1=2$ und $n_3=1$ und damit $\vec{n}=\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix}$. Ansatz für die Koordinatengleichung: $E\colon 2x_1+2x_2+x_3=d$. Man berechnet $d$ indem man für $x_1, x_2$ und $x_3$ die Koordinaten des Stützvektors von E einsetzt: $d=2 \cdot 2 + 2 \cdot 1 + 1 \cdot 5=11$. Koordinatengleichung: $E\colon 2x_1+2x_2+x_3=11$

⭐Aufgabe 15: Koordinatengleichung aus Parametergleichung

Bestimme eine Koordinatengleichung der Ebene $E\colon \vec{x} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + s \cdot \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}+ t \cdot \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}$.

Ein Normalenvektor $\vec{n}$ muss zu den Spannvektoren orthogonal (senkrecht) sein.

Also ist $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 3 \\ 0 \end{pmatrix}=0$ und $\begin{pmatrix} n_1 \\ n_2 \\ n_3 \end{pmatrix} \cdot \begin{pmatrix} -2 \\ 1 \\ 3 \end{pmatrix}=0$.

Hieraus folgt das Gleichungssystem

$n_1+3n_2=0$

$-2n_1+n_2+3n_3=0$.

Wählt man z.B. $n_1=9$ folgt durch Einsetzen in das Gleichungssystem und Umformen: $n_2=-3$ und $n_3=7$.

Normalenvektor: $\begin{pmatrix} 9 \\ -3 \\ 7 \end{pmatrix}$.

Das $d$ berechnen wir durch $d=\vec{n} \cdot \vec{OA}$:

$2 \cdot 9 - 3 \cdot 1 + 7 \cdot 2=29$

Koordinatenform der Ebenengleichung: $9x_1 - 3x_2 + 7x_3=29$

⭐Aufgabe 16: Parameter-, Normalen- und Koordinatengleichung

Die Ebene E ist durch die drei Punkte $A(7|2|{-}1)$, $B(4|1|3)$, $C(1|3|2)$ festgelegt. Bestimme eine Parametergleichung, eine Normalengleichung und eine Koordinatengleichung der Ebene E.

$E\colon \vec{x} = \begin{pmatrix} 7 \\ 2 \\ 1 \end{pmatrix} + s \cdot \begin{pmatrix} -3 \\ -1 \\ 4 \end{pmatrix}+ t \cdot \begin{pmatrix} -6 \\ 1 \\ 3 \end{pmatrix}$

$E\colon \vec{x}=(\vec{x}-\begin{pmatrix} 7 \\ 2 \\ -1 \end{pmatrix}) \cdot \begin{pmatrix} -7 \\ -15 \\ -9 \end{pmatrix}=0$

$-7x_1-15x_2-9x_3=70$