Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 227: | Zeile 227: | ||
{{Box | Beispiel: Berechnung des Winkels zwischen Gerade und Ebene | | {{Box | Beispiel: Berechnung des Winkels zwischen Gerade und Ebene | | ||
Gegeben sind die Gerade <math>g | Gegeben sind die Gerade <math>g\colon \vec{x}=\left( \begin{matrix} {-}1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E: 2x_1 + x_2 + 4 x_3 = {-}27 </math>. Bestimme den Winkel, unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | ||
'''1. Schritt''': Notiere den Richtungvektor <math> \vec{u} </math> der Gerade und den Normalenvektor <math> \vec{n} </math> der Ebene. | '''1. Schritt''': Notiere den Richtungvektor <math> \vec{u} </math> der Gerade und den Normalenvektor <math> \vec{n} </math> der Ebene. | ||
| Zeile 251: | Zeile 251: | ||
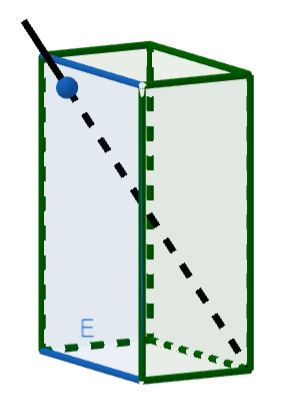
Jedes Trinkpäckchen hat die Form eines Quaders (siehe Abbildung). Die Seite, auf der sich das Loch für den Strohhalm befindet, kann durch die Ebene <math>F: x_1=5 </math> beschrieben werden. | Jedes Trinkpäckchen hat die Form eines Quaders (siehe Abbildung). Die Seite, auf der sich das Loch für den Strohhalm befindet, kann durch die Ebene <math>F: x_1=5 </math> beschrieben werden. | ||
Wenn der Strohhalm so in das Trinkpäckchen gesteckt wird, das er in der hintersten Ecke anstößt, kann er durch die Gerade <math>g </math> veranschaulicht werden: <math> g | Wenn der Strohhalm so in das Trinkpäckchen gesteckt wird, das er in der hintersten Ecke anstößt, kann er durch die Gerade <math>g </math> veranschaulicht werden: <math> g\colon \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} {-}5\\ 6\\ {-}11 \end{pmatrix}</math>. | ||
{{Lösung versteckt|1= Vielleicht hilft dir die Skizze.|2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1= Vielleicht hilft dir die Skizze.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
| Zeile 290: | Zeile 290: | ||
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math>z=3 \sqrt{5} \approx 6,71</math>. | Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math>z=3 \sqrt{5} \approx 6,71</math>. | ||
Somit kann im letzten Schritt die Gerade <math>g</math> aufgestellt werden. Man erhält <math> g | Somit kann im letzten Schritt die Gerade <math>g</math> aufgestellt werden. Man erhält <math> g\colon \vec{x} = \left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 3\\ 6\\ {3 \sqrt{5}} \end{matrix} \right) </math>. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode}} | | Arbeitsmethode}} | ||
| Zeile 333: | Zeile 333: | ||
{{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Parameterform | | ||
Gegeben sind eine Ebene <math>E | Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 1\\ 4\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} 1\\ {-}2\\ 1 \end{matrix} \right) + t \cdot \left( \begin{matrix} 3\\ 1\\ {-}1 \end{matrix} \right) </math> und eine Ebene <math>F\colon \vec{x}=\left( \begin{matrix} 1\\ 2\\ 3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 2\\ 3\\ {-}2 \end{matrix} \right)+ u \cdot \left( \begin{matrix} 5\\ 4\\ {-}3 \end{matrix} \right)</math>. | ||
Untersuche die Lagebeziehung der beiden Ebenen. | Untersuche die Lagebeziehung der beiden Ebenen. | ||
| Zeile 389: | Zeile 389: | ||
{{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform | | {{Box | Beispiel: Untersuchung der Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform | | ||
Gegeben sind eine Ebene <math>E | Gegeben sind eine Ebene <math>E\colon \vec{x}=\left( \begin{matrix} 2\\ 1\\ {-}3 \end{matrix} \right) + r \cdot \left( \begin{matrix} 1\\ 0\\ {-}1 \end{matrix} \right) + s \cdot \left( \begin{matrix} 2\\ 1\\ 0 \end{matrix} \right) </math> und eine Ebene <math>F: -1{,}5x_1+3x_2-1{,}5x_3=4,5</math>. | ||
Untersuche die Lagebeziehung der beiden Ebenen. | Untersuche die Lagebeziehung der beiden Ebenen. | ||
| Zeile 427: | Zeile 427: | ||
'''a)''' <math>E | '''a)''' <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 0 \\ {-}1 \\ 2 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} </math> | ||
<math>F: 7x_1+x_2-3x_3-8=0 </math> | <math>F: 7x_1+x_2-3x_3-8=0 </math> | ||
| Zeile 435: | Zeile 435: | ||
'''b)''' <math>E | '''b)''' <math>E\colon \vec{x} = \begin{pmatrix} -3 \\ 1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix}+ s \cdot \begin{pmatrix} -1 \\ 0 \\ 3 \end{pmatrix} </math> | ||
<math>F: -3x_1-9x_2-x_3=5 </math> | <math>F: -3x_1-9x_2-x_3=5 </math> | ||
| Zeile 441: | Zeile 441: | ||
{{Lösung versteckt|1= parallel|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1= parallel|2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''c)''' <math>E | '''c)''' <math>E\colon \vec{x} = \begin{pmatrix} 2 \\ {-}1 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0{,}5 \end{pmatrix}+ s \cdot \begin{pmatrix} 4 \\ {-}2 \\ 1 \end{pmatrix} </math> | ||
<math>F: 2x_1-2x_2-4x_3=-6 </math> | <math>F: 2x_1-2x_2-4x_3=-6 </math> | ||
| Zeile 484: | Zeile 484: | ||
Stelle die Geradengleichung auf. | Stelle die Geradengleichung auf. | ||
<math>g | <math>g\colon \vec{x} = \begin{pmatrix} 0 \\ {-}1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ {-}2 \\ 1 \end{pmatrix} </math>| Hervorhebung1}} | ||
{{Box|Aufgabe 11: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | {{Box|Aufgabe 11: Untersuchung der Lagebeziehung zwischen zwei Ebenen in Koordinatenform | | ||
Gegeben ist eine Ebene <math>E | Gegeben ist eine Ebene <math>E\colon \vec{x}=-2x_1-3x_2+x_3=2 </math>. Untersuche die Lagebeziehung zwischen dieser und den dir angezeigten Ebenen. Ziehe die Ebenen in das entsprechende Feld. | ||
{{LearningApp|width=100%|height=500px|app=pq97ryxmn21}} | {{LearningApp|width=100%|height=500px|app=pq97ryxmn21}} | ||
| Zeile 504: | Zeile 504: | ||
{{Box|Aufgabe 12: Schnitt von zwei Zeltflächen| | {{Box|Aufgabe 12: Schnitt von zwei Zeltflächen| | ||
Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E | Die beiden Seitenflächen eines Zeltes liegen in den Ebenen <math>E\colon \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix} </math> und <math>F\colon \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} {-}1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ {-}3 \\ 4 \end{pmatrix}</math>. Der Erdboden wird durch die <math>x_1</math>-<math>x_2</math> -Ebene aufgespannt. In welcher Höhe befindet sich die obere Zeltkante, wenn eine Einheit im Koordinatensystem <math>50</math> cm entspricht? | ||
{{Lösung versteckt|1= Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1= Mache dir zunächst eine Skizze von der Situation. Überlege dir, womit die obere Zeltkante beschrieben werden kann.|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
| Zeile 523: | Zeile 523: | ||
Die Schnittgerade der beiden Ebenen lautet demnach: | Die Schnittgerade der beiden Ebenen lautet demnach: | ||
<math> g | <math> g\colon \vec{x} = \left( \begin{matrix} 8\\ 3\\ 4 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 0 \end{matrix} \right) </math> | ||
Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der <math>x_3</math>-Koordinate des Vektors bestimmt werden. | Da die Schnittgerade der oberen Zeltkante entspricht, lässt sich aus dem Stützvektor der Geraden die Höhe ablesen. Die Höhe kann mithilfe der <math>x_3</math>-Koordinate des Vektors bestimmt werden. | ||
| Zeile 549: | Zeile 549: | ||
{{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | | {{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | | ||
Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E | Gegeben sind zwei Ebenen <math>E</math> und <math>F</math> mit <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}</math> und <math>F: 7x_1+x_2-3x_3 </math>. Berechne den Schnittpunkt zwischen den Ebenen. | ||
'''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | '''1. Schritt:''' Bestimmte die Normalenvektoren von <math>E</math> und <math>F</math>. | ||
| Zeile 566: | Zeile 566: | ||
{{Box | Aufgabe 13: Schnittwinkel zwischen Ebenen | | {{Box | Aufgabe 13: Schnittwinkel zwischen Ebenen | | ||
Sei <math>E</math> eine Ebene mit <math>E | Sei <math>E</math> eine Ebene mit <math>E\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix}</math> , | ||
<math>F</math> eine Ebene mit <math>F: 2x_1+6x_2-4x_3=2</math>. | <math>F</math> eine Ebene mit <math>F: 2x_1+6x_2-4x_3=2</math>. | ||
und <math>H</math> eine Ebene mit <math>H: 2x_1+4x_2-7x_3=13 </math> . | und <math>H</math> eine Ebene mit <math>H: 2x_1+4x_2-7x_3=13 </math> . | ||
| Zeile 642: | Zeile 642: | ||
{{Box | Aufgabe 15: Bank am Wanderweg | | {{Box | Aufgabe 15: Bank am Wanderweg | | ||
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene <math> S_1 | An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene <math> S_1\colon \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0{,}5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0{,}4 \\ 0\end{pmatrix}, r,s \in [0, 1] </math> und die Rückenlehne durch die Ebene <math>R_1\colon -x_2 + 0{,}4 x_3 = -0{,}2 </math> beschrieben werden kann. | ||
'''a)''' Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen <math>100^{\circ}</math> und <math>110^{\circ}</math> liegen. Überprüfe, ob dies auf die neue Bank zutrifft. | '''a)''' Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen <math>100^{\circ}</math> und <math>110^{\circ}</math> liegen. Überprüfe, ob dies auf die neue Bank zutrifft. | ||
| Zeile 664: | Zeile 664: | ||
'''b)''' [[Datei:Bankaufgabe.png|mini|Skizze: Bänke am Wanderweg]] | '''b)''' [[Datei:Bankaufgabe.png|mini|Skizze: Bänke am Wanderweg]] | ||
Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene <math> S_2 | Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene <math> S_2\colon \vec{x} = \begin{pmatrix} 0 \\ 0,8 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0,4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}</math> und die Rückenlehne der Ebene <math> R_2\colon -x_2 - 0{,}4 x_3 = -1 </math> Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Version vom 9. Mai 2021, 18:43 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
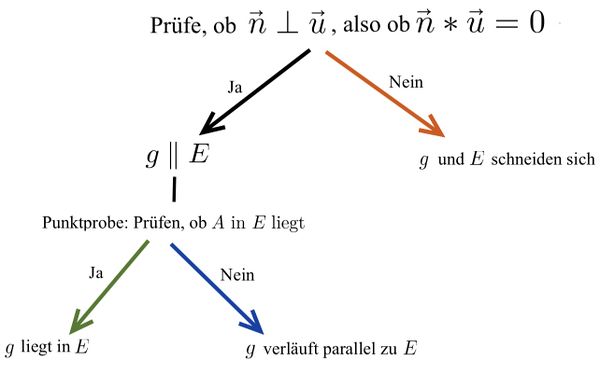
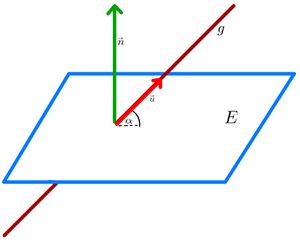
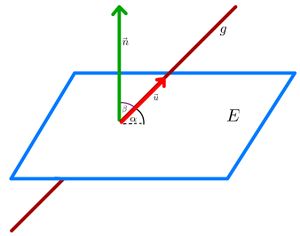
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
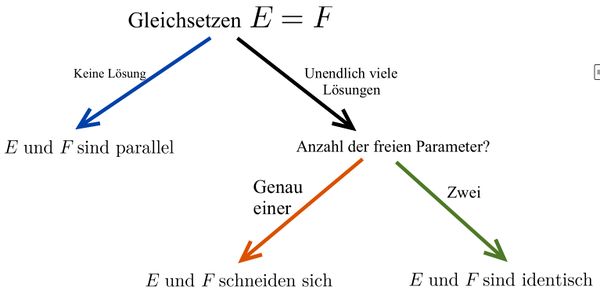
Mögliche Lagebeziehungen zwischen zwei Ebenen
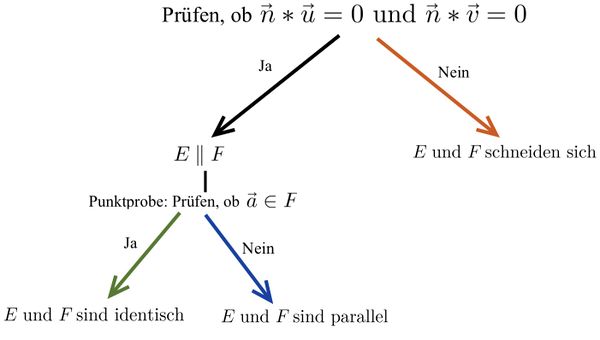
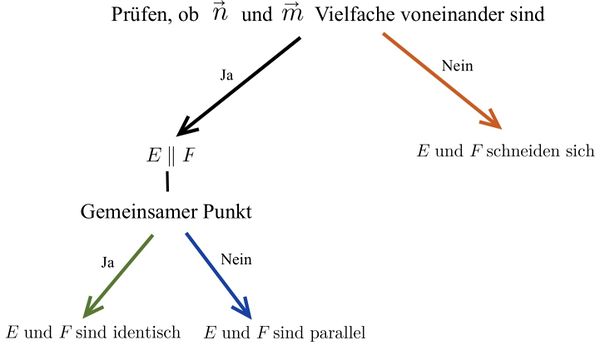
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
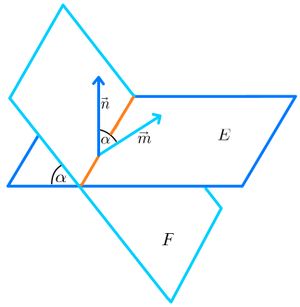
⭐Berechnung des Winkels zwischen Ebene und Ebene