Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 203: | Zeile 203: | ||
{{Box | Merke: Berechnung des Winkels zwischen Gerade und Ebene | Wenn eine Gerade <math>g</math> eine Ebene <math>E</math> schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum]] | Merksatz}} | {{Box | Merke: Berechnung des Winkels zwischen Gerade und Ebene | Wenn eine Gerade <math>g</math> eine Ebene <math>E</math> schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum]] | Merksatz}} | ||
{{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | {{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | ||
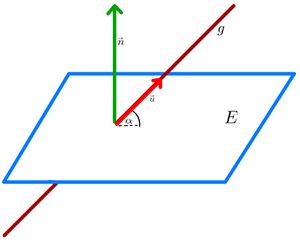
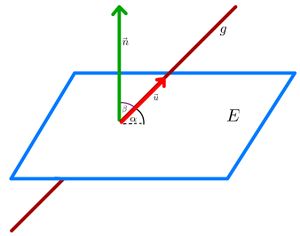
Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>\vec{n}</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>\vec{u}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math> sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math>. Ist | |||
Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>\vec{n}</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>\vec{u}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math> sin(\alpha)=\frac{|\vec{n} \ast \vec{u}|}{|\vec{n}| \cdot |\vec{u}|}</math>. | |||
Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von Gerade und Ebene eingeschlossen werden. Dein berechneter Winkel <math>\alpha</math> darf also nur zwischen <math>0 ^{\circ}</math> und <math>90 ^{\circ}</math> liegen. Ist dein berechneter Winkel <math> \alpha > 90 ^{\circ}</math>, so musst du <math> 180 ^{\circ} - \alpha </math> berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen. | |||
Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen: | Wenn du wissen möchtest, warum du nicht - wie beim Winkel zwischen zwei Geraden - den Kosinus benutzt, kannst du das hier nachlesen: | ||
| Zeile 532: | Zeile 535: | ||
Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum]]. | Merksatz}} | Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel [[Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum]]. | Merksatz}} | ||
{{Box | Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen | Seien <math>E</math> und <math>F</math> zwei sich schneidende Ebenen mit den Normalenvektoren <math>\vec{n}</math> und <math>\vec{m}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>F</math> kann mit folgender Formel berechnet werden: <math> cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}</math>. | {{Box | Merksatz: Formel zur Berechnung des Winkels zwischen zwei Ebenen | | ||
Seien <math>E</math> und <math>F</math> zwei sich schneidende Ebenen mit den Normalenvektoren <math>\vec{n}</math> und <math>\vec{m}</math>. Der Schnittwinkel <math>\alpha</math> zwischen <math>E</math> und <math>F</math> kann mit folgender Formel berechnet werden: <math> cos(\alpha)=\frac{ \vec{n} \ast \vec{m}}{|\vec{n}| \cdot |\vec{m}|}</math>. | |||
Ist | Ist nach dem '''Schnittwinkel''' gefragt, so ist immer der kleinere der beiden Winkel gesucht, die von den Ebenen eingeschlossen werden. Dein berechneter Winkel <math>\alpha</math> darf also nur zwischen <math>0 ^{\circ}</math> und <math>90 ^{\circ}</math> liegen. Ist dein berechneter Winkel <math> \alpha > 90 ^{\circ}</math>, so musst du <math> 180 ^{\circ} - \alpha </math> berechnen, und erhälst so den kleineren der beiden Winkel. In einigen Textaufgaben ist jedoch der größere der beiden Winkel gesucht. Hier können dir Skizzen helfen.| Merksatz}} | ||
{{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | | {{Box | Beispiel: Winkel berechnen zwischen zwei Ebenen | | ||
Version vom 9. Mai 2021, 13:58 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
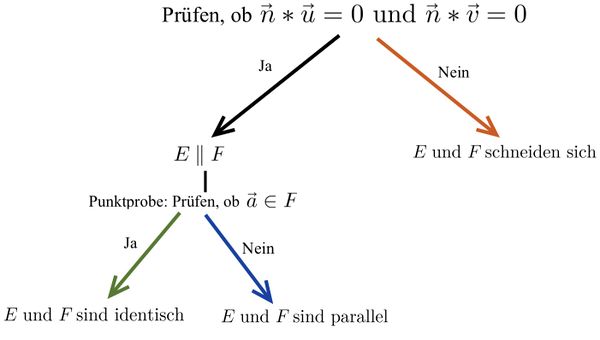
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
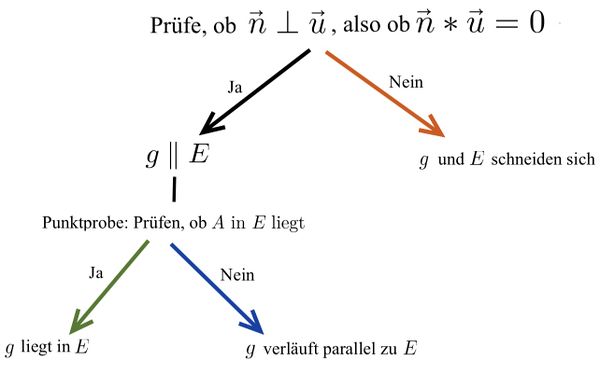
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
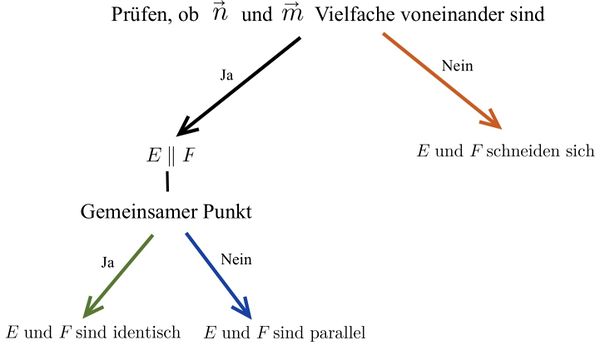
Lagebeziehung Ebene-Ebene
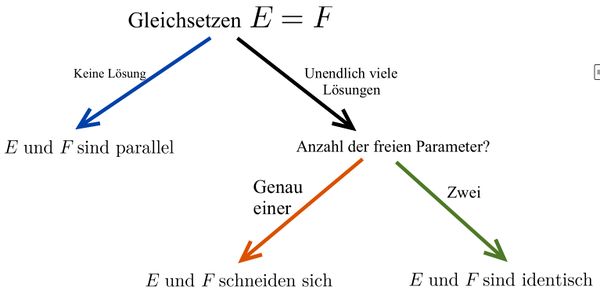
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Beide Ebenengleichungen in Parameterform
⭐Ebenengleichungen in Parameter- und Koordinatenform
⭐Beide Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene