Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 202: | Zeile 202: | ||
[[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg|mini|Abbildung: Winkel zwischen Gerade und Ebene]] | [[Datei:Abbildung Winkel zwischen Gerade und Ebene .jpg|mini|Abbildung: Winkel zwischen Gerade und Ebene]] | ||
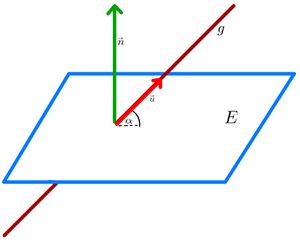
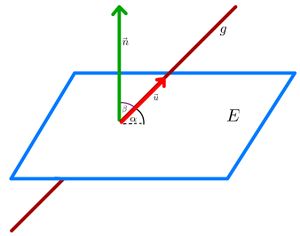
{{Box | | {{Box | Merke: Berechnung des Winkels zwischen Gerade und Ebene | Wenn eine Gerade <math>g</math> eine Ebene <math>E</math> schneidet, kannst du nicht nur den Schnittpunkt berechnen, sondern auch den Schnittwinkel. Dafür benötigen wir den Normalenvektor. Wenn du nicht mehr genau weißt, wie man diesen abliest oder berechnet, schau noch einmal in Kapitel... | Merksatz}} | ||
{{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | {{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | | ||
| Zeile 219: | Zeile 219: | ||
{{Box | Beispiel: | {{Box | Beispiel: Berechnung des Winkels zwischen Gerade und Ebene | | ||
Gegeben sind die Gerade <math>g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) | Gegeben sind die Gerade <math>g: \vec{x}=\left( \begin{matrix} -1\\ 3\\ 6 \end{matrix} \right) + r \cdot \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und die Ebene <math>E: 2x_1 + x_2 + 4 x_3 = -27 </math>. Bestimme den Winkel, unter dem sich die Gerade <math>g</math> und die Ebene <math>E</math> schneiden. | ||
'''1. Schritt''': Notiere den Richtungvektor <math> \vec{u} </math> der Gerade und den Normalenvektor <math> \vec{n} </math> der Ebene. | '''1. Schritt''': Notiere den Richtungvektor <math> \vec{u} </math> der Gerade und den Normalenvektor <math> \vec{n} </math> der Ebene. | ||
<math> \vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und <math> \vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right) </math> | <math> \vec{u}= \left( \begin{matrix} 8\\ 2\\ 0 \end{matrix} \right) </math> und <math> \vec{n}= \left( \begin{matrix} 2\\ 1\\ 4 \end{matrix} \right) </math> | ||
'''2. Schritt''': Setze die Vektoren in die Formel <math> sin(\alpha)=\frac{ \vec{n} \ast \vec{u}}{|\vec{n}| \cdot |\vec{u}|}</math> ein. | '''2. Schritt''': Setze die Vektoren in die Formel <math> sin(\alpha)=\frac{ \vec{n} \ast \vec{u}}{|\vec{n}| \cdot |\vec{u}|}</math> ein. | ||
<math> sin(\alpha)=\frac{ \left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \ast \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|} \Leftrightarrow sin(\alpha)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow sin(\alpha)=\frac{18}{\sqrt{1260}} </math> | <math> sin(\alpha)=\frac{ \left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \ast \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} 2\\ 1\\ 4 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 8\\ 2\\ 0 \end{pmatrix} \right|} \Leftrightarrow sin(\alpha)=\frac{18}{\sqrt{60} \cdot \sqrt{21}} \Leftrightarrow sin(\alpha)=\frac{18}{\sqrt{1260}} </math> | ||
'''3. Schritt''': | '''3. Schritt''': Forme die Gleichung um. | ||
<math> \alpha = sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \alpha \approx 28,45 ^\circ </math> | <math> \alpha = sin^{-1}(\frac{18}{\sqrt{1260}}) \Leftrightarrow \alpha \approx 28,45 ^\circ </math> | ||
Der Winkel beträgt also <math> 28,45 ^\circ </math>. | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
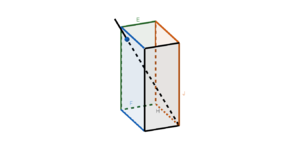
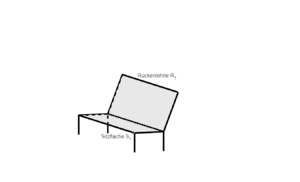
{{Box | Aufgabe | {{Box | Aufgabe 6: Trinkpäckchen | | ||
[[Datei:Trinkpäckchen.png|mini|Abbildung: Trinkpäckchen mit Strohhalm]] | [[Datei:Trinkpäckchen.png|mini|Abbildung: Trinkpäckchen mit Strohhalm]] | ||
| Zeile 252: | Zeile 254: | ||
Der Boden kann durch die Ebene <math>B: x_3=0 </math> und der Deckel durch die Ebene <math> D: x_3=12 </math> beschrieben werden. | Der Boden kann durch die Ebene <math>B: x_3=0 </math> und der Deckel durch die Ebene <math> D: x_3=12 </math> beschrieben werden. | ||
Der Strohhalm kann dabei durch die Gerade <math> g: \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix | Der Strohhalm kann dabei durch die Gerade <math> g: \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix}</math> beschrieben werden. | ||
Eine Schulklasse nimmt auf ihrem Wandertag viele dieser Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Berechne den Winkel, in dem die Kinder den Strohhalm halten müssen, um auch an den Saft in der letzten Ecke zu kommen. | Eine Schulklasse nimmt auf ihrem Wandertag viele dieser Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Berechne den Winkel, in dem die Kinder den Strohhalm halten müssen, um auch an den Saft in der letzten Ecke zu kommen. | ||
| Zeile 275: | Zeile 277: | ||
{{Box | Aufgabe | {{Box | Aufgabe 7: Gerade gesucht | | ||
Eine Gerade <math>g</math> soll die <math>x_1-x_2 | Eine Gerade <math>g</math> soll die <math>x_1-x_2</math>-Ebene in einem Winkel von <math>45 ^\circ</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\begin{pmatrix} 3\\ 6\\ z \end{pmatrix}</math> verläuft. Stelle die Gerade <math>g</math> auf. | ||
{{Lösung versteckt|1=Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | {{Lösung versteckt|1=Notiere dir alle Informationen aus dem Text. Was weißt du über die Berechnung des Winkels zwischen einer Gerade und einer Ebene?|2=Tipp 1 anzeigen|3=Tipp 1 verbergen}} | ||
| Zeile 285: | Zeile 287: | ||
{{Lösung versteckt|1=Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | {{Lösung versteckt|1=Um Gleichungen mit einer Unbekannten zu lösen, kannst du die nSolve-Funktion deines Taschenrechners nutzen.|2=Tipp 3 anzeigen|3=Tipp 3 verbergen}} | ||
{{Lösung versteckt|1=Bisher wurde mit der Formel | {{Lösung versteckt|1=Bisher wurde mit der Formel zur Winkelberechnung nur der Winkel berechnet. Die Formel kann jedoch auch genutzt werden, um bei einem vorgegebenen Winkel die Lage der Gerade oder Ebene zu bestimmen. | ||
Bestimme dafür zuerst den Normalenvektor der Ebene. Da es sich um die <math>x_1-x_2</math> -Ebene handelt, lautet der Normalenvektor <math>\vec{n}=\begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}</math>. | |||
Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel | Nun können der Normalenvektor der Ebene, der Richtungsvektor der Gerade und der vorgegebene Winkel in die Formel eingesetzt werden: <math> sin(45)=\frac{ \left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \ast \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|}{\left| \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 3\\ 6\\ z \end{pmatrix} \right|} \Leftrightarrow sin(45)=\frac{z}{\sqrt{1} \cdot \sqrt{9+36 + z^{2}}} \Leftrightarrow sin(45)=\frac{z}{\sqrt{45+z^{2}}} </math> | ||
Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math>z=3 \sqrt{5} \approx 6,71</math>. | Löst man die Gleichung mithilfe des Taschenrechners, erhält man das Ergebnis: <math>z=3 \sqrt{5} \approx 6,71</math>. | ||
Version vom 9. Mai 2021, 09:41 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
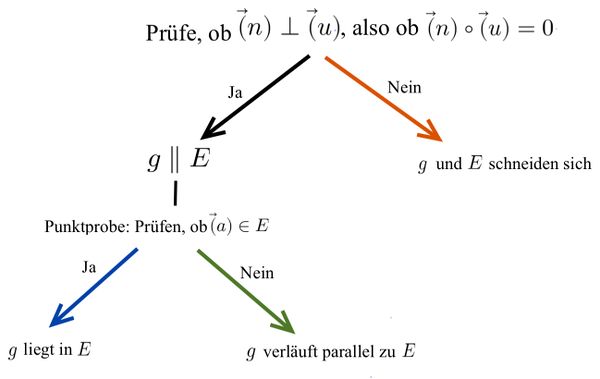
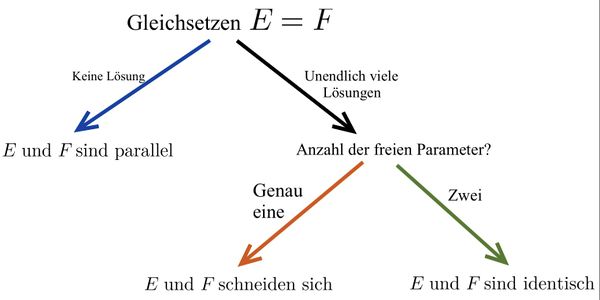
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
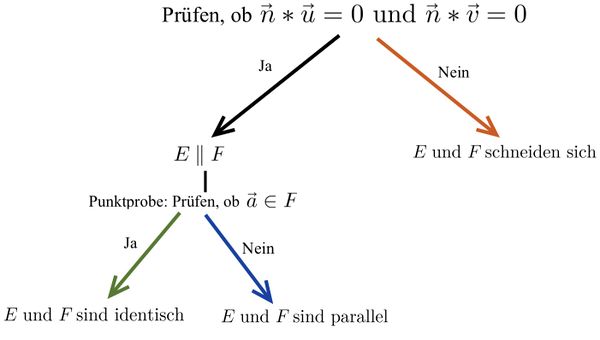
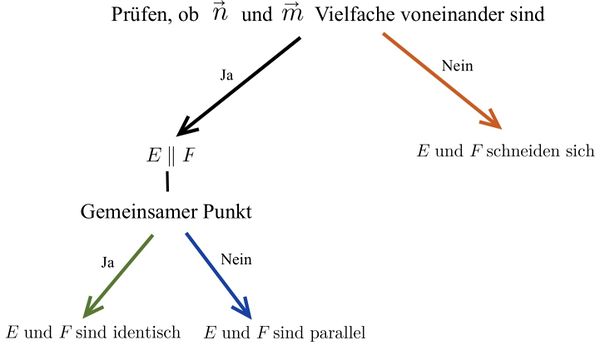
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Zwei Ebenengleichungen in Parameterform
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene