Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 3: | Zeile 3: | ||
[[Datei:Bauarbeiter.jpg|rahmenlos]] | [[Datei:Bauarbeiter.jpg|rahmenlos]] | ||
{{Box | {{Box | ||
|1=Info | |1=Info | ||
|2=In diesem Lernpfadkapitel | |2=In diesem Lernpfadkapitel geht es um die Lagebeziehung zwischen einer Gerade und einer Ebene oder zwischen zwei Ebenen inklusive der Berechnung der Schnittwinkel. | ||
Bei den Aufgaben unterscheiden wir folgende Typen: | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
| Zeile 17: | Zeile 16: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt. | |||
==Lagebeziehung Gerade-Ebene== | ==Lagebeziehung Gerade-Ebene== | ||
===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ===Mögliche Lagebeziehungen zwischen Gerade und Ebene=== | ||
{{Box|Merke:| | {{Box|Merke:| | ||
Zwischen einer | Zwischen einer Geraden und einer Ebene gibt es drei mögliche Lagebeziehungen. | ||
{{3Spalten | {{3Spalten | ||
| | | | ||
| Zeile 32: | Zeile 33: | ||
{{3Spalten | {{3Spalten | ||
| | | | ||
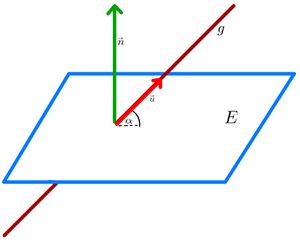
Die | Die Gerade schneidet die Ebene. | ||
| | | | ||
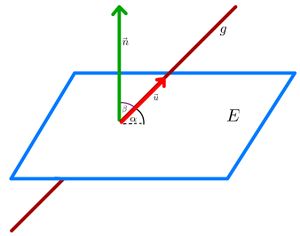
Die Gerade und die Ebene liegen parallel. | Die Gerade und die Ebene liegen parallel. | ||
| Zeile 42: | Zeile 43: | ||
===Untersuchung der Lagebeziehung zwischen Gerade und Ebene=== | ===Untersuchung der Lagebeziehung zwischen Gerade und Ebene=== | ||
{{Box|Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | {{Box|Aufgabe 1: Lückentext zur Lagebeziehung zwischen Gerade und Ebene| | ||
{{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | {{LearningApp|width=100%|height=500px|app=pfhf979bk21}} | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |||
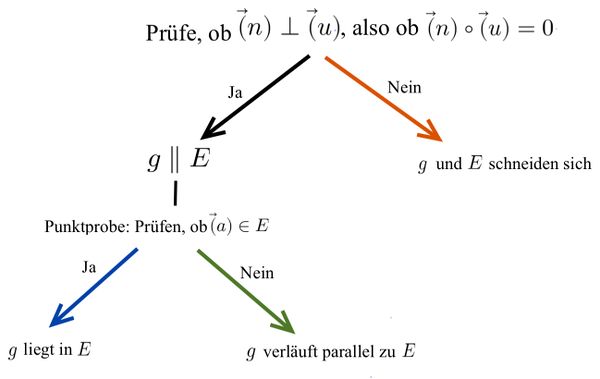
{{Box|Vorgehen: | {{Box|Vorgehen: Untersuchung der Lagebeziehung zwischen Gerade und Ebene | | ||
[[Datei:Vorgehen Lagebeziehung Gerade und Ebene.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen Lagebeziehung Gerade und Ebene.jpg|zentriert|rahmenlos|600x600px]] | ||
|Merksatz}} | |Merksatz}} | ||
{{Box | Beispielaufgabe: Untersuchung der Lagebeziehung | {{Box | Beispielaufgabe: Untersuchung der Lagebeziehung zwischen Gerade und Ebene | | ||
Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math> und eine Gerade <math>g: \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) </math>. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt. | Gegeben sind eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math> und eine Gerade <math>g: \vec{x}=\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) </math>. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt. | ||
| Zeile 73: | Zeile 73: | ||
'''5. Schritt:''' Da sich die Ebene <math>E</math> und die Gerade <math>g</math> schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter <math>r</math> in die Geradengleichung ein: <math>\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ {-}2\\ 2 \end{matrix} \right) </math> | '''5. Schritt:''' Da sich die Ebene <math>E</math> und die Gerade <math>g</math> schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter <math>r</math> in die Geradengleichung ein: <math>\left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ {-}4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ {-}2\\ 2 \end{matrix} \right) </math> | ||
Alternativ kannst du die Parameter <math>s</math> und <math>t</math> in die Ebenengleichung einsetzen und erhältst den gleichen Punkt. | |||
| Hervorhebung1}} | | Hervorhebung1}} | ||
{{Box|Aufgabe: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | {{Box|Aufgabe 2: Untersuchung der Lagebeziehung zwischen Gerade und Ebene| | ||
Gegeben ist eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math>. | Gegeben ist eine Ebene <math>E: \vec{x}=\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) </math>. | ||
| Zeile 91: | Zeile 93: | ||
|Arbeitsmethode | Farbe={{Farbe|orange}}}} | |Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
{{Box | Aufgabe | {{Box | Aufgabe 3: Schatten eines Sonnensegels | | ||
Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math> A = \left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right), B= \left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right)</math> und <math> C = \left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) </math>. Die Terrasse wird modelliert durch die <math>x_1- x_2</math>-Ebene. Die Sonne scheint aus Richtung <math> S = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) </math>. In welchem Bereich hat Frau Meier nun Schatten? | Da es Frau Meier im Sommer auf ihrer Terrasse gerne schattig haben möchte, spannt sie ein dreieckiges Segeltuch auf. Die Eckpunkte des Segeltuchs sind <math> A = \left( \begin{matrix} 9\\ {-}5\\ 7 \end{matrix} \right), B= \left( \begin{matrix} 6\\ {-}5\\ 7 \end{matrix} \right)</math> und <math> C = \left( \begin{matrix} 7\\ {-}10\\ 11 \end{matrix} \right) </math>. Die Terrasse wird modelliert durch die <math>x_1- x_2</math>-Ebene. Die Sonne scheint aus Richtung <math> S = \left( \begin{matrix} -2\\ {-}2\\ {-}10 \end{matrix} \right) </math>. In welchem Bereich hat Frau Meier nun Schatten? | ||
Version vom 9. Mai 2021, 08:57 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Das Lernpfadkapitel ist so aufgebaut, dass ihr in jedem Abschnitt zuerst grundlegende Inhalte mithilfe der Merkkästen wiederholen könnt. Anschließend findet ihr eine Beispielaufgabe, in der die Inhalte veranschaulicht werden. Am Ende jedes Abschnittes gibt es Übungsaufgaben mit Tipps und Lösungen, sodass ihr üben und euch selbst überprüfen könnt.
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
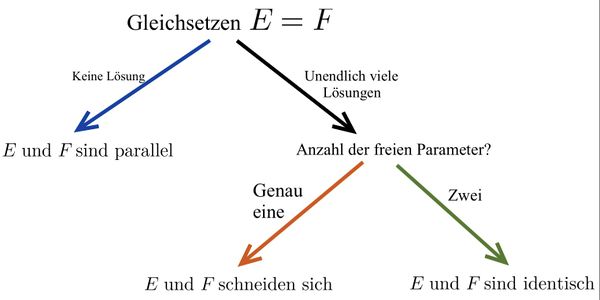
Zwei Ebenengleichungen in Parameterform
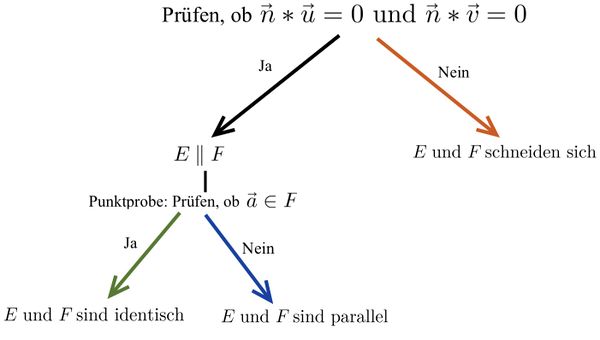
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
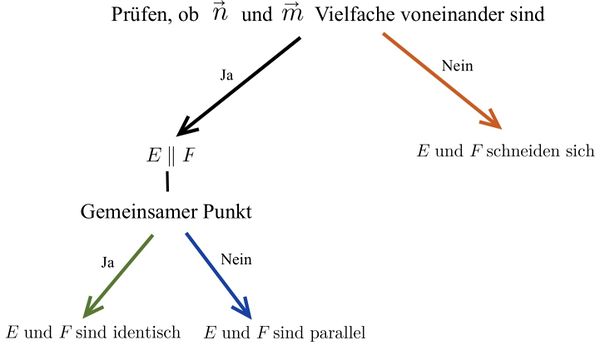
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene