Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 241: | Zeile 241: | ||
<math>E: x_2=0 </math> | <math>E: x_2=0 </math> | ||
<math>F: x_1=5 </math> | <math>F: x_1=5 </math> | ||
<math>H: x_2=8 </math> | <math>H: x_2=8 </math> | ||
<math>J: x_1=0 </math> | <math>J: x_1=0 </math> | ||
| Zeile 249: | Zeile 252: | ||
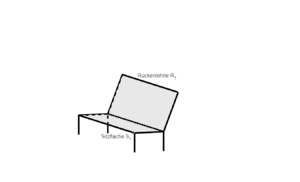
Eine Schulklasse nimmt auf ihrem Wandertag viele dieser Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Kannst du ihnen helfen, in welchem Winkel sie den Strohhalm halten müssen? | Eine Schulklasse nimmt auf ihrem Wandertag viele dieser Trinkpäckchen mit. Einige Kinder ärgern sich, dass sie mit dem Strohhalm nicht gut in die letzte Ecke kommen. Kannst du ihnen helfen, in welchem Winkel sie den Strohhalm halten müssen? | ||
Der Strohhalm kann dabei durch die Gerade <math> g: \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix} t \in \mathbb{R} </math> beschrieben werden. | Der Strohhalm kann dabei durch die Gerade <math> g: \vec{x} = \begin{pmatrix} 5\\ 2\\ 11 \end{pmatrix} + t \cdot \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix}, t \in \mathbb{R} </math> beschrieben werden. | ||
{{Lösung versteckt|1= Überlege zunächst, zwischen welcher Ebene und der Gerade der Winkel berechnet werden muss.|2=Tipp anzeigen|3=Tipp verbergen}} | |||
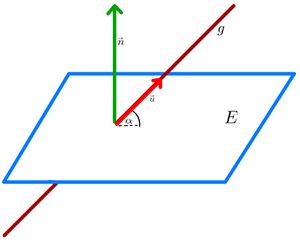
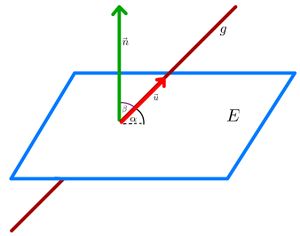
{{Lösung versteckt|1= Gesucht wird der Winkel zwischen der Gerade <math>g</math> und der Ebene <math>F</math>. Der Richtungsvektor der Gerade ist <math> \vec{u} = \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix} </math>. Der Normalenvektor der Ebene kann abgelesen werden: <math> \vec{n} = \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} </math>. | |||
Einsetzen der Vektoren in die Formel liefert: | |||
<math> sin(\alpha)=\frac{ \left| \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix} \ast \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|}{\left| \begin{pmatrix} -5\\ 6\\ -11 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix} \right|} \Leftrightarrow sin(\alpha)=\frac{5}{\sqrt{1} \cdot \sqrt{25+36+121}} \Leftrightarrow sin(\alpha)=\frac{1}{\sqrt{182}} </math> | |||
Mithilfe des Taschenrechners kann das Ergebnis berechnet werden: | |||
<math> \alpha = sin^{-1}(\frac{1}{\sqrt{182}}) \Leftrightarrow \alpha \approx 21,75 ^\circ </math> | |||
Die Kinder sollten den Strohalm also in einem Winkel von ca. <math> 21,75 ^\circ </math> in das Trinkpäckchen stecken, um an den Saft in der letzten Ecke zu kommen. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode}} | |||
{{Box | Aufgabe <Nummer>: Gerade gesucht | | {{Box | Aufgabe <Nummer>: Gerade gesucht | | ||
Version vom 8. Mai 2021, 19:55 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
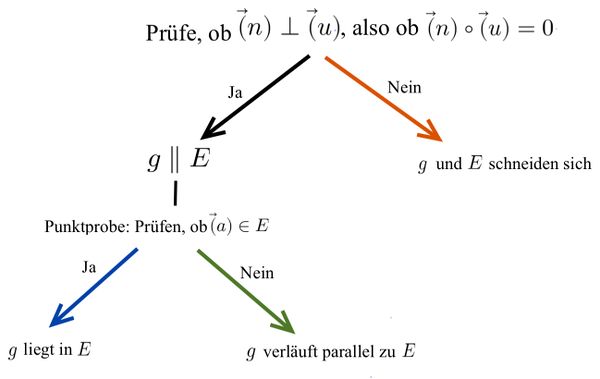
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
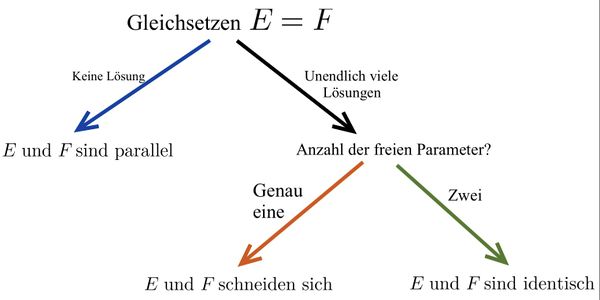
Zwei Ebenengleichungen in Parameterform
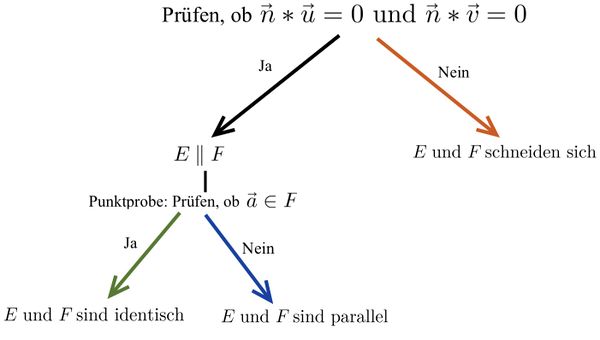
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
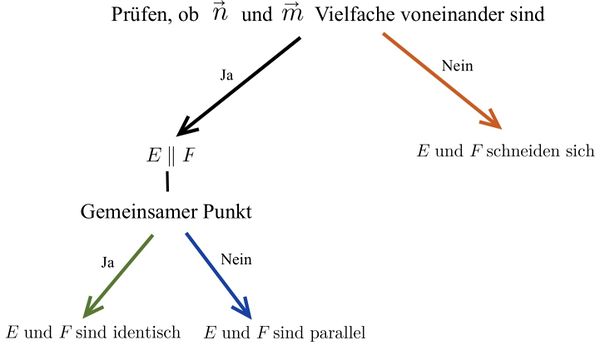
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene