Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 256: | Zeile 256: | ||
==Lagebeziehung Ebene-Ebene== | ==Lagebeziehung Ebene-Ebene== | ||
===Mögliche Lagebeziehungen zwischen zwei Ebenen=== | |||
{{Box|Merke:| | {{Box|Merke:| | ||
Zwischen | Zwischen zwei Ebenen gibt es drei mögliche Lagebeziehungen. | ||
{{3Spalten | {{3Spalten | ||
| | | | ||
| Zeile 284: | Zeile 284: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
===Untersuchung der Lagebeziehung von zwei Ebenen=== | |||
====Zwei Ebenengleichungen in Parameterform==== | |||
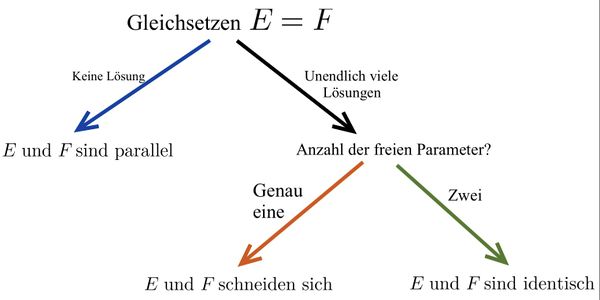
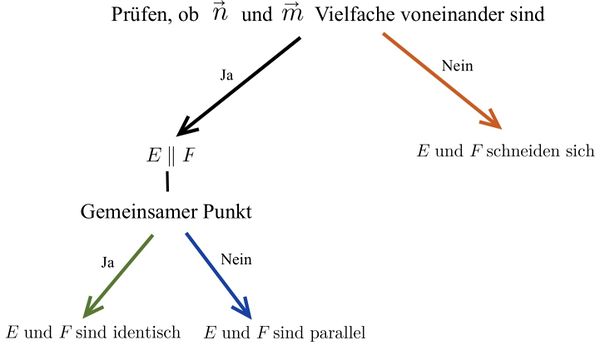
{{Box|Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen. | | {{Box|Merke: Lagebeziehung von zwei Ebenen in Parameterform untersuchen. | | ||
[[Datei:Vorgehen zur Berechnung der Lagebeziehung von Ebenen in Parameterform.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Berechnung der Lagebeziehung von Ebenen in Parameterform.jpg|zentriert|rahmenlos|600x600px]] | ||
| Zeile 326: | Zeile 328: | ||
a) <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | '''a)''' <math>\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, schneiden sich die Ebenen in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da sich in jeder Zeile der Diagonalform Einträge befinden, schneiden sich die Ebenen in einer Schnittgeraden.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
b) <math>\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13 \end{vmatrix}</math> | '''b)''' <math>\begin{vmatrix} 1 & 3 & -2 & 5 & 0 \\ 0 & 7 & -7 & -14 & -2 \\ 0 & 0 & 0 & 0 & -13 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt keine Lösung, da die dritte Zeile nicht lösbar ist. Die Ebenen liegen also parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Das Gleichungssystem besitzt keine Lösung, da die dritte Zeile nicht lösbar ist. Die Ebenen liegen also parallel zueinander.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
c) <math>\begin{vmatrix} 1 & 3 & -2 & -5 & 3 \\ 0 & 7 & -7 & 14 & 7 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}</math> | '''c)''' <math>\begin{vmatrix} 1 & 3 & -2 & -5 & 3 \\ 0 & 7 & -7 & 14 & 7 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}</math> | ||
{{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da die dritte Zeile nur aus Nullen besteht, sind zwei Parameter frei wählbar und die Ebenen identisch.|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Das Gleichungssystem besitzt unendlich viele Lösungen. Da die dritte Zeile nur aus Nullen besteht, sind zwei Parameter frei wählbar und die Ebenen identisch.|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Zeile 340: | Zeile 342: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
====Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform==== | |||
{{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen. | | {{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform und Parameterform untersuchen. | | ||
[[Datei:Vorgehen zur Untersuchung der Lagebeziehung von zwei Ebenen.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Untersuchung der Lagebeziehung von zwei Ebenen.jpg|zentriert|rahmenlos|600x600px]] | ||
| Zeile 387: | Zeile 390: | ||
a) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | '''a)''' <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | ||
b) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | '''b)''' <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | ||
c) <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | '''c)''' <math>E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R} </math> | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
====Zwei Ebenengleichungen in Koordinatenform==== | |||
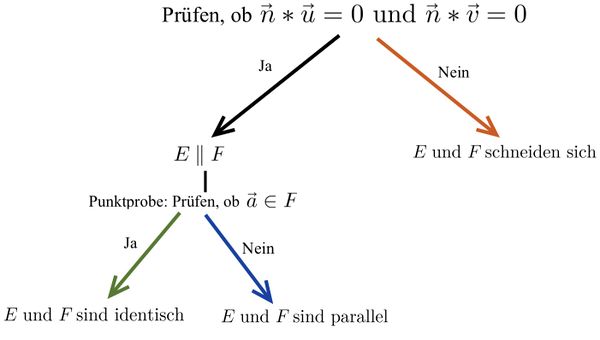
{{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform untersuchen. | | {{Box|Merke: Lagebeziehung von zwei Ebenen in Koordinatenform untersuchen. | | ||
[[Datei:Vorgehen zur Untersuchung der Lagebeziehung von Ebenen in Koordinatenform.jpg|zentriert|rahmenlos|600x600px]] | [[Datei:Vorgehen zur Untersuchung der Lagebeziehung von Ebenen in Koordinatenform.jpg|zentriert|rahmenlos|600x600px]] | ||
| Zeile 421: | Zeile 425: | ||
'''3. Schritt:''' Bestimme die Schnittgerade. | '''3. Schritt:''' Bestimme die Schnittgerade. | ||
Stelle mit den beiden Ebenengleichungen ein LGS auf und löse es mithilfe des Gauß-Algortithmus oder dem Taschenrechner. | |||
<math> \begin{vmatrix} 3 & -4 & -1 & 4 \\ 3 & -3 & 1 & 3 \end{vmatrix} \Leftrightarrow \begin{vmatrix} 3 & -4 & -1 & 4 \\ 0 & 1 & 2 & -1 \end{vmatrix}</math> | |||
Setze <math>x_3=t</math> und bestimme <math>x_1</math> und <math>x_2</math>. | |||
<math>x_2=-1-2t</math> | |||
<math>x_1=-\frac{7}{3}</math> | |||
Stelle die Geradengleichung auf. | |||
<math>g: \vec{x} = \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -\frac{7}{3} \\ -2 \\ 1 \end{pmatrix} </math> | |||
| Zeile 497: | Zeile 515: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Die Normalenvektor der Ebenen < | Die Normalenvektor der Ebenen <math>F</math> und <math>H</math> können abgelesen werden als <math>\vec{m} = \begin{pmatrix} 2 \\ 6 \\ 4 \end{pmatrix} </math> und <math>\vec{l} = \begin{pmatrix} 2 \\ 4 \\ -7 \end{pmatrix} </math> | ||
Einsetzen in die Formel liefert: | Einsetzen in die Formel liefert: | ||
Version vom 8. Mai 2021, 16:33 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
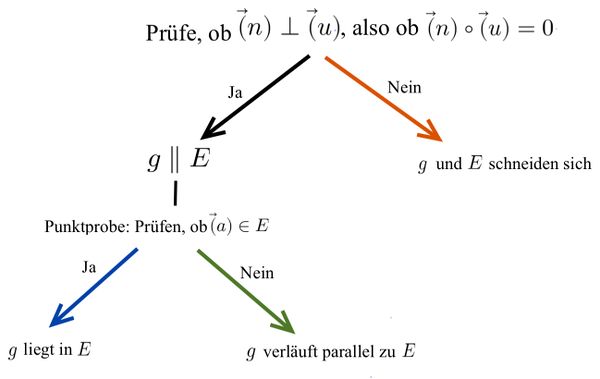
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
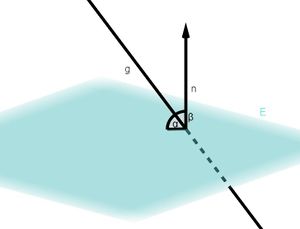
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
Mögliche Lagebeziehungen zwischen zwei Ebenen
Untersuchung der Lagebeziehung von zwei Ebenen
Zwei Ebenengleichungen in Parameterform
Eine Ebenengleichungen in Parameterform – eine Ebenengleichung in Koordinatenform
Zwei Ebenengleichungen in Koordinatenform
⭐Berechnung des Winkels zwischen Ebene und Ebene