Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 452: | Zeile 452: | ||
'''2. Schritt:''' Einsetzen der Normalenvektoren in die Formel. | '''2. Schritt:''' Einsetzen der Normalenvektoren in die Formel. | ||
<math>cos(\alpha) = \frac{ \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \ast \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} \Leftrightarrow cos(\alpha) = \frac{ | <math>cos(\alpha) = \frac{ \begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \ast \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}}{\begin{pmatrix} 2 \\ -2 \\ -1 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 1 \\ -3 \end{pmatrix}} \Leftrightarrow cos(\alpha) = \frac{16}{\sqrt{9} \cdot \sqrt{59}} \Leftrightarrow cos(\alpha) = \frac{16}{3 \cdot \sqrt{59}}</math> | ||
'''3. Schritt:''' Auflösen der Gleichung. | '''3. Schritt:''' Auflösen der Gleichung. | ||
| Zeile 459: | Zeile 459: | ||
{{Box | Aufgabe <Nummer>: Fehlerbeschreibung | | {{Box | Aufgabe <Nummer>: Fehlerbeschreibung | | ||
Sei E eine Ebene mit <math>E: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> , | |||
F eine Ebene mit <math>F: \vec{x} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 3 \\ -6 \end{pmatrix}+ s \cdot \begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> | |||
und H eine Ebene mit <math>H: 7x_1+x_2-3x_3 </math> . | |||
Berechne den Winkel zwischen E und F, F und H und E und H. | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
{{Box | Aufgabe <Nummer>: | | |||
Der Winkel zwischen den beiden Vektoren <math> \vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}</math> und <math> \vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}</math> beträgt <math> 67{,}72 ^{\circ} </math>. | |||
Gib die Gleichungen zweier Ebenen <math>E</math> und <math>F</math> an, die sich in einem Winkel von <math> 67{,}72 ^{\circ} </math> schneiden. | |||
{{Lösung versteckt|1= | |||
Der Winkel zwischen zwei Ebenen entspricht dem Winkel zwischen ihren Normalenvektoren. Da der Winkel zwischen den beiden angebenen Vektoren <math> \vec{a} = \begin{pmatrix} 1\\ 0\\ 3 \end{pmatrix}</math> und <math> \vec{b} = \begin{pmatrix} 4\\ 7\\ 2 \end{pmatrix}</math> genau dem Winkel entspricht, den die Ebenen einschließen sollen, können sie als Normalenvektoren der Ebenen verwendet werden. Die Punkte durch die die Ebenen laufen, können frei gewählt werden. | |||
Eine mögliche Lösung für die Ebenen lautet daher: | |||
<math>E: x_1 + 3x_3 = 4 </math> und <math>F: 4x_1 + 7x_2 + 2x_3 = 8 </math>. | |||
|2=Lösung anzeigen|3=Lösung verbergen}} | |||
| Arbeitsmethode}} | |||
Version vom 8. Mai 2021, 11:22 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
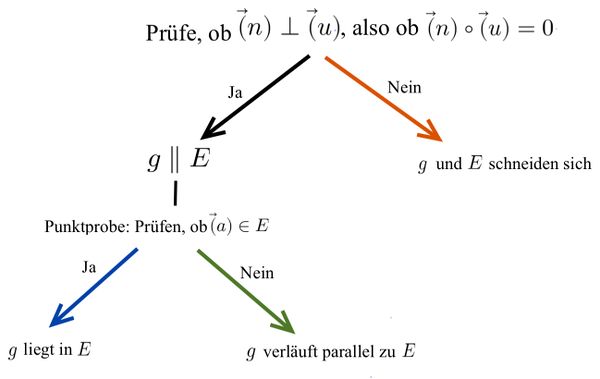
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
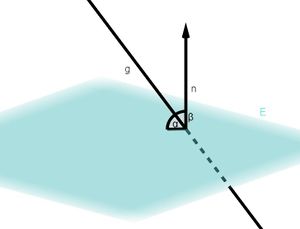
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene