Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Marie (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 105: | Zeile 105: | ||
Berechnung von <math> A' </math>: | Berechnung von <math> A' </math>: | ||
<math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=9-2r \\ y=-5-2r \\ 0=7-10r \end{vmatrix} \Rightarrow x=- | <math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 9\\ -5\\ 7 \end{matrix} \right) + r \cdot \left( \begin{matrix} -2\\ -2\\ -10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=9-2r \\ y=-5-2r \\ 0=7-10r \end{vmatrix} \Rightarrow x=\frac{-63}{5}, y = frac{-32}{5}, r= frac{7}{10} \Rightarrow A'=\left( \begin{matrix} frac{-63}{5}\\ frac{-32}{5}\\ 0 \end{matrix} \right)</math>. | ||
Berechnung von <math> B' </math>: | Berechnung von <math> B' </math>: | ||
<math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=6-2s \\ y=-5-2s \\ 0=7- | <math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 6\\ -5\\ 7 \end{matrix} \right) + s \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=6-2s \\ y=-5-2s \\ 0=7-10s \end{vmatrix} \Rightarrow x=\frac{-42}{5}, y = \frac{-32}{5}, r= \frac{7}{10} \Rightarrow B'=\left( \begin{matrix} \frac{-42}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right)</math>. | ||
Berechnung von <math> C' </math>: | Berechnung von <math> C' </math>: | ||
<math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=7- | <math>\left( \begin{matrix} x\\ y\\ 0 \end{matrix} \right)=\left( \begin{matrix} 7\\ -10\\ 11 \end{matrix} \right) + t \cdot \left( \begin{matrix} -2\\ -2\\ 10 \end{matrix} \right) \Rightarrow \begin{vmatrix} x=7-2t \\ y=-10-2t \\ 0=11-10t \end{vmatrix} \Rightarrow x=\frac{-77}{5}, y = \frac{-61}{5}, t= \frac{11}{10} \Rightarrow C'=\left( \begin{matrix} \frac{-77}{5}\\ \frac{-61}{5}\\ 0 \end{matrix} \right)</math>. | ||
Die Schattenfläche wird also durch das Dreieck mit den Eckpunkten <math> A'=\left( \begin{matrix} - | Die Schattenfläche wird also durch das Dreieck mit den Eckpunkten <math> A'=\left( \begin{matrix} frac{-63}{5}\\ frac{-32}{5}\\ 0 \end{matrix} \right), B'=\left( \begin{matrix} \frac{-42}{5}\\ \frac{-32}{5}\\ 0 \end{matrix} \right) </math> und <math> C'=\left( \begin{matrix} \frac{-77}{5}\\ \frac{-61}{5}\\ 0 \end{matrix} \right)</math> begrenzt. | ||
|2= Lösung anzeigen| 3= Lösung verbergen}} | |2= Lösung anzeigen| 3= Lösung verbergen}} | ||
| Zeile 193: | Zeile 193: | ||
{{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem die die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | {{Lösung versteckt|1= Berechne den Schnittpunkt der Gerade mit der Ebene, indem die die einzelnen Koordinaten der Gerade in die Ebenengleichung einsetzt.|2=Tipp anzeigen|3=Tipp verbergen}} | ||
{{Lösung versteckt|1= <math> -5 + 2s + 3(\frac{3}{2} + \frac{1}{2}s) = 2 \Leftrightarrow s \approx 0,71 </math> | {{Lösung versteckt|1= <math> -5 + 2s + 3(\frac{3}{2} + \frac{1}{2}s) = 2 \Leftrightarrow s \approx 0,71 </math> | ||
Berechne den Schnittpunkt, indem du s in die Geradengleichung einsetzt: <math>\left( \begin{matrix} 7\\ {-}5\\ | Berechne den Schnittpunkt, indem du s in die Geradengleichung einsetzt: <math>\left( \begin{matrix} 7\\ {-}5\\ \frac{3}{2} \end{matrix} \right) + 0,71 \cdot \left( \begin{matrix} 1\\ 2\\ \frac{1}{2} \end{matrix} \right) \approx \left( \begin{matrix} 7,71\\ -3,58\\ 1,86 \end{matrix} \right)</math>|2=Lösung anzeigen|3=Lösung verbergen}} | ||
| Arbeitsmethode | Farbe={{Farbe|orange}}}} | | Arbeitsmethode | Farbe={{Farbe|orange}}}} | ||
Version vom 8. Mai 2021, 10:00 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
Lagebeziehung Gerade-Ebene
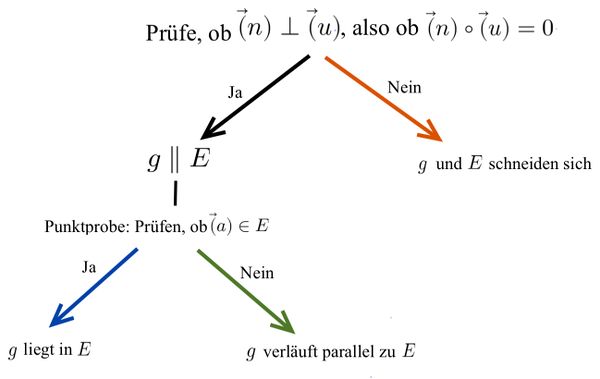
Mögliche Lagebeziehungen zwischen Gerade und Ebene
Untersuchung der Lagebeziehung zwischen Gerade und Ebene
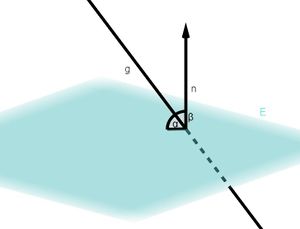
⭐Berechnung des Winkels zwischen Gerade und Ebene
Lagebeziehung Ebene-Ebene
⭐Berechnung des Winkels zwischen Ebene und Ebene