Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 16: | Zeile 16: | ||
==Einstieg== | ==Einstieg== | ||
1. Zwei Kinder befinden sich im Klettergarten auf zwei verschiedenen Seilen. Wo auf ihrem Seil müssen sie sein, damit sie sich am nächsten sind? Wie nah sind sie sich dann? | |||
A.<math>G(4|-10|19)</math> ist der Lotfußpunkt auf <math>g</math> und <math>H(-2|-12|22)</math> ist der Lotfußpunkt auf <math>g</math>. Der Abstand ist dann <math>d(g;h)=d(G;H)=\sqrt{(4-(-2))^2+(-10-(-12))^2+(22-19)^2}=\sqrt{36+4+9}=7</math>. | |||
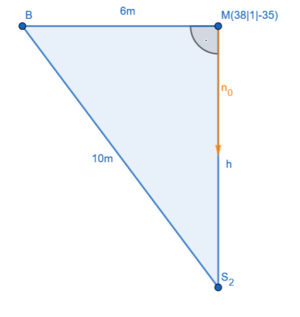
2. Bei einem alten Haus soll bei der Renovierung ein Stützbalken vom Boden im Dachgeschoss zur oberen Dachkante gebaut werden. Er soll senkrecht auf dem Fußboden stehen. Wie lang muss er sein? | |||
B. <math>h:\vec{x}=\begin{pmatrix} 2 \\ 0 \\ 15 \end{pmatrix}+s\cdot\begin{pmatrix} 0 \\ 0 \\ -3 \end</math> ist die zu <math>E: x_3=10</math> orthogonale Gerade durch einen Punkt von <math>g</math>. Wegen <math>15-3s=10</math>, also <math>s=\frac{5}{3}</math>, erhält man den Lotfußpunkt <math>(2|0|10)</math>. | |||
3.Luke Skywalker fliegt in seinem Raumschiff zum Auskundschaften am Todesstern vorbei. Dieser befindet sich im Verhältnis zur geradlinigen Bewegung des Raumschiffs in Ruhe. Der Sensor auf dem Todesstern hat eine Reichweite von <math>10km</math>. Wird Luke mit seinem Raumschiff entdeckt? | |||
==Abstand eines Punktes von einer Ebene== | ==Abstand eines Punktes von einer Ebene== | ||
Version vom 6. Mai 2021, 19:53 Uhr
Einstieg
1. Zwei Kinder befinden sich im Klettergarten auf zwei verschiedenen Seilen. Wo auf ihrem Seil müssen sie sein, damit sie sich am nächsten sind? Wie nah sind sie sich dann?
A. ist der Lotfußpunkt auf und ist der Lotfußpunkt auf . Der Abstand ist dann .
2. Bei einem alten Haus soll bei der Renovierung ein Stützbalken vom Boden im Dachgeschoss zur oberen Dachkante gebaut werden. Er soll senkrecht auf dem Fußboden stehen. Wie lang muss er sein?
B. Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle h:\vec{x}=\begin{pmatrix} 2 \\ 0 \\ 15 \end{pmatrix}+s\cdot\begin{pmatrix} 0 \\ 0 \\ -3 \end} ist die zu orthogonale Gerade durch einen Punkt von . Wegen , also , erhält man den Lotfußpunkt .
3.Luke Skywalker fliegt in seinem Raumschiff zum Auskundschaften am Todesstern vorbei. Dieser befindet sich im Verhältnis zur geradlinigen Bewegung des Raumschiffs in Ruhe. Der Sensor auf dem Todesstern hat eine Reichweite von . Wird Luke mit seinem Raumschiff entdeckt?
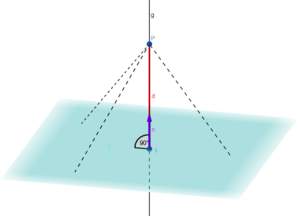
Abstand eines Punktes von einer Ebene
Das Lotfußpunktverfahren
Die Hesse´sche Normalenform
Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotverfahren auch die Möglichkeit, dies mit der Hesse´schen Normalenform zu berechnen. In diesem Abschnitt lernst du, wie du die Normalenform aufstellst und sie zur Abstandsberechnung anwendest.
Falls du noch nicht genug hast, kannst du auch versuchen, die Aufgaben vom Lotfußpunktverfahren mit der Hesse´schen Normalenform zu lösen.
Abstand eines Punktes von einer Geraden
Abstand zweier windschiefer Geraden
Verschiebe die Punkte und so, dass die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden und ist. Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten.

Gemischte Aufgaben
- auf Anfangsaufgabe zurückkommen
- 3 Aufgaben