Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 230: | Zeile 230: | ||
{{Box | Aufgabe <Nummer>: Bank am Wanderweg | | {{Box | Aufgabe <Nummer>: Bank am Wanderweg | | ||
An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene <math> S_1: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0,4 \\ 0\end{pmatrix}, r,s \in \mathbb{R} </math> und die Rückenlehne durch die Ebene | An einem Wanderweg soll eine Holzbank aufgestellt werden. Die Bank wird so ausgerichtet, dass die Sitzfläche durch die Ebene <math> S_1: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0,4 \\ 0\end{pmatrix}, r,s \in \mathbb{R} </math> und die Rückenlehne durch die Ebene <math>R_1: -x_2 + 0,4 x_3 = -0,2 </math> beschrieben werden kann. | ||
'''a)''' Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob die auf die neue Bank zutrifft. | '''a)''' Um eine bequeme Sitzposition zu ermöglichen, sollte der Winkel zwischen Rückenlehne und Sitzfläche zwischen 100 und 110 liegen. Überprüfe, ob die auf die neue Bank zutrifft. | ||
| Zeile 247: | Zeile 247: | ||
[[Datei:Winkel zwischen zwei Ebenen (Bankaufgabe).png|mini|Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank]] | [[Datei:Winkel zwischen zwei Ebenen (Bankaufgabe).png|mini|Skizze: Winkel zwischen der Rückenlehne und der Sitzfläche der Bank]] | ||
Wie in Abbildung ... zu sehen wurde der Winkel <math> \gamma </math> berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel <math> \alpha </math> beschrieben. <math>\ | Wie in Abbildung ... zu sehen wurde der Winkel <math> \gamma </math> berechnet. Der Winkel zwischen der Sitzfläche und der Rückenlehne wird aber durch den Winkel <math> \alpha </math> beschrieben. <math>\alpha</math> erhält man, indem man <math>180 ^\circ - \gamma </math> berechnet: <math>180 ^\circ - 68,2 ^\circ = 111,8 ^\circ </math>. Mit einem Wert von <math> 111,8 ^\circ </math> liegt der Winkel zwischen Rückenlehne und Sitzfläche etwas über dem optimalen Winkel. |2=Lösung anzeigen|3=Lösung verbergen}} | ||
'''b)''' Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene <math> S_2: \vec{x} = \begin{pmatrix} 0 \\ 0,8 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0,4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> und die Rückenlehne der Ebene <math> R_2: -x_2 - 0,4 x_3 = -1 </math> Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen. | '''b)''' Da der Wanderweg sehr beliebt ist, soll noch eine zweite Bank aufgestellt werden. Sie wird so ausgerichtet, dass beide Bänke mit den Rückenlehnen aneinander stehen. Auch bei der zweiten Bank können die Sitzfläche und die Rückenlehne durch Ebenen beschrieben werden. Die Sitzfläche entspricht der Ebene <math> S_2: \vec{x} = \begin{pmatrix} 0 \\ 0,8 \\ 0,5 \end{pmatrix} + r \cdot \begin{pmatrix} 0 \\ 0,4 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 2 \\ 0 \\ 0\end{pmatrix}, r,s \in \mathbb{R}</math> und die Rückenlehne der Ebene <math> R_2: -x_2 - 0,4 x_3 = -1 </math> Berechne den Winkel, unter dem die beiden Rückenlehnen der Bänke aufeinander treffen. | ||
Version vom 6. Mai 2021, 16:28 Uhr
Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
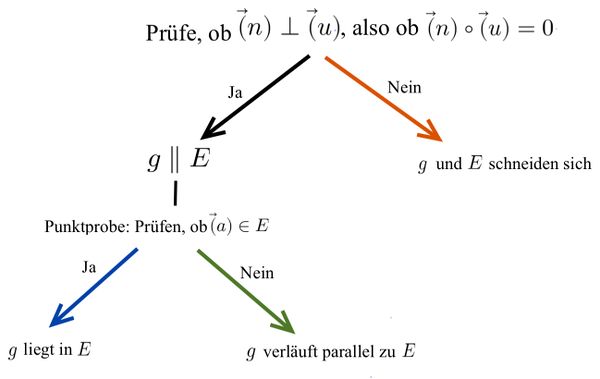
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
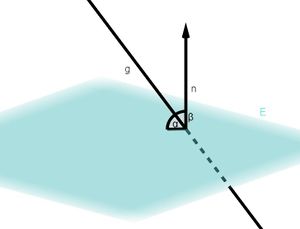
⭐Berechnung des Winkels zwischen Gerade und Ebene
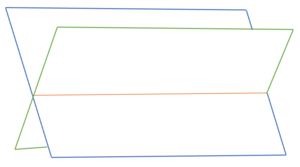
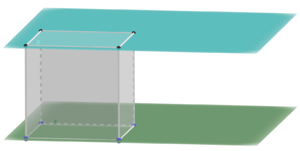
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene