Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen): Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 88: | Zeile 88: | ||
===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ===⭐Berechnung des Winkels zwischen Gerade und Ebene=== | ||
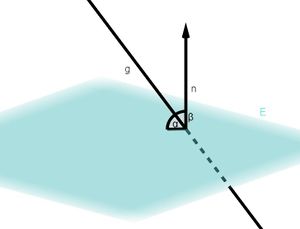
[[Datei:Abbildung- Winkel zwischen Gerade und Ebene.jpg|mini | [[Datei:Abbildung- Winkel zwischen Gerade und Ebene.jpg|mini|Abbildung: Winkel zwischen Gerade und Ebene]] | ||
{{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>n</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>u</math>. Der Schnittwinkel <math>\beta</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math> sin(\beta)=\frac{ n \ast u}{|n| \cdot |u|}</math> | Merksatz}} | {{Box | Merksatz: Winkel berechnen zwischen Gerade und Ebene | Sei <math>E</math> eine Ebene mit dem Normalenvektor <math>n</math> und <math>g</math> eine Gerade mit dem Richtungsvektor <math>u</math>. Der Schnittwinkel <math>\beta</math> zwischen <math>E</math> und <math>g</math> kann mit folgender Formel berechnet werden: <math> sin(\beta)=\frac{ n \ast u}{|n| \cdot |u|}</math> | Merksatz}} | ||
| Zeile 119: | Zeile 113: | ||
Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\left( \begin{matrix} 3\\ 6\\ z \end{matrix} \right)</math> verläuft. Stelle die Gerade <math>g</math> auf. | Eine Gerade <math>g</math> soll die <math>x_1-x_2-Ebene </math> in einem Winkel von <math>45</math> schneiden. Über die Gerade <math>g</math> ist nur bekannt, dass sie im Punkt <math>P (1|2|3) </math> beginnt und sie in Richtung des Vektors <math>\vec{x}=\left( \begin{matrix} 3\\ 6\\ z \end{matrix} \right)</math> verläuft. Stelle die Gerade <math>g</math> auf. | ||
{{Lösung versteckt|1=Tipp 1 anzeigen|2=Inhalt|3=Tipp 1 verbergen}} | |||
{{Lösung versteckt|1=Tipp 2 anzeigen|2=Inhalt|3=Tipp 2 verbergen}} | |||
{{Lösung versteckt|1=Lösung anzeigen|2=Lösung|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
Version vom 5. Mai 2021, 19:33 Uhr
dHier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".
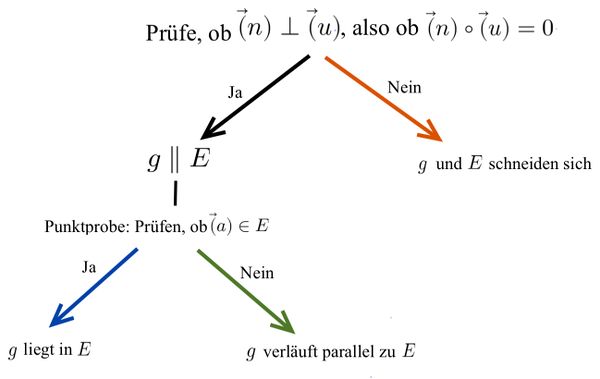
Lagebeziehung Gerade-Ebene
Mögliche Lagebeziehungen zwischen Gerade und Ebene
⭐Berechnung des Winkels zwischen Gerade und Ebene
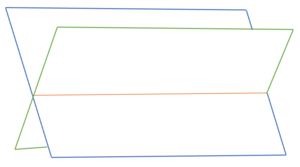
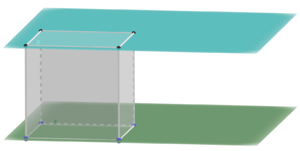
Lagebeziehung Ebene-Ebene
Basiswissen
⭐Berechnung des Winkels zwischen Ebene und Ebene