Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)

Hier entsteht das Lernpfadkapitel "Lagebeziehungen und Winkel (Gerade und Ebene, 2 Ebenen)".

Info

In diesem Lernpfadkapitel <Kurzbeschreibung des Kapitelziels>

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
• Aufgaben und Kapitel, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht.

Viel Erfolg!

Lagebeziehung Gerade-Ebene

Mögliche Lagebeziehungen zwischen Gerade und Ebene

Aufgabe: Lückentext zur Lagebeziehung zwischen Gerade und Ebene

Beispielaufgabe: Untersuchung der Lagebeziehung von Gerade und Ebene

Gegeben sind eine Ebene $E: \vec{x} = \left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right), s,t  \in \mathbb{R}$ und eine Gerade $g: \vec{x} = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right), r  \in \mathbb{R}$. Untersuche die Lagebeziehung der Gerade und der Ebene und bestimme gegebenenfalls den Schnittpunkt.

1. Schritt: Setze die Geraden- und Ebenengleichung gleich.

$\left( \begin{matrix} 1\\ 0\\ 0 \end{matrix} \right) + s \cdot \left( \begin{matrix} -1\\ 1\\ 0 \end{matrix} \right) + t \cdot \left( \begin{matrix} -1\\ 0\\ 1 \end{matrix} \right) = \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + r \cdot \left( \begin{matrix} -1\\ -4\\ t=2 \end{matrix} \right)$

2. Schritt: Stelle das zugehörige lineare Gleichungssystem auf.

$\begin{vmatrix} 1-s-t=2-r \\ s=2-4r \\ 0=0 \end{vmatrix}$

3. Schritt: Löse das Gleichungssystem mit dem Gaußverfahren oder dem Taschenrechner.

$s=-1, t=2, r=1$

4. Schritt: Interpretiere die Lösung des Gleichungssystems anhand der Anzahl der Lösungen.

Da das Gleichungssystem nur eine Lösung hat, besitzen die Ebene $E$ und die Gerade $g$ nur einen gemeinsamen Punkt. Also schneidet die Gerade die Ebene.

5. Schritt: Da sich die Ebene $E$ und die Gerade $g$ schneiden, kannst du den Schnittpunkt der beiden berechnen. Setze dafür den Parameter $r$ in die Geradengleichung ein.

$g: \left( \begin{matrix} 2\\ 2\\ 2 \end{matrix} \right) + 1 \cdot \left( \begin{matrix} -1\\ -4\\ 0 \end{matrix} \right) = \left( \begin{matrix} 1\\ -2\\ 2 \end{matrix} \right)$

Für die Lage einer Gerade g zu einer Ebene E sind 3 Fälle möglich:

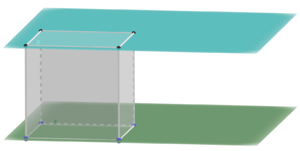
• Die Gerade g liegt in der Ebene E.
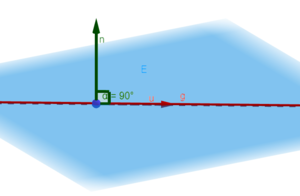
• Die Gerade g liegt parallel zur Ebene E. 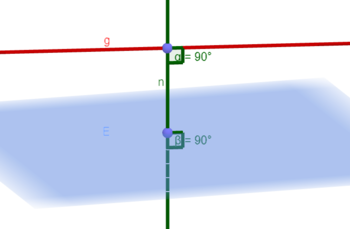Die Gerade g und die Ebene E schneiden sich.

Untersuchung der Lagebeziehung

Vorgehen

Beispiel (Ebene in Parameterform)

Übungsaufgaben (Learning App)

Beispiel (Ebene in Koordinatenform)

Übungsaufgaben

⭐Berechnung des Winkels zwischen Gerade und Ebene

Merke: Winkel berechnen zwischen Gerade und Ebene

Wenn sich eine Ebene und eine Gerade schneiden, kann nicht nur der Schnittpunkt, sondern auch der Schnittwinkel bestimmt werden. Wie in Abbildung ... zu sehen ist, wird dafür der Normalenvektor der Ebene und der Richtungsvektor der Gerade betrachtet.

Um den Schnittwinkel zu berechnen, musst du zunächst den Normalenvektor der Ebene bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum

Merksatz: Winkel berechnen zwischen Gerade und Ebene

Sei $E$ eine Ebene mit dem Normalenvektor $n$ und $g$ eine Gerade mit dem Richtungsvektor $u$. Der Schnittwinkel $\alpha$ zwischen $E$ und $g$ kann mit folgender Formel berechnet werden: $sin(\alpha)=\frac{ n \ast u}{|n| \cdot |u|}$

Beispiel: Winkel berechnen zwischen Gerade und Ebene

Inhalt

Aufgabe <Nummer>: <Name>

Inhalt

Aufgabe <Nummer>: Winkel gesucht

Inhalt

Lagebeziehung Ebene-Ebene

Basiswissen

Aufgabe: Lückentext zur Lagebeziehung zwischen Ebene und Ebene

Untersuchung der Lagebeziehung zwischen zwei Ebenen

Seien E und F zwei Ebenen im Raum. Um die Lagebeziehung dieser Ebenen zu untersuchen, müssen eine Reihe bestimmter Rechenschritte durchgeführt werden:

Schritt 1: Die beiden Ebenengleichungen gleichsetzen

Schritt 2: LGS interpretieren

Schritt 3: Schnittgerade bestimmen

Aufgabe: Ergebnisse interpretieren

Interpretiere die jeweilige Situation geometrisch.

a) $\begin{vmatrix} 1 & 0 & 0 & -0,5 & 0,5 \\ 0 & 1 & 0 & -1 & 0,5 \\ 0 & 0 & 1 & 1,5 & 1 \end{vmatrix}$

b) $\begin{vmatrix} 1 & 0 & -1 & -2 & 0 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{vmatrix}$

c) $\begin{vmatrix} 1 & 0 & -1 & -2 & 1 \\ 0 & 1 & -1 & -3 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{vmatrix}$

Aufgabe: Lagebeziehungen berechnen

Untersuche die Lagebeziehung der jeweiligen Ebenen.

a) $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

b) $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

c) $E: \vec{x} = \begin{pmatrix} 0 \\ 0 \\ 2{,}5 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ 0 \\ -2 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 1 \\ -1{,}5 \end{pmatrix}, t,s \in \mathbb{R}$

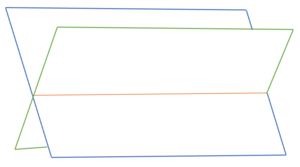
Aufgabe: Schnitt von zwei Zeltflächen

Die beiden Seitenflächen eines Zeltes liegen in den Ebenen $E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}, r,s \in \mathbb{R}$ und $E: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}, t,u \in \mathbb{R}$. Berechne die Geradengleichung der oberen Zeltkante.

⭐Berechnung des Winkels zwischen Ebene und Ebene

Merke: Winkel berechnen zwischen zwei Ebenen

Wenn sich zwei Ebenen schneiden, kann der Schnittwinkel bestimmt werden, den sie einschließen. Wie in Abbildung ... zu sehen ist, kannst du dazu die Normalenvektoren betrachten. Sie schließen denselben Winkel ein, wie die beiden Ebenen. Betrachten wir die Normalenvektoren, so können wir ähnlich vorgehen, wie beim Berechnen des Winkels zwischen zwei Geraden.

Um den Schnittwinkel zu berechnen, musst du zunächst die Normalenvektoren der Ebenen bestimmen. Wenn du nicht mehr genau weißt, wie das geht, schaue nochmal in Kapitel Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Ebenen im Raum

Merksatz: <Name>

Seien $E$ und $F$ zwei sich schneidende Ebenen mit den Normalenvektoren $n$ und $m$. Der Schnittwinkel $\alpha$ zwischen $E$ und $F$ kann mit folgender Formel berechnet werden: $cos(\alpha)=\frac{ n \ast m}{|n| \cdot |m|}$

Beispiel: Winkel berechnen zwischen zwei Ebenen

Inhalt

Aufgabe <Nummer>: Fehlerbeschreibung

Inhalt

Aufgabe <Nummer>: Zeltwände

Wir betrachten noch einmal die Situation aus Aufgabe ...: Die beiden Seitenflächen eines Zeltes liegen in den Ebenen $E: \vec{x} = \begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} + r \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ s \cdot \begin{pmatrix} 0 \\ 3 \\ 4\end{pmatrix}, r,s \in \mathbb{R}$ und $E: \vec{x} = \begin{pmatrix} 8 \\ 6 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}+ u \cdot \begin{pmatrix} 0 \\ -3 \\ 4 \end{pmatrix}, t,u \in \mathbb{R}$. a) Berechne den Winkel, unter dem sich die Seitenflächen treffen.

b) Berechne den Außenwinkel der Zeltwand zum Boden, wenn diese durch die $x_1-x_2$-Ebene dargestellt wird.