Herta-Lebenstein-Realschule/Lernpfad Geometrie/5) Symmetrie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (S.112, Nr. 19 Lösung + Tipp) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 103: | Zeile 103: | ||
|2=Tipp zu Nr. 3|3=Tipp ausblenden}} | |2=Tipp zu Nr. 3|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= [[Datei:S.109, Nr. 3 Lösung.jpg|200px]] | {{Lösung versteckt|1= [[Datei:S.109, Nr. 3 Lösung.jpg|200px]] | ||
|2=Lösung zu Nr. 3|3= | |2=Lösung zu Nr. 3|3=Lösung ausblenden}} | ||
<br> | <br> | ||
{{Lösung versteckt|1= <br> | {{Lösung versteckt|1= <br> | ||
| Zeile 113: | Zeile 113: | ||
|2=Tipp zu Nr. 5|3=Tipp ausblenden}} | |2=Tipp zu Nr. 5|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=[[Datei:Lösung S.109, Nr. 5.jpg|600px]] | {{Lösung versteckt|1=[[Datei:Lösung S.109, Nr. 5.jpg|600px]] | ||
|2=Lösung zu Nr. 5|3= | |2=Lösung zu Nr. 5|3=Lösung ausblenden}} | ||
<br> | <br> | ||
{{Lösung versteckt|1= <br> | {{Lösung versteckt|1= <br> | ||
| Zeile 122: | Zeile 122: | ||
|2=Tipp zu Nr. 18|3=Tipp ausblenden}} | |2=Tipp zu Nr. 18|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=[[Datei:S.111, Nr. 18 Lösung.jpg|400px]] | {{Lösung versteckt|1=[[Datei:S.111, Nr. 18 Lösung.jpg|400px]] | ||
|2=Lösung zu Nr. 18|3= | |2=Lösung zu Nr. 18|3=Lösung ausblenden}} | ||
<br> | <br> | ||
{{Lösung versteckt|1= <br> | {{Lösung versteckt|1= <br> | ||
| Zeile 129: | Zeile 129: | ||
# Verbinde anschließend die Bildpunkte so, wie auch die Punkte links von der Spiegelachse miteinander verbunden sind. | # Verbinde anschließend die Bildpunkte so, wie auch die Punkte links von der Spiegelachse miteinander verbunden sind. | ||
|2=Tipp zu Nr. 19|3=Tipp ausblenden}} | |2=Tipp zu Nr. 19|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1=[[Datei:S.112, Nr. 19 Lösung.jpg| | {{Lösung versteckt|1=<br>[[Datei:S.112, Nr. 19 Lösung.jpg|200px]] | ||
|2=Lösung zu Nr. 19|3= | |2=Lösung zu Nr. 19|3=Lösung ausblenden}} | ||
Version vom 11. Februar 2021, 14:22 Uhr
5. Symmetrie
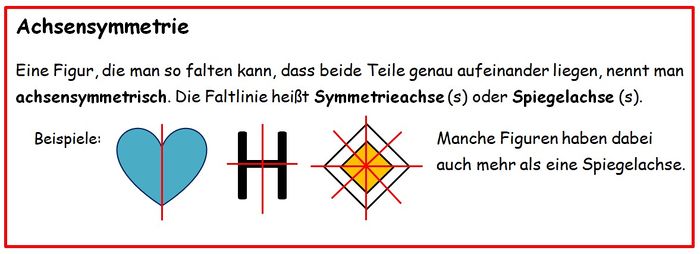
5.1 Achsensymmetrie


noch ergänzen
noch ergänzen
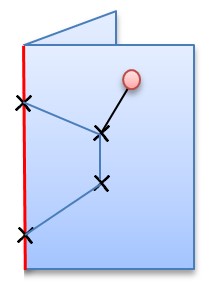
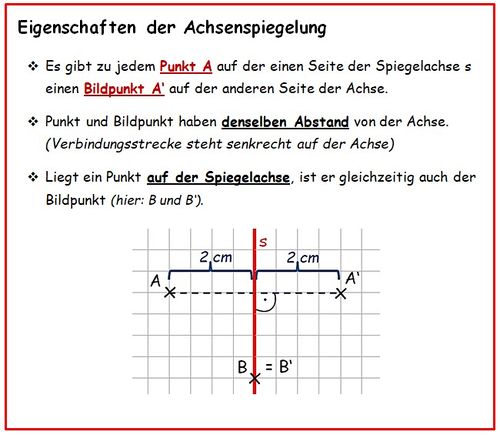
5.2 Achsenspiegelung
Apfel

Schmetterling


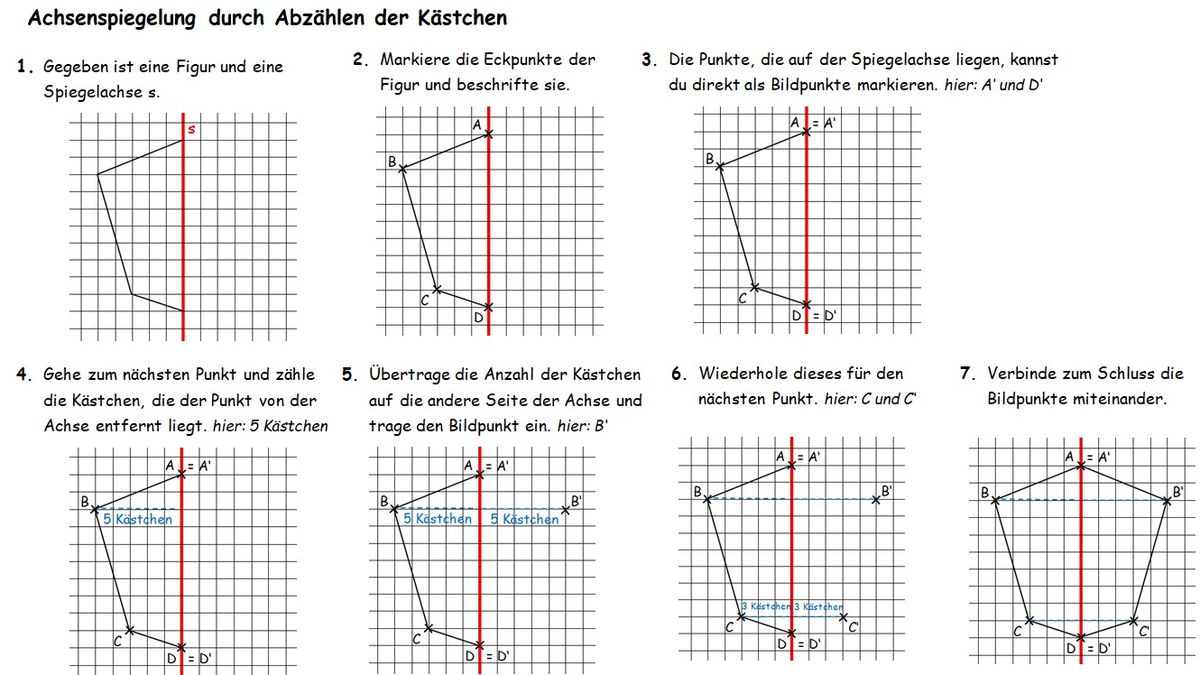
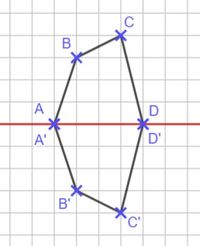
- Markiere die Eckpunkte der Figur. Es gibt insgesamt 4 (2 davon liegen auf der Symmetrieachse).
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen nach unten. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte.
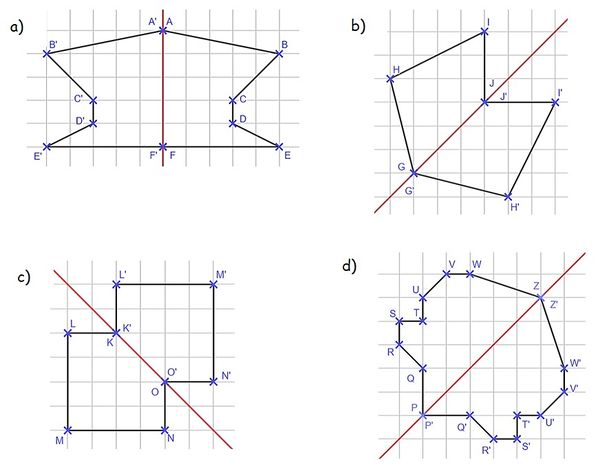
- Markiere die Eckpunkte der Figur. Bei a) gibt es insgesamt 6, bei b) 4, bei c) 5 und bei d) 9 Eckpunkte. Bei allen liegen immer 2 davon auf der Spiegelachse.
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage diesen auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
Bei b) - c) verläuft die Spiegelachse schräg. Hier empfiehlt sich die Methode mit dem Geodreieck.
- Verbinde anschließend die Bildpunkte.
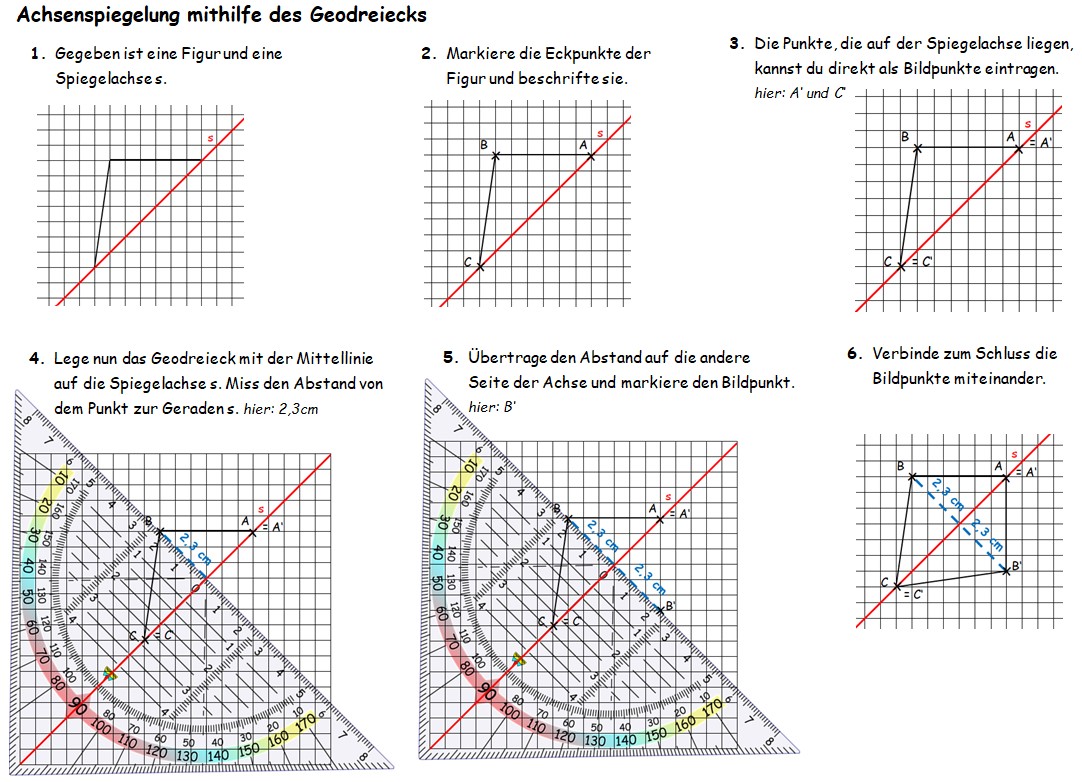
- Markiere die Eckpunkte der Figur. Es gibt insgesamt 7 Eckpunkte (2 davon liegen auf der Spiegelachse).
- Die beiden Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben. Lege hierfür dein Geodreieck mit der Mittellinie auf die Spiegelachse und übertrage den gemessenen Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte.
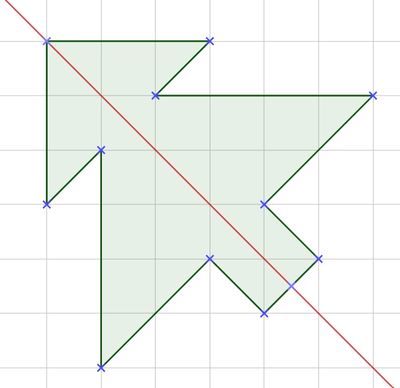
- Die drei Punkte, die auf der Spiegelachse liegen, kannst du direkt als Bildpunkte beschriften.
- Miss bei den anderen beiden Punkten den Abstand, den sie von der Symmetrieachse haben und übertrage den Abstand auf die andere Seite der Spiegelachse. Markiere die Bildpunkte.
- Verbinde anschließend die Bildpunkte so, wie auch die Punkte links von der Spiegelachse miteinander verbunden sind.
5.3 Achsenspiegelung im Koordinatensystem
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 7cm, y-Achse: 6cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C, D und P ein.
- Zeichne nun die Symmetrieachse ein. Sie soll parallel zur x-Achse verlaufen und durch den Punkt P gehen. Lege dein Geodreieck mit den parallelen Hilfslinien auf die x-Achse und schiebe es soweit hoch, dass die Zeichenkante durch den Punkt P geht. Zeichne nun die parallele Gerade ein.
- Spiegle die Punkte an der Symmetrieachse und notiere die Koordinaten.
- Zeichne ein Koordinatensystem in dein Heft (x-Achse: 4cm, y-Achse: 5cm; 2 Kästchen entsprechen einer Einheit) und trage die Punkte A, B, C und D ein.
- Zeichne nun die Symmetrieachse ein, indem du eine Gerade durch die Punkte A und B zeichnest.
- Spiegle die Punkte an der Symmetrieachse.
Kontrolliere die Koordinaten der Bildpunkte: 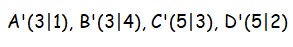
Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen.
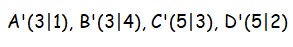
Denke daran, dass bei dir das Koordinatensystem und die Figur im Heft gezeichnet sein müssen.