Digitale Werkzeuge in der Schule/Basiswissen Analysis/Optimierungsprobleme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 139: | Zeile 139: | ||
| | | | ||
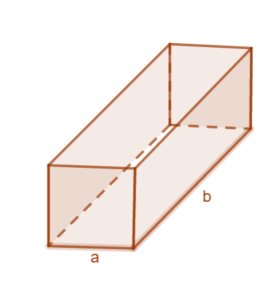
Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen (<math>a</math>) her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein: | Eine Kartonfabrik stellt quaderförmige Pakete mit quadratischen Seitenflächen (<math>a</math>) her. Damit die Pakete nicht zu unhandlich werden, sollen noch zwei Bedingungen erfüllt sein: | ||
* Die Länge (<math>b</math>) soll nicht größer als <math> | * Die Länge (<math>b</math>) soll nicht größer als <math> 200</math>cm sein. | ||
* Länge (<math>b</math>) plus Umfang einer quadratischen Seitenfläche soll <math> | * Länge (<math>b</math>) plus Umfang einer quadratischen Seitenfläche soll <math> 360</math>cm groß sein. [[Datei:Kartonfabrik 3.png|300|rechts|rahmenlos]] | ||
'''a)''' Ermittle die Abmessungen des Pakets mit dem größten Volumen. | '''a)''' Ermittle die Abmessungen des Pakets mit dem größten Volumen. | ||
{{Lösung versteckt | 1= | {{Lösung versteckt | 1= | ||
| Zeile 152: | Zeile 150: | ||
Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach <math>b</math> um. | Nutze die zweite Bedingung, stelle eine Gleichung auf und stelle diese nach <math>b</math> um. | ||
Zweite Bedingung: Länge (<math>b</math>) plus Umfang '''einer''' quadratischen Seitenfläche soll <math> | Zweite Bedingung: Länge (<math>b</math>) plus Umfang '''einer''' quadratischen Seitenfläche soll <math> 360</math>cm groß sein. Den Umfang einer quadratischen Seitenfläche erhältst du, indem du <math>4*a</math> rechnest. | ||
| 2=Tipp für eine geeignete Nebenbedingung | 3=Tipp verbergen}} | | 2=Tipp für eine geeignete Nebenbedingung | 3=Tipp verbergen}} | ||
| Zeile 161: | Zeile 159: | ||
<math>200</math><math>\geq</math><math>360-4*a</math>. | <math>200</math><math>\geq</math><math>360-4*a</math>. | ||
| 2= Tipp zur Bestimmung der Definitionsmenge | 3= Tipp verbergen }} | | 2= Tipp zur Bestimmung der Definitionsmenge | 3= Tipp verbergen }} | ||
'''b)''' Gebe das maximale Volumen an. | |||
{{Lösung versteckt | 1= | |||
Um das maximale Volumen angeben zu können, nutze die in Aufgabenteil a ermittelten Abmessungen für die Höhe, Breite und Länge. Das Volumen errechnest du, indem durch Höhe <math>* </math>Breite <math>*</math> Länge rechnest. |Tipp zur Errechnung des Volumens | Tipp verbergen }} | |||
{{Lösung versteckt | 1= | {{Lösung versteckt | 1= | ||
| Zeile 176: | Zeile 181: | ||
<math>360 - 4*a \geq 0</math>. | <math>360 - 4*a \geq 0</math>. | ||
Durch das Umstellen nach <math>a</math> folgt:<math>a \leq 90</math>. | Durch das Umstellen nach <math>a</math> folgt:<math>a \leq 90</math>. | ||
Außerdem muss die Länger kleiner gleich <math>200 | Außerdem muss die Länger kleiner gleich <math>200</math>cm sein. Es gilt also: | ||
<<math>360 - 4*a \leq 200</math>. | <<math>360 - 4*a \leq 200</math>. | ||
Durch das Umstellen nach <math>a</math> folgt: <math>a \geq 40</math>. | Durch das Umstellen nach <math>a</math> folgt: <math>a \geq 40</math>. | ||
| Zeile 197: | Zeile 202: | ||
Durch das Einsetzen von <math> a = 60 </math> in <math>V''(a)</math> folgt, dass <math>V(a)</math> an dieser Stelle einen Hochpunkt besitzt. | Durch das Einsetzen von <math> a = 60 </math> in <math>V''(a)</math> folgt, dass <math>V(a)</math> an dieser Stelle einen Hochpunkt besitzt. | ||
Breite und Höhe sind also <math>60 | Breite und Höhe sind also <math>60</math>cm. | ||
Die Länge ergibt sich durch das einsetzen von <math> a = 60</math> in <math> b = 360 - 4*a</math>. | Die Länge ergibt sich durch das einsetzen von <math> a = 60</math> in <math> b = 360 - 4*a</math>. | ||
<math> b = 120 | <math> b = 120</math>cm. | ||
'''Das Volumen bestimmen''': Wir berechnen nun das Volumen des optimalen Paketes, indem wir <math>60 * 60 * 120 </math> berechnen. | '''Das Volumen bestimmen''': Wir berechnen nun das Volumen des optimalen Paketes, indem wir <math>60 * 60 * 120 </math> berechnen. | ||
Das maximale Volumen beträgt also <math>432 000 | Das maximale Volumen beträgt also <math>432 000</math>cm³. | ||
|2 = Lösung der Aufgabe | 3= Lösung verbergen}} | |2 = Lösung der Aufgabe | 3= Lösung verbergen}} | ||
Version vom 27. Mai 2020, 12:56 Uhr
Einführung: Optimierungsprobleme
Vorgehen beim Lösen von Optimierungsproblemen
Globales Extremum und Randextremum
Optimierungsprobleme & Funktionenscharen