Digitale Werkzeuge in der Schule/Basiswissen Analysis/Steckbriefaufgaben: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 215: | Zeile 215: | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&\textrm{notwendige} \, \textrm{Bedingung:}& p'(t) &=& 0 \\ | &\textrm{notwendige} \, \textrm{Bedingung:}& p'(t) &=& 0 \\ | ||
&\textrm{hinreichende} \, \textrm{Bedingung:}& p'(t) &=& 0 \, \textrm{und} p''(t) &<& 0 \\ | &\textrm{hinreichende} \, \textrm{Bedingung:}& p'(t) &=& 0 \, \textrm{und} \, p''(t) &<& 0 \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 416: | Zeile 416: | ||
|Farbe= #F19E4F|3= Arbeitsmethode}} | |Farbe= #F19E4F|3= Arbeitsmethode}} | ||
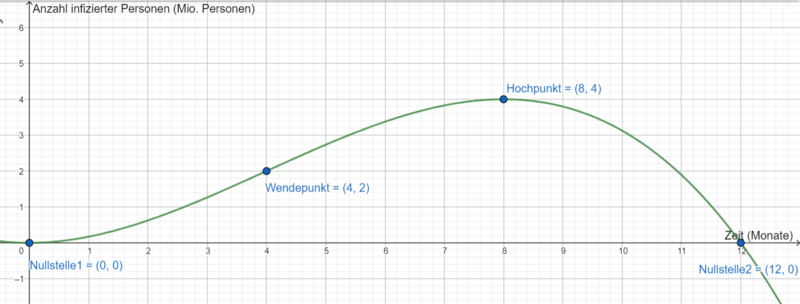
===Kubische Funktionen im Sachzusammenhang=== | ===Kubische Funktionen im Sachzusammenhang=== | ||
| Zeile 436: | Zeile 440: | ||
a) Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion (Funktion dritten Grades) der Form <math> | a) Die Anzahl infizierter Personen lässt sich durch eine kubische Funktion (Funktion dritten Grades) der Form <math>i(t) = at^3 + bt^2 + ct + d</math> beschreiben. Löse zunächst unteren Lückentext. | ||
| Zeile 443: | Zeile 447: | ||
b) Stelle mit Hilfe von Aufgabe a) die Gleichung von <math> | b) Stelle mit Hilfe von Aufgabe a) die Gleichung von <math>i</math> auf. Mit unterem Applet kannst du dein Ergebnis selbstständig überprüfen. | ||
| Zeile 450: | Zeile 454: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math>i(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2)</math> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
i(t) &=& at^3 + bt^2 + ct + d \\ | |||
i'(t) &=& 3at^2 + 2bt + c \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 463: | Zeile 467: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(0) &=& 0 \\ | ||
&\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ | &\Leftrightarrow& a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &=& 0 \\ | ||
&\Leftrightarrow& d &=& 0 \\ | &\Leftrightarrow& d &=& 0 \\ | ||
| Zeile 471: | Zeile 475: | ||
<br /><br /> | <br /><br /> | ||
<math> | <math> | ||
\Rightarrow | \Rightarrow i(t) = at^3 + bt^2 + ct | ||
</math> | </math> | ||
<br /><br /> | <br /><br /> | ||
| Zeile 477: | Zeile 481: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(4) &=& 2 \\ | ||
&\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ | &\Leftrightarrow& a \cdot 4^3 + b \cdot 4^2 + c \cdot 4 &=& 2 \\ | ||
&\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ | &\Leftrightarrow& 64a + 16b + 4c &=& 2 \\ | ||
| Zeile 486: | Zeile 490: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i(8) &=& 4 \\ | ||
&\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ | &\Leftrightarrow& a \cdot 8^3 + b \cdot 8^2 + c \cdot 8 &=& 4 \\ | ||
&\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ | &\Leftrightarrow& 512a + 64b + 8c &=& 4 \\ | ||
| Zeile 495: | Zeile 499: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&& | &&i'(8) &=& 0 \\ | ||
&\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ | &\Leftrightarrow& 3a \cdot 8^2 + 2b \cdot 8 + c &=& 0 \\ | ||
&\Leftrightarrow& 192a + 16b + c &=& 0 \\ | &\Leftrightarrow& 192a + 16b + c &=& 0 \\ | ||
| Zeile 584: | Zeile 588: | ||
<br /><br /> | <br /><br /> | ||
<math> | <math> | ||
i(t) = -\frac{1}{64} t^3 + \frac{3}{16} t^2 = \frac{1}{64} (-t^3 + 12t^2) | |||
</math> | </math> | ||
|2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | |2=Möglicher Lösungsweg|3=Möglichen Lösungsweg ausblenden}} | ||
| Zeile 598: | Zeile 602: | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
&\textrm{notwendige} \, \textrm{Bedingung:}& | &\textrm{notwendige} \, \textrm{Bedingung:}& i''(t) &=& 0 \\ | ||
&\textrm{hinreichende} \, \textrm{Bedingung:}& | &\textrm{hinreichende} \, \textrm{Bedingung:}& i''(t) &=& 0 \, \textrm{und} \, i'''(t) &\neq& 0 \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 605: | Zeile 609: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Graph der Funktion <math> | Der Graph der Funktion <math>i</math> hat einen '''Wendepunkt bei <math>t = 4</math>'''. Die stärkste Zunahme infizierter Personen ist also im April (bzw. im Frühling) nachzuweisen. Die Behauptung ist demnach richtig. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math> | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
i(t) &=& -\frac{1}{64} t^3 + \frac{3}{16} t^2 \\ | |||
i'(t) &=& -\frac{3}{64} t^2 + \frac{3}{8} t \\ | |||
i''(t) &=& -\frac{3}{32} t + \frac{3}{8} \\ | |||
i'''(t) &=& -\frac{3}{32} \\ | |||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 621: | Zeile 625: | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\textrm{Notwendige} \, \textrm{Bedingung:} | \textrm{Notwendige} \, \textrm{Bedingung:} | ||
&& | && i''(t) &=& 0 \\ | ||
&\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ | &\Leftrightarrow& -\frac{3}{32} t + \frac{3}{8} &=& 0 &\mid +\frac{3}{32} t\\ | ||
&\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ | &\Leftrightarrow& \frac{3}{32} t &=& \frac{3}{8} &\mid :\frac{3}{32} \\ | ||
| Zeile 632: | Zeile 636: | ||
\begin{array}{rlll} | \begin{array}{rlll} | ||
\textrm{Hinreichende} \, \textrm{Bedingung:} | \textrm{Hinreichende} \, \textrm{Bedingung:} | ||
&& | &&i''(4) &=& 0 &&\textrm{und} \\ | ||
&& | &&i'''(4) &=& -\frac{3}{32} &\neq& 0 | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 642: | Zeile 646: | ||
d) Skizziere nun den Graphen von <math> | d) Skizziere nun den Graphen von <math>i</math> anhand der Informationen auf einem Blatt. Beachte hierbei die geeignete Beschriftung der Koordinatenachsen. Für welchen Zeitraum ist dieser Graph als mathematische Modellierung der Virusinfektion geeignet? | ||
{{Lösung versteckt|1=[[Datei:Graph e.png|zentriert|rahmenlos|800x800px]] | {{Lösung versteckt|1=[[Datei:Graph e.png|zentriert|rahmenlos|800x800px]] | ||
<br /><br /> | <br /><br /> | ||
Da die Funktionswerte von <math> | Da die Funktionswerte von <math>i</math> für <math>t > 12</math> negativ sind, ist der Graph nur für <math>0 \leq t \leq 12</math> als mathematische Modellierung der Virusinfektion geeignet. Inwiefern der Graph für das vorherige Jahr geeignet ist, lässt sich anhand der Informationen nicht eindeutig feststellen. Der Graph zeigt jedoch, dass zu einem bestimmten Zeitpunkt vor dem beobachteten Jahr unendlich viele infizierte Personen in Deutschland leben, was offensichtlich nicht möglich ist.|2=Lösung|3=Lösung ausblenden}} | ||
|Farbe= #89C64A|3= Arbeitsmethode}} | |Farbe= #89C64A|3= Arbeitsmethode}} | ||
Version vom 26. Mai 2020, 12:12 Uhr
Das Einsetzungsverfahren
Aufgaben zum Einsetzungsverfahren
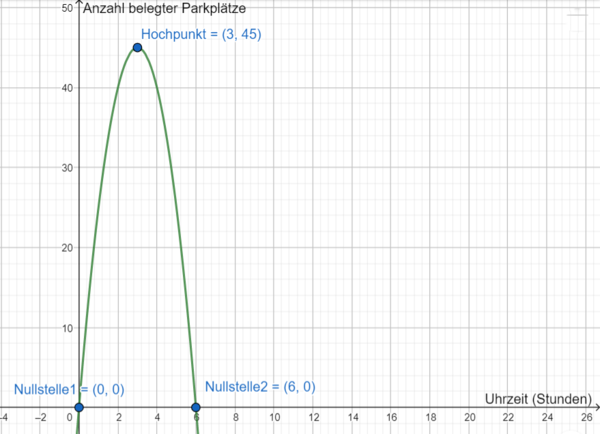
Quadratische Funktionen im Sachzusammenhang
Das Gauß-Verfahren
Aufgaben zum Gauß-Verfahren